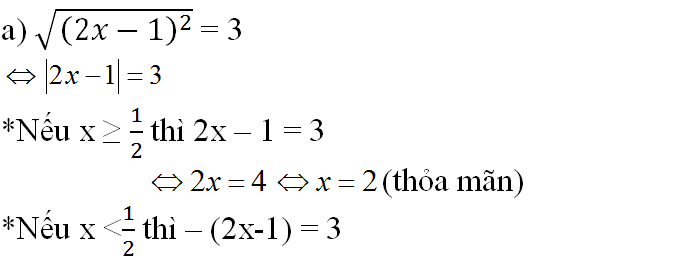\(ĐK:x\ge0\\ PT\Leftrightarrow\dfrac{2}{3}\sqrt{15x}-\dfrac{1}{3}\sqrt{15x}=2\\ \Leftrightarrow\dfrac{1}{3}\sqrt{15x}=2\Leftrightarrow\sqrt{15x}=6\\ \Leftrightarrow15x=36\Leftrightarrow x=\dfrac{12}{5}\left(tm\right)\)

pt j ạ

Đặt \(\sqrt{15x}=a\)

Pt sẽ là \(\dfrac{5}{3a}-a+11=\dfrac{1}{3a}\)

=>\(\dfrac{4}{3a}=a-11\)

\(\Leftrightarrow3a^2-33a-4=0\)

=>\(a=11.12\)

=>căn 15x=11,12

=>15x=123,6544

hay \(x\simeq8,24\)

a) \(\sqrt{\left(2x-1\right)^2}=3\)

\(\Leftrightarrow\left|2x-1\right|=3\)

\(\Leftrightarrow\left[{}\begin{matrix}2x-1=3\\2x-1=-3\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}2x=4\\2x=-2\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)

b) \(\dfrac{5}{3}\sqrt{15x}-\sqrt{15x}-2=\dfrac{1}{3}\sqrt{15x}\)

\(\Leftrightarrow\dfrac{5}{3}\sqrt{15x}-\sqrt{15x}-\dfrac{1}{3}\sqrt{15x}=2\)

\(\Leftrightarrow\dfrac{1}{3}\sqrt{15x}=2\)

\(\Leftrightarrow\sqrt{15x}=6\)

\(\Leftrightarrow15x=6^2\Leftrightarrow15x=36\)

\(\Rightarrow x=\dfrac{5}{12}\)

\(\sqrt{16x+16}-\sqrt{9x+9}+\sqrt{4x+4}+\sqrt{x+1}=16\)

\(\Leftrightarrow4\sqrt{x+1}-3\sqrt{x+1}+2\sqrt{x+1}+\sqrt{x+1}=16\)

\(\Leftrightarrow4\sqrt{x+1}=16\)

\(\Leftrightarrow\sqrt{x+1}=4\)

<=> x + 1 = 16

<=> x = 15 (nhận)

~ ~ ~

\(\sqrt{4x+20}-3\sqrt{5+x}+\dfrac{4}{3}\sqrt{9x+45}=6\)

\(\Leftrightarrow2\sqrt{x+5}-3\sqrt{x+5}+4\sqrt{x+5}=6\)

\(\Leftrightarrow3\sqrt{x+5}=6\)

\(\Leftrightarrow\sqrt{x+5}=2\)

<=> x + 5 = 4

<=> x = - 1 (nhận)

tính tan40°×tan45°×tan50°
#Help me -.-

chắc bạn chép sai đề rồi , hai căn đầu phải 1 cộng 1 trừ chứ

Đặt

\(x=\dfrac{y+1}{2}\Rightarrow y=2x-1\)

\(\Rightarrow y=\sqrt[3]{4+\sqrt{15}}+\sqrt[3]{4-\sqrt{15}}\)

\(y^3=8+3\sqrt[3]{\left(4-\sqrt{15}\right)\left(4+\sqrt{15}\right)}=8+3y\)

\(\Rightarrow y^3-3y-8=0\\ \)

\(\Leftrightarrow8x^3-12x^2-6=0\)

\(\Rightarrow4x^3-6x^2-3=0\)

thay p vào ta có

\(P=12x^5-18x^4+4x^3-15x^2-21\)

\(=12x^5-18x^4-9x^2-4x^3-6x^2-21\)

\(=3x^2\left(4x^2-6x^2-3\right)+4x^3-6x^2-3\\ =3x^2.0+0-18\\ =-18\)

\(M=\sqrt{15x^2-8x\sqrt{15+16}}\)

\(\Leftrightarrow M=\sqrt{\left(\sqrt{15}.x+4\right)^2}=\left|\sqrt{15}.x+4\right|=\sqrt{15}.x+4\)

Thay \(x=\sqrt{\dfrac{3}{5}}+\sqrt{\dfrac{5}{3}}\) vào BT ta được:

\(M=\sqrt{15}.\left(\sqrt{\dfrac{3}{5}}+\sqrt{\dfrac{5}{3}}\right)+4=\sqrt{9}+\sqrt{25}+4=3+5+4=12\)

Vậy \(M=12\)

\(a=\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt{1+\dfrac{1}{x^2}}+1}{\dfrac{5}{x}-2}=\dfrac{1+1}{-2}=-1\)

Câu b bạn coi lại đề, số cuối là \(-3\) hay \(-7\) nhỉ? 

Kí hiệu lim làm theo thứ tự này:

Câu b số cuối là -3 thì nó hơi kì quặc (vì không phải dạng vô định, cứ thay số thôi):

\(=\lim\limits_{x\rightarrow4}\dfrac{\sqrt{15.4+4}-\sqrt{4-3}-3}{-4+4}=\dfrac{4}{0}=+\infty\)

3.

Ta có: \(VT=\)\(8+2\sqrt{10+2\sqrt{5}}+8-2\sqrt{10+2\sqrt{5}}\)

\(=8+8+\left(2\sqrt{10+2\sqrt{5}}-2\sqrt{10+2\sqrt{5}}\right)\)

\(=16\ne VP\)

⇒ Đề sai

1. Ta có: \(\sqrt{4x}\)- 3\(\sqrt{x}\)+2\(\sqrt{15x}\)=18

⇌2\(\sqrt{x}\)-3\(\sqrt{x}\) +2\(\sqrt{15x}\)=18

⇌\(-\sqrt{x}\) +2\(\sqrt{15x}\)-15 = 3

⇌-(\(\sqrt{x}\) -2\(\sqrt{15x}\)+15 )=3

⇌(\(\sqrt{x}\)-\(\sqrt{15}\))=-3 (vô lí)

Vậy không tìm được giá trị x thỏa mãn bài toán

2.Ta có: B=\(\dfrac{1}{\sqrt{11-2\sqrt{30}}}-\dfrac{3}{7-2\sqrt{10}}\)

= \(\dfrac{1}{\sqrt{6-2\sqrt{6.5}+5}}-\dfrac{3}{2-2\sqrt{2.5}+5}\)

=\(\dfrac{1}{\sqrt{\left(\sqrt{6}-\sqrt{5}\right)^2}}-\dfrac{3}{\left(\sqrt{3}-\sqrt{2}\right)^2}\)

=\(\dfrac{1}{\sqrt{6}-\sqrt{5}}-\dfrac{3}{\sqrt{3}-\sqrt{2}}\)

hình như đề sai