Cho a,b,c>0 tm \(a^2+b^2+c^2+abc=4\).CMR:
\(a+b+c\ge\Sigma a\sqrt{bc}\)
Những câu hỏi liên quan
ten ten ten1. Cho a,b,c0 và a+b+c1 CMR sigmafrac{a-bc}{a+bc}lefrac{3}{2}2. cho a,b,c0 va abc1 CMR sigmafrac{1}{aleft(b+1right)}gefrac{3}{2}3.(i think it is difficult for you)ch a,b,c0 CMR sigmafrac{b^2c^3}{a^2+left(b+cright)^3}gefrac{9abc}{4left(3abc+ab^2+bc^2+ca^2right)}4. CMR với mọi n là số tự nhiên lớn hơn 1 thì frac{1}{sqrt{n^2+1}}+frac{1}{sqrt{n^2+2}}+...+frac{1}{sqrt{n^2+n}} 1
Đọc tiếp
ten ten ten
1. Cho a,b,c>0 và a+b+c=1 CMR sigma\(\frac{a-bc}{a+bc}\le\frac{3}{2}\)
2. cho a,b,c>0 va abc=1 CMR sigma\(\frac{1}{a\left(b+1\right)}\ge\frac{3}{2}\)
3.(i think it is difficult for you)
ch a,b,c>0 CMR sigma\(\frac{b^2c^3}{a^2+\left(b+c\right)^3}\ge\frac{9abc}{4\left(3abc+ab^2+bc^2+ca^2\right)}\)
4. CMR với mọi n là số tự nhiên lớn hơn 1 thì \(\frac{1}{\sqrt{n^2+1}}+\frac{1}{\sqrt{n^2+2}}+...+\frac{1}{\sqrt{n^2+n}}< 1\)
bài 1
<=> \(\frac{bc}{a\left(a+b+c\right)+bc}\)
sử dụng tiếp cauchy sharws
Bài 2: đặt a=x/y, b=y/x, c=z/x
Đúng 0
Bình luận (0)
1. a,b,c0 và a+b+c2017CM:Sigmadfrac{2017a-a^2}{bc}gesqrt{2}left(Sigmasqrt{dfrac{2017-a}{a}}right)2. cho x,y,z tm: x^2+y^2+z^23CM:8left(2-xright)left(2-yright)left(2-zright)geleft(x+yzright)left(y+zxright)left(z+xyright)3. a,b,c0 và a^2+b^2+c^2ge6CM:Sigmadfrac{1}{1+ab}gedfrac{3}{2}
Đọc tiếp
1. a,b,c>0 và a+b+c=2017
\(CM:\Sigma\dfrac{2017a-a^2}{bc}\ge\sqrt{2}\left(\Sigma\sqrt{\dfrac{2017-a}{a}}\right)\)
2. cho x,y,z tm: \(x^2+y^2+z^2=3\)
\(CM:8\left(2-x\right)\left(2-y\right)\left(2-z\right)\ge\left(x+yz\right)\left(y+zx\right)\left(z+xy\right)\)
3. a,b,c>0 và \(a^2+b^2+c^2\ge6\)
\(CM:\Sigma\dfrac{1}{1+ab}\ge\dfrac{3}{2}\)
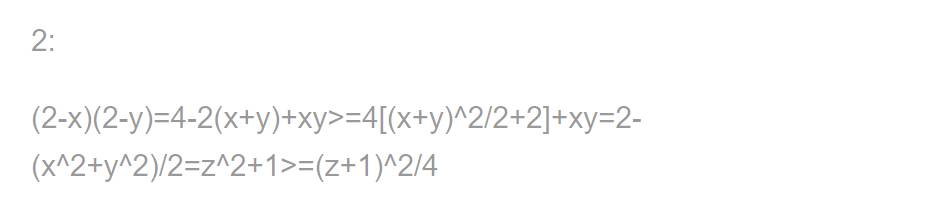
Tương tự, ta được:
\(\left(2-y\right)\left(2-z\right)>=\dfrac{\left(x+1\right)^2}{4}\)
và \(\left(2-z\right)\left(2-x\right)>=\left(\dfrac{y+1}{2}\right)^2\)
=>8(2-x)(2-y)(2-z)>=(x+1)(y+1)(z+1)
(x+yz)(y+zx)<=(x+y+yz+xz)^2/4=(x+y)^2*(z+1)^2/4<=(x^2+y^2)(z+1)^2/4
Tương tự, ta cũng co:
\(\left(y+xz\right)\left(z+y\right)< =\dfrac{\left(y^2+z^2\right)\left(x+1\right)^2}{2}\)
và \(\left(z+xy\right)\left(x+yz\right)< =\dfrac{\left(z^2+x^2\right)\left(y+1\right)^2}{2}\)
Do đó, ta được:
\(\left(x+yz\right)\left(y+zx\right)\left(z+xy\right)< =\left(x+1\right)\left(y+1\right)\left(z+1\right)\)
=>ĐPCM
Đúng 0
Bình luận (0)
1) Cho a,b,c0 tm a+b+c3. Cmr frac{1}{2+a^2+b^2}+frac{1}{2+b^2+c^2}+frac{1}{2+c^2+a^2}lefrac{3}{4}2) Cho a,b,c0 tm a^2+b^2+c^2le abc.Cmr frac{a}{a^2+bc}+frac{b}{b^2+ca}+frac{c}{c^2+ab}lefrac{1}{2}3) Cho a,b,c0 tm sqrt{a}+sqrt{b}+sqrt{c}1.Cmr sqrt{frac{ab}{a+b+2c}}+sqrt{frac{bc}{b+c+2a}}+sqrt{frac{ca}{c+a+2b}}lefrac{1}{2}Giúp mình mới nhé các bạn. Mình đang cần gấp
Đọc tiếp
1) Cho a,b,c>0 tm a+b+c=3. Cmr \(\frac{1}{2+a^2+b^2}+\frac{1}{2+b^2+c^2}+\frac{1}{2+c^2+a^2}\le\frac{3}{4}\)
2) Cho a,b,c>0 tm \(a^2+b^2+c^2\le abc\).Cmr \(\frac{a}{a^2+bc}+\frac{b}{b^2+ca}+\frac{c}{c^2+ab}\le\frac{1}{2}\)
3) Cho a,b,c>0 tm \(\sqrt{a}+\sqrt{b}+\sqrt{c}=1\).Cmr \(\sqrt{\frac{ab}{a+b+2c}}+\sqrt{\frac{bc}{b+c+2a}}+\sqrt{\frac{ca}{c+a+2b}}\le\frac{1}{2}\)
Giúp mình mới nhé các bạn. Mình đang cần gấp
6 tháng 1 2023 lúc 21:33
cho:\(\left\{{}\begin{matrix}a,b,c>0\\a+b+c=3\end{matrix}\right.\)
CMR: \(A=\Sigma\dfrac{1}{5a^2+ab+bc}\ge\dfrac{3}{7}\)
27 tháng 8 2021 lúc 10:49
$\rm Cho\ a,b,c \ge 0 .Thoả \ mãn \ ab+bc+ac=abc .Chứng \ minh\ a^{2}+b^{2}+c^{2}+5abc \ge 8$
`b)` Cho` a,b,c>=0,ab+bc+ca+abc=4`
CMR:`a^2+b^2+c^2+5abc>=8`
a. Đề bài sai (thực chất là nó đúng 1 cách hiển nhiên nhưng "dạng" thế này nó sai sai vì ko ai cho kiểu này cả)
Ta có: \(abc=ab+bc+ca\ge3\sqrt[3]{a^2b^2c^2}\Rightarrow abc\ge27\)
\(\Rightarrow a^2+b^2+c^2+5abc\ge a^2+b^2+c^2+5.27>>>>>8\)
b.
\(4=ab+bc+ca+abc=ab+bc+ca+\sqrt{ab.bc.ca}\le ab+bc+ca+\sqrt{\left(\dfrac{ab+bc+ca}{3}\right)^3}\)
\(\sqrt{\dfrac{ab+bc+ca}{3}}=t\Rightarrow t^3+3t^2-4\ge0\Rightarrow\left(t-1\right)\left(t+2\right)^2\ge0\)
\(\Rightarrow t\ge1\Rightarrow ab+bc+ca\ge3\Rightarrow a+b+c\ge\sqrt{3\left(ab+bc+ca\right)}\ge3\)
- TH1: nếu \(a+b+c\ge4\)
Ta có: \(ab+bc+ca=4-abc\le4\)
\(\Rightarrow P=\left(a+b+c\right)^2-2\left(ab+bc+ca\right)+5abc\ge4^2-2.4+0=8\)
(Dấu "=" xảy ra khi \(\left(a;b;c\right)=\left(2;2;0\right)\) và các hoán vị)
- TH2: nếu \(3\le a+b+c< 4\)
Đặt \(a+b+c=p\ge3;ab+bc+ca=q;abc=r\)
\(P=p^2-2q+5r=p^2-2q+5\left(4-q\right)=p^2-7q+20\)
Áp dụng BĐT Schur:
\(4=q+r\ge q+\dfrac{p\left(4q-p^2\right)}{9}\Leftrightarrow q\le\dfrac{p^3+36}{4p+9}\)
\(\Rightarrow P\ge p^2-\dfrac{7\left(p^3+36\right)}{4p+9}+20=\dfrac{3\left(4-p\right)\left(p-3\right)\left(p+4\right)}{4p+9}+8\ge8\)
(Dấu "=" xảy ra khi \(a=b=c=1\))
Đúng 1
Bình luận (0)
a) Cho a , b > 0 CMR : 3(b2+2a2) ≥ (b+2a)2
b) Cho a,b,c > 0 thõa mãn ab+bc+ca = abc
CMR : \(\dfrac{\sqrt{b^2+2a^2}}{ab}+\dfrac{\sqrt{c^2+2b^2}}{bc}+\dfrac{\sqrt{a^2+2c^2}}{ca}\ge\sqrt{3}\)
a)Bunhia:
\(\left(1+2\right)\left(b^2+2a^2\right)\ge\left(1.b+\sqrt{2}.\sqrt{2}a\right)^2=\left(b+2a\right)^2\)
b)\(ab+bc+ca=abc\Leftrightarrow\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}=1\)
Áp dụng bđt câu a
=>VT\(\ge\)\(\dfrac{b+2a}{\sqrt{3}ab}+\dfrac{c+2b}{\sqrt{3}bc}+\dfrac{a+2c}{\sqrt{3}ca}\)
\(\Leftrightarrow VT\ge\dfrac{1}{a}+\dfrac{2}{b}+\dfrac{1}{b}+\dfrac{2}{c}+\dfrac{1}{c}+\dfrac{2}{a}=3=VP\)
Tự tìm dấu "="
Đúng 0
Bình luận (0)
Cho a,b,c>0 tm: \(\sqrt{a^2+b^2}+\sqrt{b^2+c^2}+ \sqrt{a^2+c^2}=\sqrt{2018}\)
CMR \(\frac{a^2}{b+c}+\frac{b^2}{c+a}+\frac{c^2}{a+b} \ge\frac{1}{2}\sqrt{2009}\)
Đúng 0
Bình luận (0)
1) Cho a,b,c0 tm a+b+c3. Cmr frac{1}{2+a^2+b^2}+frac{1}{2+b^2+c^2}+frac{1}{2+c^2+a^2}lefrac{3}{4}2) Cho a,b,c0 tm a^2+b^2+c^2 bé hơn hoặc bằng abc. Cmr frac{a}{a^2+bc}+frac{b}{b^2+ca}+frac{c}{c^2+ab}lefrac{1}{2}3) Cho a,b,c0 tm a+b+c3. Cmr frac{ab}{sqrt{3+c}}+frac{bc}{sqrt{3+a}}+frac{ca}{sqrt{3+b}}lefrac{3}{2}4) Cho a,b,c0 tm a+b+c2. Cmr frac{a}{sqrt{4a+3bc}}+frac{b}{sqrt{4b+3ca}}+frac{c}{sqrt{4c+3ab}}le15) Cho a,b,c0. Cmr sqrt{frac{a^3}{5a^2+left(b+cright)^2}}+sqrt{frac{b^3}{5b^2+left(c+aright)...
Đọc tiếp
1) Cho a,b,c>0 tm a+b+c=3. Cmr \(\frac{1}{2+a^2+b^2}+\frac{1}{2+b^2+c^2}+\frac{1}{2+c^2+a^2}\le\frac{3}{4}\)
2) Cho a,b,c>0 tm a^2+b^2+c^2 bé hơn hoặc bằng abc. Cmr \(\frac{a}{a^2+bc}+\frac{b}{b^2+ca}+\frac{c}{c^2+ab}\le\frac{1}{2}\)
3) Cho a,b,c>0 tm a+b+c<=3. Cmr \(\frac{ab}{\sqrt{3+c}}+\frac{bc}{\sqrt{3+a}}+\frac{ca}{\sqrt{3+b}}\le\frac{3}{2}\)
4) Cho a,b,c>0 tm a+b+c=2. Cmr \(\frac{a}{\sqrt{4a+3bc}}+\frac{b}{\sqrt{4b+3ca}}+\frac{c}{\sqrt{4c+3ab}}\le1\)
5) Cho a,b,c>0. Cmr \(\sqrt{\frac{a^3}{5a^2+\left(b+c\right)^2}}+\sqrt{\frac{b^3}{5b^2+\left(c+a\right)^2}}+\sqrt{\frac{c^3}{5c^2+\left(a+b\right)^2}}\le\sqrt{\frac{a+b+c}{3}}\)
6) Cho a,b,c>0. Cmr \(\frac{a^2}{\left(2a+b\right)\left(2a+c\right)}+\frac{b^2}{\left(2b+a\right)\left(2b+c\right)}+\frac{c^2}{\left(2c+a\right)\left(2c+b\right)}\le\frac{1}{3}\)
Giúp mình với nhé các bạn
Bai 1:Cho a,b,c>0 CMR
\(|\Sigma \frac{a^3-b^3}{a+b}| \leq \frac{\Sigma(a-b)^2}{4}\)
Bai 2 :Cho \(a,b,c \in R\) CMR
\(\Sigma \sqrt{a^2+(1-b)^2} \geq \frac{3}{\sqrt{2}}\)
Cm \(3\left(a^2b+b^2c+c^2a\right)\left(a^2c+b^2a+c^2b\right)\ge abc\left(a+b+c\right)^3\)
Do 2 vế BĐT đồng bậc nên ta chuẩn hóa \(a+b+c=3\)
BĐT <=> \(3\left[abc\left(a^3+b^3+c^3\right)+\left(a^3b^3+b^3c^3+a^3c^3\right)+a^2b^2c^2\left(a+b+c\right)\right]\ge27abc\)
<=>\(3\left[abc\left(a^3+b^3+c^3\right)+\left(a^3b^3+b^3c^3+a^3c^3+3a^2b^2c^2\right)\right]\ge27abc\)
Áp dụng BĐT Schur ta có:
\(a^3b^3+b^3c^3+a^3c^3+3a^2b^2c^2\ge ab^2c\left(ab+bc\right)+a^2bc\left(ab+ac\right)+abc^2\left(ac+bc\right)\)
Khi đó BĐT
<=>\(3\left(a^3+b^3+c^3\right)+3a^2\left(b+c\right)+3b^2\left(a+c\right)+3c^2\left(a+b\right)\ge27\)
<=> \(3\left(a^3+b^3+c^3\right)+3a^2\left(3-a\right)+3b^2\left(3-b\right)+3c^2\left(3-c\right)\ge27\)
<=> \(a^2+b^2+c^2\ge3\) luôn đúng do \(a^2+b^2+c^2\ge\frac{1}{3}\left(a+b+c\right)^2=3\)( ĐPCM)
Dấu bằng xảy ra khi a=b=c
Bài 2
Áp dụng \(x^2+y^2\ge\frac{\left(x+y\right)^2}{2}\)
=> \(VT\ge\frac{|a+1-b|+|b+1-c|+|c+1-a|}{\sqrt{2}}\)
Áp dụng BĐT \(|x|+|y|+|z|\ge|x+y+z|\)
=> \(VT\ge\frac{|a+1-b+b+1-c+c+1-a|}{\sqrt{2}}=\frac{3}{\sqrt{2}}\)(ĐPCM)
Dấu bằng xảy ra khi \(a=b=c=\frac{1}{2}\)