1. a,b,c>0 và a+b+c=2017
\(CM:\Sigma\dfrac{2017a-a^2}{bc}\ge\sqrt{2}\left(\Sigma\sqrt{\dfrac{2017-a}{a}}\right)\)
2. cho x,y,z tm: \(x^2+y^2+z^2=3\)
\(CM:8\left(2-x\right)\left(2-y\right)\left(2-z\right)\ge\left(x+yz\right)\left(y+zx\right)\left(z+xy\right)\)
3. a,b,c>0 và \(a^2+b^2+c^2\ge6\)
\(CM:\Sigma\dfrac{1}{1+ab}\ge\dfrac{3}{2}\)
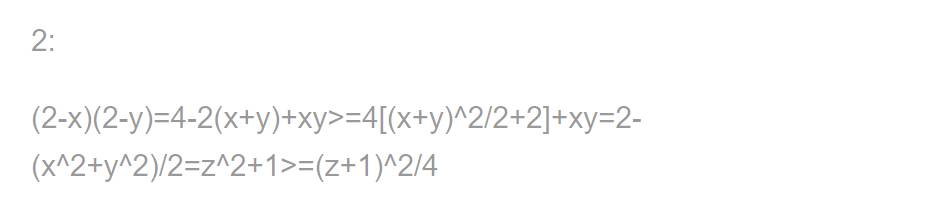
Tương tự, ta được:
\(\left(2-y\right)\left(2-z\right)>=\dfrac{\left(x+1\right)^2}{4}\)
và \(\left(2-z\right)\left(2-x\right)>=\left(\dfrac{y+1}{2}\right)^2\)
=>8(2-x)(2-y)(2-z)>=(x+1)(y+1)(z+1)
(x+yz)(y+zx)<=(x+y+yz+xz)^2/4=(x+y)^2*(z+1)^2/4<=(x^2+y^2)(z+1)^2/4
Tương tự, ta cũng co:
\(\left(y+xz\right)\left(z+y\right)< =\dfrac{\left(y^2+z^2\right)\left(x+1\right)^2}{2}\)
và \(\left(z+xy\right)\left(x+yz\right)< =\dfrac{\left(z^2+x^2\right)\left(y+1\right)^2}{2}\)
Do đó, ta được:
\(\left(x+yz\right)\left(y+zx\right)\left(z+xy\right)< =\left(x+1\right)\left(y+1\right)\left(z+1\right)\)
=>ĐPCM










