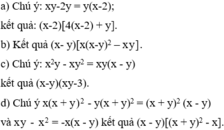Tính x(x−y)2−y(x−y)2+xy2−x2y biết x - y = 9 và xy = 9

Những câu hỏi liên quan
Đa thức �2�+��2−�−�x2y+xy2−x−y được phân tích thành nhân tử là
(�−�)(��−1)(x−y)(xy−1).
(�−�)(��+1)(x−y)(xy+1).
(�+�)(��+1)(x+y)(xy+1).
(�+�)(��−1)(x+y)(xy−1)
Đọc tiếp
Đa thức được phân tích thành nhân tử là
. . .x²y + xy² - x - y
= (x²y + xy²) - (x + y)
= xy(x + y) - (x + y)
= (x + y)(xy - 1)
Đúng 2
Bình luận (0)
Bài 2:Phân tích đa thức thành nhân tử chung
a, 4(2-x)2+xy-2y
b, x(x-y)3-y(y-x)2-y2(x-y)
c, x2y-xy2-3x+3y
d, x(x+y)2-y(x+y2)+xy-x2
a) \(4\left(2-x\right)^2+xy-2y\)
\(=4\left(x-2\right)^2+\left(xy-2y\right)\)
\(=4\left(x-2\right)\left(x-2\right)+y\left(x-2\right)\)
\(=\left(x-2\right)\left(4x-8\right)+y\left(x-2\right)\)
\(=\left(x-2\right)\left(4x-8+x-2\right)\)
\(=\left(x-2\right)\left(5x-10\right)\)
\(=5\left(x-2\right)^2\)
Đúng 1
Bình luận (1)
a, \(=4\left(x-2\right)^2+y\left(x-2\right)=\left(x-2\right)\left(4x-8+y\right)\)
b, \(=x\left(x-y\right)^3-y\left(x-y\right)^2-y^2\left(x-y\right)=\left(x-y\right)\left[x\left(x-y\right)^2-y\left(x-y\right)-y^2\right]=\left(x-y\right)\left[x\left(x^2-2xy+y^2\right)-xy+y^2-y^2\right]=\left(x-y\right)\left(x^3-2x^2y+xy^2-xy\right)=x\left(x-y\right)\left(x^2-2xy+y^2-y\right)\)
c, \(=xy\left(x-y\right)-3\left(x-y\right)=\left(xy-3\right)\left(x-y\right)\)
d, không phân tích được
Đúng 1
Bình luận (1)
c, x2y - xy2 - 3x + 3y
= xy(x-y) - 3(x-y)
= (x-y)(x-3)
Đúng 0
Bình luận (0)
Phân tích đa thức thành nhân tử:a) 4
(
2
-
x
)
2
+ xy - 2y;b) x
(
x
-
y
)
3
-
y
(
y
-
...
Đọc tiếp
Phân tích đa thức thành nhân tử:
a) 4 ( 2 - x ) 2 + xy - 2y;
b) x ( x - y ) 3 - y ( y - x ) 2 - y 2 (x - y);
c) x 2 y - xy 2 - 3x + 3y;
d) x ( x + y ) 2 - y ( x + y ) 2 + xy - x 2
Phân tích tử và mẫu thành nhân tử rồi rút gọn phân thức:
a) x2 + xy +x + y / x2 - xy + x - y
b) x2 - 6x+ 9 / 3x2 - 9x
c) y2 - x2 / x2y - xy2
\(a,=\dfrac{\left(x+1\right)\left(x+y\right)}{\left(x-y\right)\left(x+1\right)}=\dfrac{x+y}{x-y}\\ b,=\dfrac{\left(x-3\right)^2}{3x\left(x-3\right)}=\dfrac{x-3}{3x}\\ c,=\dfrac{\left(y-x\right)\left(y+x\right)}{xy\left(x-y\right)}=\dfrac{-x-y}{xy}\)
Đúng 2
Bình luận (0)
Lời giải:
a.
\(\frac{x^2+xy+x+y}{x^2-xy+x-y}=\frac{x(x+y)+(x+y)}{x(x+1)-y(x+1)}=\frac{(x+y)(x+1)}{(x+1)(x-y)}=\frac{x+y}{x-y}\)
b.
\(\frac{x^2-6x+9}{3x^2-9x}=\frac{(x-3)^2}{3x(x-3)}=\frac{x-3}{3x}\)
c.
\(\frac{y^2-x^2}{x^2y-xy^2}=\frac{(y-x)(y+x)}{-xy(y-x)}=\frac{x+y}{-xy}\)
Đúng 1
Bình luận (3)
Tính GT biểu thức
C=xyz-(xy+yz+zx)+x+y+z-1 với x=9; y=10; z=11
D=x3-x2y-xy2+y3 với x=5,75; y=4,25
\(C=xyz+\left(xy+yz+xz\right)+x+y+z-1\)
Ta có ĐT tương đương
\(C=xyz+\left(xy+yz+xz\right)+x+y+z-1=\left(x-1\right)\left(y-1\right)\left(z-1\right)\)
Thay \(x=9\) ; \(y=10\) ; \(z=11\) vào BT có :
\(\left(9-1\right)\left(10-1\right)\left(11-1\right)=720\)
Vậy .........
Đúng 0
Bình luận (0)
C = xyz - xy - yz - xz + x + y +z- 1
= xy(z-1) - y(z-1) - x(z-1) + 1(z-1)
(xy-y-x+1)(z-1)
Đúng 0
Bình luận (0)
Tính giá trị của các biểu thức: x3 + x2y + xy2 + 2xy(x + y)
biết x + y = 2
Đề sai r bn, nếu x,y thay đổi thì tổng biểu thức cũng thay đổi
Đúng 0
Bình luận (0)
Cho 2 số thực dương x,y thỏa mãn
a, x4 + y4 + \(\dfrac{1}{xy}\) = xy + 2
b, x2y + xy2 = x + y + 3xy
Tìm min S = a + b
a, thu gọn đơn thức:1/9 xy.(-3x2 y)3
b, thu gọn rồi tính giá trị đa thức:A=1/3x2 y-xy2+2/3x2 y=1/2 xy+xy2+1 tại x=1,y=-1
a: \(=\dfrac{1}{9}xy\cdot\left(-27\right)x^6y^3=-3x^7y^4\)
b: \(A=\dfrac{1}{3}x^2y-xy^2+\dfrac{2}{3}x^2y+\dfrac{1}{2}xy+xy^2+1\)
=x^2y+1/2xy+1
Khi x=1 và y=-1 thì A=-1-1/2+1=-1/2
Đúng 0
Bình luận (0)
Biết xy = 11 và x2y + xy2 + x + y = 240 . Hãy Tính x3+ y3
\(x^2y+xy^2+x+y=240\)
\(\Leftrightarrow xy\left(x+y\right)+x+y=240\)
\(\Leftrightarrow11\left(x+y\right)+x+y=240\)
\(\Rightarrow12\left(x+y\right)=240\)
\(\Rightarrow x+y=20\)
\(x^3+y^3=\left(x+y\right)^3-3xy\left(x+y\right)=20^3-3.11.20=\)
Đúng 0
Bình luận (0)
E=(x3-x2y+xy2-y3)(x+y) với x=2, y=1/2
Ta có: \(\left(x^3-x^2y+xy^2-y^3\right)\left(x+y\right)\)
\(=\left[x^2\left(x-y\right)+y^2\left(x-y\right)\right]\left(x+y\right)\)
\(=\left(x^2-y^2\right)\left(x^2+y^2\right)\)
\(=x^4-y^4=2^4-\left(\dfrac{1}{2}\right)^4=16-\dfrac{1}{16}=\dfrac{255}{16}\)
Đúng 1
Bình luận (0)