Tính a,b
\(\left\{{}\begin{matrix}2a+b=50\\2a-b=14\end{matrix}\right.\)
\(\left\{{}\begin{matrix}a^3+b^3+ab=2a+4\\ab+a+2b=1\end{matrix}\right.\)
Giải và biện luận hệ phương trình theo a,b
\(\left\{\begin{matrix}\left(a+b\right).x+\left(a-b\right).y=a\\\left(2a+b\right).x+\left(2a-b\right).y=b\end{matrix}\right.\)
Lấy (2)-(1) Và (2)-(1) nhân 2
hệ mới
\(\Leftrightarrow\left\{\begin{matrix}ax+ay=b-a\left(3\right)\\-bx+by=b-2a\left(4\right)\end{matrix}\right.\Leftrightarrow\left\{\begin{matrix}ax+ay=b-a\left(3\right)\\bx-by=2a-b\left(4\right)\end{matrix}\right.\)
Nếu a=0; b=0 nghiệm đúng với mọi x,y
Nếu a=0; b khác 0 => (3) hệ vô nghiệm
nếu b=0; a khác 0 => (4) hệ vô nghiệm
\(a,b\ne0\) hệ mới \(\left\{\begin{matrix}x+y=\frac{b-a}{a}\left(5\right)\\x-y=\frac{2a-b}{b}\left(6\right)\end{matrix}\right.\)
cộng và trừ cho nhau \(\left\{\begin{matrix}2x=\frac{b-a}{a}+\frac{2a-b}{b}\\2y=\frac{b-a}{a}-\frac{2a-b}{b}\end{matrix}\right.\)
\(\Leftrightarrow\left\{\begin{matrix}x=\frac{b^2+2a^2-2ab}{2ab}\\y=\frac{b^2-2a^2}{2ab}\end{matrix}\right.\)
Kết luận:
Với a hoặc b =0 hệ vô nghiệm
Với a và b=0 hệ vô số nghiệm " với mọi x,y"
Với a và b khác 0 hệ có nghiệm duy nhất:\(\left\{\begin{matrix}x=\frac{b^2+2a^2-2ab}{2ab}\\y=\frac{b^2-2a^2}{2ab}\end{matrix}\right.\)
Giải hệ phương trình \(\left\{{}\begin{matrix}2a^3+2a+b^3-3b=62\\a^2+b^2-2a+2b=2\end{matrix}\right.\)
Đây nha bạn trọng :)  :)
:)
giải pt \(\left\{{}\begin{matrix}a+b=\dfrac{5}{6}\\\dfrac{2a}{3}+\dfrac{14b}{9}=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a+b=\dfrac{5}{6}\\\dfrac{6a+14b}{9}=\dfrac{9}{9}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a+b=\dfrac{5}{6}\\6a+14b=9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{5}{6}-b\\6\left(\dfrac{5}{6}-b\right)+14b=9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{5}{6}-b\\5-6b+14b=9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{5}{6}-b\\8b=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{5}{6}-\dfrac{1}{2}=\dfrac{1}{3}\\b=\dfrac{1}{2}\end{matrix}\right.\)
\(\left\{{}\begin{matrix}a+b=\dfrac{5}{6}\\\dfrac{2a}{3}+\dfrac{14b}{9}=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{14a}{9}+\dfrac{14b}{9}=\dfrac{35}{27}\\\dfrac{2a}{3}+\dfrac{14b}{9}=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{8}{9}a=\dfrac{8}{27}\\\dfrac{2a}{3}+\dfrac{14b}{9}=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{1}{3}\\\dfrac{2a}{3}+\dfrac{14b}{9}=1\end{matrix}\right.\)
\(\Leftrightarrow\dfrac{2.\dfrac{1}{3}}{3}+\dfrac{14b}{9}=1\)
\(\Leftrightarrow\dfrac{14b}{9}=1-\dfrac{2}{9}=\dfrac{7}{9}\)
\(\Leftrightarrow b=\dfrac{7}{9}:\dfrac{14}{9}=\dfrac{1}{2}\)
Vậy ...
\(\Leftrightarrow\left\{{}\begin{matrix}a+b=\dfrac{5}{6}\\6a+14b=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}6a+6b=5\\6a+14b=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=\dfrac{1}{2}\\a=\dfrac{1}{3}\end{matrix}\right.\)
1.\(\left\{{}\begin{matrix}a,b>0\\2a+3b=4\end{matrix}\right.\)Tìm GTNN của
M=\(\dfrac{2002}{a}+\dfrac{2017}{b}+2096a-5501b\)
Bài này mình làm lâu rồi á bann sửa dấu `2a+3b<=4` thành `2a+3b=4` nhé!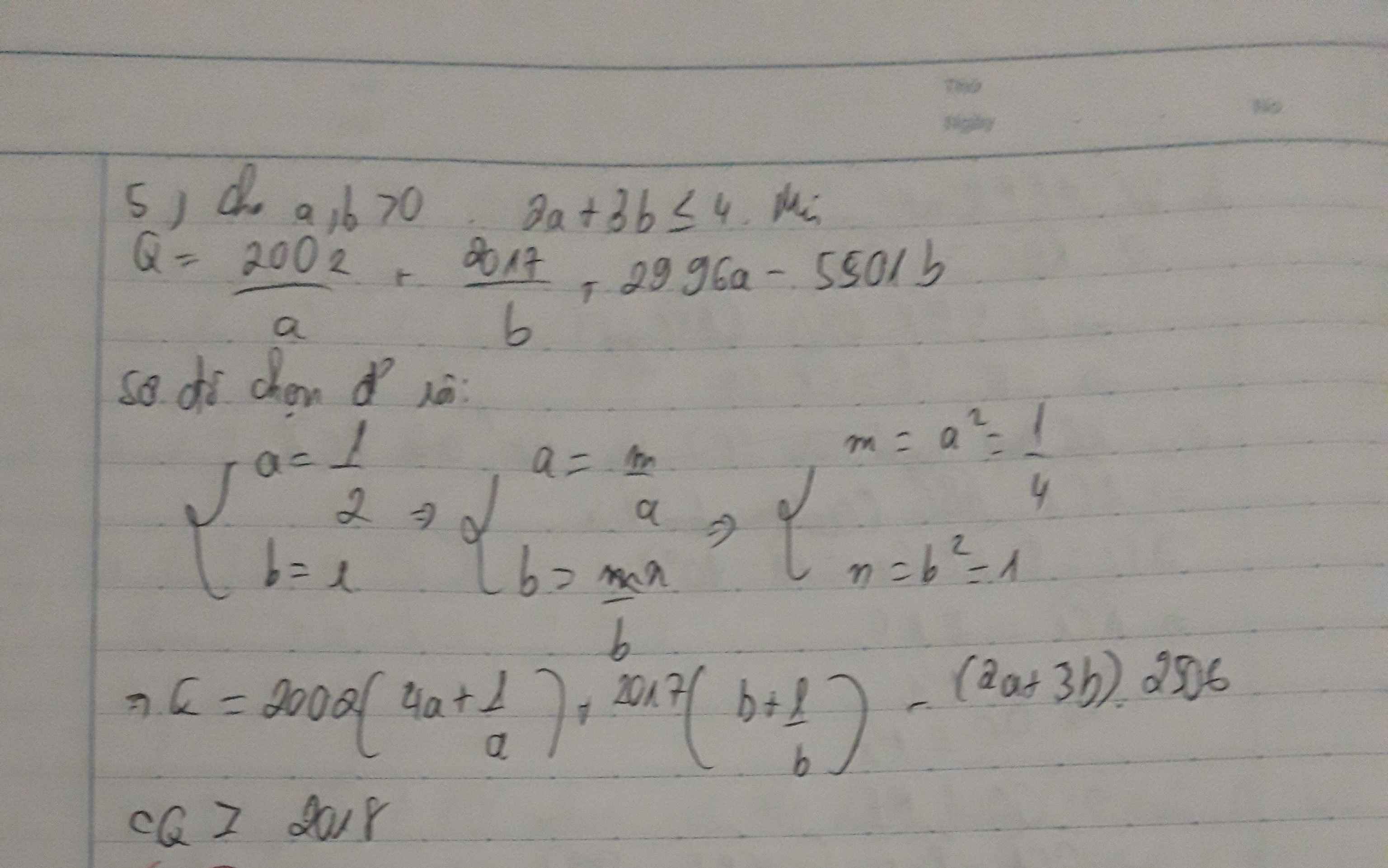
Giải hệ phương trình : \(\left\{{}\begin{matrix}a+b=21\\2a+b=30\end{matrix}\right.\)
C1 : Ta trừ vế với vế :
\(\left(a+b\right)-\left(2a+b\right)=21-30\)
=> a + b - 2a - b = -9
=> -a = -9
=> a = 9
=> b = 21 - 9 =12
C2 : Bấm máy tính ( Đối với máy tính \(fx-570VN\) \(PLUS\) )
B1 : Mode
B2 : Bấm phím 5 ( 5: EQN )
B3 : Bâm phím 1 ( 1: \(anX+bnY=cn\) )
B2 : Nhập hệ số của a ,b ,21,2a,b,30
B5 : Bấm dấu " = "
Tính a,b
\(\left\{{}\begin{matrix}2a+b=82\\15a-13b=0\end{matrix}\right.\)
\(\left\{{}\begin{matrix}a+b=\dfrac{1}{6}\\2a+2b=\dfrac{2}{5}\end{matrix}\right.\)
Ta có:
\(a+b=\dfrac{1}{6}\)
<=> \(a=\dfrac{1}{6}-b\) (*)
Thay (*) vào phương trình 2 ta có:
\(2\left(\dfrac{1}{6}-b\right)+2b=\dfrac{2}{5}\)
<=> \(\dfrac{1}{3}-2b+2b=\dfrac{2}{5}\)
<=> \(\dfrac{1}{3}=\dfrac{2}{5}\) ( vô lí)
Vậy hệ phương trình bậc nhất hai ẩn này vô nghiệm
hệ\(\Leftrightarrow\left\{{}\begin{matrix}a+b=\dfrac{1}{6}\\a+b=\dfrac{1}{5}\end{matrix}\right.\)(vô lí)
\(\Rightarrow\)hệ vô nghiệm