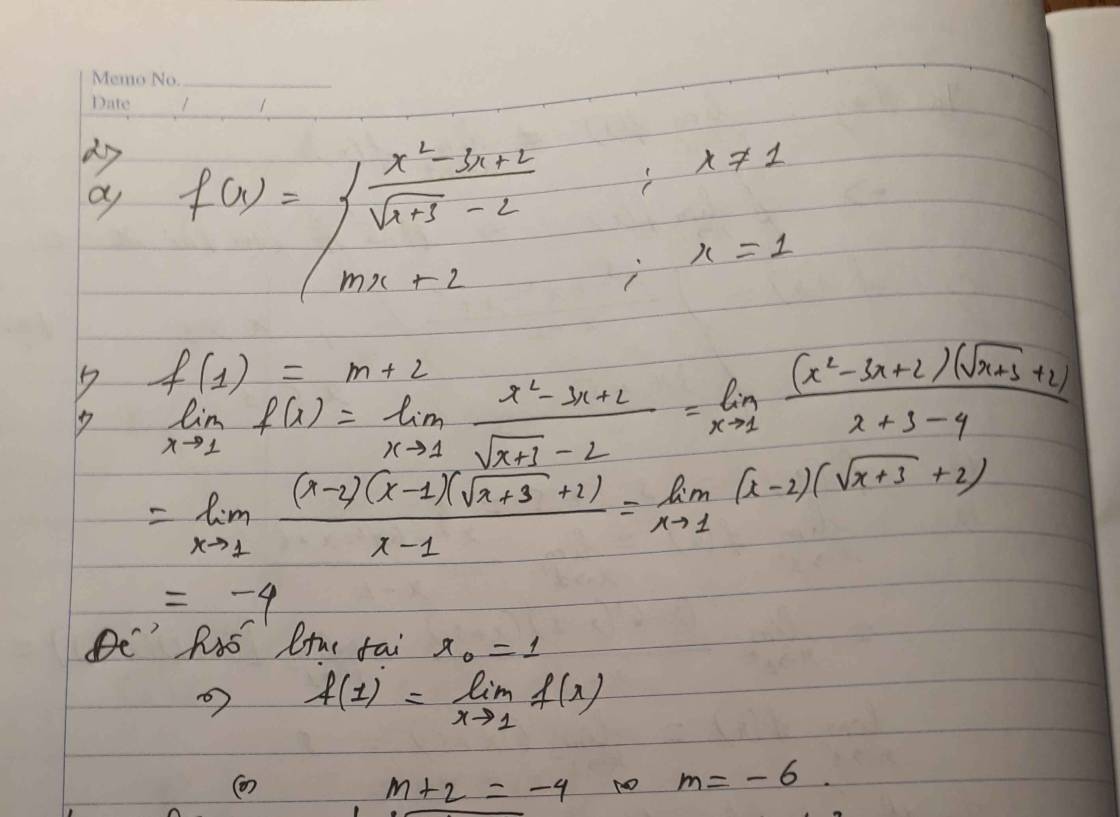Cho hàm số f(x) =\(\left\{{}\begin{matrix}-x^3;x\le-2\\\left|x\right|;-2< x< 2\\x^3-6;x\ge2\end{matrix}\right.\). f(x) là hàm số chẵn hay lẻ?

Những câu hỏi liên quan
cho hàm số \(\begin{matrix}\\\end{matrix}\)f(x) \(\left\{{}\begin{matrix}\sqrt{x+1}-2.khi,x\ge-1\\3x^2-x+1.khi,x< -1\end{matrix}\right.\)
giá trị f(-3) + f(0) bằng
Lời giải:
Do $-3<-1$ nên:
$f(-3)=3(-3)^2-(-3)+1=31$
Do $0> -1$ nên:
$f(0)=\sqrt{0+1}-2=-1$
$\Rightarrow f(-3)+f(0)=31+(-1)=30$
Đúng 0
Bình luận (0)
Cho hàm số fleft(xright)left{{}begin{matrix}2sin^2x+1,x 02^x;xge0end{matrix}right.. Giả sử Fleft(xright) là một nguyên hàm của hàm số fleft(xright) trên R và thỏa mãn điều kiện Fleft(1right)dfrac{2}{ln2}. Tính Fleft(-piright) A. Fleft(-piright)-2pi+dfrac{1}{ln2} B. Fleft(-piright)-2pi-dfrac{1}{ln2}C. Fleft(-piright)-pi-dfrac{1}{ln2} D. Fleft(-piright)-2piMình cần bài giải ạ, mình cảm ơn nhiều ♥
Đọc tiếp
Cho hàm số \(f\left(x\right)=\left\{{}\begin{matrix}2\sin^2x+1,x< 0\\2^x;x\ge0\end{matrix}\right.\). Giả sử \(F\left(x\right)\) là một nguyên hàm của hàm số \(f\left(x\right)\) trên \(R\) và thỏa mãn điều kiện \(F\left(1\right)=\dfrac{2}{ln2}\). Tính \(F\left(-\pi\right)\)
A. \(F\left(-\pi\right)=-2\pi+\dfrac{1}{ln2}\) B. \(F\left(-\pi\right)=-2\pi-\dfrac{1}{ln2}\)
C. \(F\left(-\pi\right)=-\pi-\dfrac{1}{ln2}\) D. \(F\left(-\pi\right)=-2\pi\)
Mình cần bài giải ạ, mình cảm ơn nhiều ♥
Xem thêm câu trả lời
Cho hàm số y=f(x)=\(\left\{{}\begin{matrix}2x^3-3\left(m+1\right)x^2+6mx-2\left(x< =3\right)\\nx+46\left(x>3\right)\end{matrix}\right.\)
trong đó m,n thuộc R. Tính tổng tất cả các giá trị nguyên của tham số m để hàm số y=f(x) có đúng ba điểm cực trị
- Với \(x< 3\Rightarrow f'\left(x\right)=6x^2-6\left(m+1\right)x+6m=6\left(x-1\right)\left(x-m\right)\)
\(f'\left(x\right)=0\Rightarrow6\left(x-1\right)\left(x-m\right)=0\left(1\right)\Rightarrow\left[{}\begin{matrix}x=1\\x=m\end{matrix}\right.\) có tối đa 2 cực trị khi \(x< 3\)
- Với \(x>3\Rightarrow f'\left(x\right)=n\) là hằng số \(\Rightarrow f\left(x\right)\) ko có cực trị khi \(x>3\)
\(\Rightarrow\) Hàm có đúng 3 điểm cực trị khi và chỉ khi nó đồng thời thỏa mãn:
ĐK1: \(f'\left(x\right)=0\) có 2 nghiệm pb khi \(x< 3\Rightarrow\left\{{}\begin{matrix}m< 3\\m\ne1\end{matrix}\right.\)
ĐK2: \(x=3\) là 1 cực trị của hàm số
\(\Rightarrow f\left(x\right)\) liên tục tại \(x=3\) đồng thời đạo hàm đổi dấu khi đi qua \(x=3\)
\(\lim\limits_{x\rightarrow3^+}f\left(x\right)=\lim\limits_{x\rightarrow3^-}f\left(x\right)\Leftrightarrow3n+46=25-9m\Rightarrow n=-3m-7\) (2)
Mặt khác do 2 nghiệm của (1) đều nhỏ hơn 3 \(\Rightarrow\) tại lân cận trái của \(x=3\) đạo hàm luôn có dấu dương
\(\Rightarrow\) Để đạo hàm đổi dấu khi đi qua \(x=3\) thì \(f'\left(3^+\right)=n< 0\)
Thế vào (2) \(\Rightarrow-3m-7< 0\Rightarrow m>-\dfrac{7}{3}\)
\(\Rightarrow-\dfrac{7}{3}< m< 3\Rightarrow\sum m=0\)
Đúng 0
Bình luận (0)
cho hàm số f(x) = \(\left\{{}\begin{matrix}\sqrt{x-1},x\ge2\\\dfrac{1}{x-3},x< 2\end{matrix}\right.\) chọn phát biểu sai:
a. f(2)=1
b. f(0)=\(\dfrac{-1}{3}\)
c. f(1)=0
d. f(10)=3
1/ Xét tính liên tục của hàm số tại một điểm:a) fleft(xright)left{{}begin{matrix}dfrac{x^2-4}{x^2+x-2};xne22x+1;x2end{matrix}right. tại x_02b) fleft(xright)left{{}begin{matrix}left(x+3right)^3-27;x0x^3+27;xle0end{matrix}right. tại x_00c) fleft(xright)left{{}begin{matrix}dfrac{x^3-6x^2-x+6}{x-1};x13x+5;xle1end{matrix}right. tại x_01d) fleft(xright)left{{}begin{matrix}dfrac{sqrt{3x+10}-x-4}{x+2};xne-2-dfrac{1}{4};x-2end{matrix}right. tại x_0-22/ Tìm m để hàm số sau liên tục tại điểm đã chỉ ra:a) ...
Đọc tiếp
1/ Xét tính liên tục của hàm số tại một điểm:
a) \(f\left(x\right)=\left\{{}\begin{matrix}\dfrac{x^2-4}{x^2+x-2};x\ne2\\2x+1;x=2\end{matrix}\right.\) tại \(x_0=2\)
b) \(f\left(x\right)=\left\{{}\begin{matrix}\left(x+3\right)^3-27;x>0\\x^3+27;x\le0\end{matrix}\right.\) tại \(x_0=0\)
c) \(f\left(x\right)=\left\{{}\begin{matrix}\dfrac{x^3-6x^2-x+6}{x-1};x>1\\3x+5;x\le1\end{matrix}\right.\) tại \(x_0=1\)
d) \(f\left(x\right)=\left\{{}\begin{matrix}\dfrac{\sqrt{3x+10}-x-4}{x+2};x\ne-2\\-\dfrac{1}{4};x=-2\end{matrix}\right.\) tại \(x_0=-2\)
2/ Tìm \(m\) để hàm số sau liên tục tại điểm đã chỉ ra:
a) \(f\left(x\right)=\left\{{}\begin{matrix}\dfrac{x^2-3x+2}{\sqrt{x+3}-2};x\ne1\\mx+2;x=1\end{matrix}\right.\) tại \(x_0=1\)
b) \(f\left(x\right)=\left\{{}\begin{matrix}\dfrac{\sqrt[3]{2x^2=9}-3}{2x-6};x\ne3\\m;x=3\end{matrix}\right.\) tại \(x_0=3\)
cho hàm số f(x)=\(\left\{{}\begin{matrix}x^2\\-x^3+bx+c\end{matrix}\right.\)\(\dfrac{khix\le0}{khix>0}\) có đạo hàm tại điểm x0=0 tính tổng c+2b
Hàm có đạo hàm tại \(x=0\) khi nó liên tục tại \(x=0\) và có đạo hàm trái bằng đạo hàm phải tại 0
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^+}\left(-x^3+bx+c\right)=c\)
\(\lim\limits_{x\rightarrow0^-}f\left(x\right)=\lim\limits_{x\rightarrow0^-}x^2=0\)
\(\Rightarrow c=0\)
\(f'\left(0^-\right)=2x_{x\rightarrow0^-}=0\)
\(f'\left(0^+\right)=\left(-3x^2+b\right)_{x\rightarrow0^+}=b\)
\(\Rightarrow b=0\Rightarrow b=c=0\)
Đúng 1
Bình luận (0)
cho hàm số y =f(x) =\(\left\{{}\begin{matrix}\dfrac{2}{x-1}\\\sqrt{x+1}\\x^{2^{ }}-1\end{matrix}\right.\)
khi x< 0 ; khi 0 ≤ x ≤ 2 ; khi x>2
a. Tìm tập xác định của hàm số.
b. Tính f(-1), f(0), f(1), f(2), f(3).
a: TXĐ: D=R
b: \(f\left(-1\right)=\dfrac{2}{-1-1}=\dfrac{2}{-2}=-1\)
\(f\left(0\right)=\sqrt{0+1}=1\)
\(f\left(1\right)=\sqrt{1+1}=\sqrt{2}\)
\(f\left(2\right)=\sqrt{3}\)
Đúng 1
Bình luận (0)
m.n ơi cứu mkgiúp mk bài này vs mk ko bt trình bày bài giải s cảCho hàm số f(x)left{{}begin{matrix}dfrac{2sqrt{x+2}-3}{x-1}x^2-1end{matrix}right. khi left{{}begin{matrix}xge2x 2end{matrix}right. Tính Pf(2) + f(-2) bằng bao nhiêu?A. Pdfrac{8}{3} B. P4 C. P6 D.Pdfrac{5}{3} m.n giúp mk vs chọn đáp án r giải chi tiết ra giúp mk đc ko? tại mk cần nhất là lời giải chi tiết ak để mk hiểu thêmmong m.n giúp mkhiện tại mk cần lời...
Đọc tiếp
m.n ơi cứu mk![]() giúp mk bài này vs mk ko bt trình bày bài giải s cả
giúp mk bài này vs mk ko bt trình bày bài giải s cả
Cho hàm số f(x)=\(\left\{{}\begin{matrix}\dfrac{2\sqrt{x+2}-3}{x-1}\\x^2-1\end{matrix}\right.\) khi \(\left\{{}\begin{matrix}x\ge2\\x< 2\end{matrix}\right.\) Tính P=f(2) + f(-2) bằng bao nhiêu?
A. P=\(\dfrac{8}{3}\) B. P=4 C. P=6 D.P=\(\dfrac{5}{3}\) m.n giúp mk vs chọn đáp án r giải chi tiết ra giúp mk đc ko? tại mk cần nhất là lời giải chi tiết ak để mk hiểu thêm![]() mong m.n giúp mk
mong m.n giúp mk
hiện tại mk cần lời giải rất gấp ak CẢM ƠN M.N RẤT NHIỀU![]()
Do \(2\in[2;+\infty)\Rightarrow\) khi \(x=2\) thì \(f\left(x\right)=\dfrac{2\sqrt{x+2}-3}{x-1}\Rightarrow f\left(2\right)=\dfrac{2\sqrt{2+2}-3}{2-1}=1\)
\(-2\in\left(-\infty;2\right)\) \(\Rightarrow\) khi \(x=-2\) thì \(f\left(x\right)=x^2-1\Rightarrow f\left(-2\right)=\left(-2\right)^2-1=3\)
\(\Rightarrow P=1+3=4\)
Đúng 0
Bình luận (1)
xét tính liên tục của hàm số
\(f\left(x\right)=\left\{{}\begin{matrix}\dfrac{9-x^2}{3-x}\\6\end{matrix}\right.\) khi x \(\ne3\), x = 3 tại x = 3
Lời giải:
\(\lim\limits_{x\to 3}f(x)=\lim\limits_{x\to 3}\frac{9-x^2}{3-x}=\frac{(3-x)(3+x)}{3-x}=\lim\limits_{x\to 3}(3+x)=3+3=6=f(3)\)
Do đó hàm số liên tục tại $x=3$.
Đúng 1
Bình luận (0)
\(\lim\limits_{x\rightarrow3}f\left(x\right)=\lim\limits_{x\rightarrow3}\dfrac{9-x^2}{3-x}=\lim\limits_{x\rightarrow3}3+x=3+3=6\)
\(f\left(3\right)=6\)
=>\(\lim\limits_{x\rightarrow3}f\left(x\right)=f\left(3\right)\)
=>Hàm số liên tục tại x=3
Đúng 0
Bình luận (0)
Bài 1: Xét tính chẵn lẻ của hàm số :y|x3-x|Bài 2: ho hàm số y f(x)left{{}begin{matrix}x-3,xge12x^2-x-3,x 1end{matrix}right. có đồ thị (C)a) Tính f(4),f(-1)b) Điểm nào sau đấy thuộc (c): A(4:1), b(-1,-4)Bài 3: Cho tập hợp A left{nin◻cdotleft|right|9⋮right} B (0;10)a)Liệt kê các phần tử của Ab) Tính Acap B, Acup B(mình đag cần rất gấp)
Đọc tiếp
Bài 1: Xét tính chẵn lẻ của hàm số :y=|x3-x|
Bài 2: ho hàm số y= f(x)=\(\left\{{}\begin{matrix}x-3,x\ge1\\2x^2-x-3,x< 1\end{matrix}\right.\) có đồ thị (C)
a) Tính f(4),f(-1)
b) Điểm nào sau đấy thuộc (c): A(4:1), b(-1,-4)
Bài 3: Cho tập hợp A= \(\left\{n\in◻\cdot\left|\right|9⋮\right\}\) B = (0;10)
a)Liệt kê các phần tử của A
b) Tính \(A\cap B\), \(A\cup B\)
(mình đag cần rất gấp)
Bài 1:
\(f\left(-x\right)=\left|\left(-x\right)^3+x\right|=\left|-x^3+x\right|=\left|-\left(x^3-x\right)\right|=\left|x^3-x\right|=f\left(x\right)\)
Vậy hàm số chẵn
Bài 2:
\(f\left(4\right)=4-3=1\\ f\left(-1\right)=2.1+1-3=0\\ b,\text{Thay }x=4;y=1\Leftrightarrow4-3=1\left(\text{đúng}\right)\\ \Leftrightarrow A\left(4;1\right)\in\left(C\right)\\ \text{Thay }x=-1;y=-4\Leftrightarrow2\left(-1\right)^2+1-3=-4\left(\text{vô lí}\right)\\ \Leftrightarrow B\left(-1;-4\right)\notin\left(C\right)\)
Đúng 0
Bình luận (0)