xét chiều biến thiên của các hàm số sau
\(y=x^3-2x^2+x+1\)
xét chiều biến thiên của các hàm số sau
\(y=x^3-2x^2+x+1\)
ta tính \(y'=3x^2-4x+1\)
\(y'=0\Rightarrow3x^2-4x+1=0\Rightarrow x=1;x=\frac{1}{3}\)
ta có
ta có trong khoảng 2 nghiệm thì y' cùng dấu với hệ số a, ngoài khoảng 2 nghiệm trái dấu với hệ số a
suy ra f'(x)>0 với \(x\in\left(-\infty;\frac{1}{3}\right)\cup\left(1;+\infty\right)\) suy ra hàm số đồng biến trên \(\left(-\infty;\frac{1}{3}\right)\cup\left(1;+\infty\right)\)
lại có f'(x)<0 với \(x\in\left(\frac{1}{3};1\right)\) suy ra hàm số nghịch biến trên \(\left(\frac{1}{3};1\right)\)
tìm m để hàm số sau đồng biến trên R
\(y=x^3-3x^2-mx-1\)
ta tính \(y'=3x^2-6x-m\)
để hàm số đồng biến trên R thì y'>0 với mọi x thuộc R
mà ta có \(y'=3x^2-6x-m\)>0 khi và chỉ khi \(\Delta=b^2-4ac
tìm m để hàm số sau nghịch biến trên R
\(y=-mx^3-3x^2+\left(2-m\right)x+3\)
ta tính \(y'=-3mx^2-6x+2-m\)
để hàm số nghịch biến trên R thì \(\)y'<0 với mọi x thuộc R ta có
y'<0 với mọi x thuộc R thì \(\begin{cases}-m
tìm cực trị của hàm số y=x-sin2x+2
TXĐ: R
y' = 1 - 2cos2x
y' = 0 ⇔x = kπ (k ∈ Z)
y'' = 2sin2x
x = kπ → y'' = 2 > 0
→ yCT = 1 tại x = kπ
Mình thường làm cách đơn giản hơn như sau:
1) y = x – sin2x + 2
Vì hàm sin 2x tuần hoàn trên đoạn [-Pi , Pi]
Nên ta chỉ cần xét y trên đoạn [ -Pi , Pi]
Y ‘ = 1 – 2cos2x => y’ = 0 <> x = +or-Pi/6 + k2Pi = +or- Pi/6 thuộc [ - Pi, Pi ]
Lập bảng biến thiên như bình thường hoặc tính y” như bạn hngth cũng được
Thường thì người ta bò họ no k2Pi đi chỉ xét trên chu kì cua nó thôi. Cái này bạn có thể mở SGK 11( NC) chương LG sẽ thấy
2)
Y = 3 – 2cosx + 1 – 2cos^2x = -2cos^2x – 2cosx + 4
Đặt: t = cosx , t thuộc [-1, 1]
Y = f(t) = -2t^2 – 2t +4 , D= [-1, 1]
Xét hàm f(t) như bình thường => hàm f(t) đạt CĐ tại t = -1/2 , fCĐ = f(-1/2) = 9/2
=>hàm y đạt CĐ tại x = +or-2P/3 + k2Pi và yCĐ = 9/2
Bài này mà giải theo cách trên giữ nguyên họ no thì giải tới sáng cũng chưa ra. Đây là 2 cách đơn giản nhất để tìm cực trị hs LG còn công thức thì ko có đâu
Xét các khoảng đơn điệu và tìm cực trị của hàm số
y = x + \(\sqrt{8-x^2}\)
Tập xác định: D=\(\left[-2\sqrt{2};2\sqrt{2}\right]\).
\(y'=1-\dfrac{x}{\sqrt{8-x^2}}\) = 0 \(\Rightarrow\) x=2.
Bảng biến thiên:
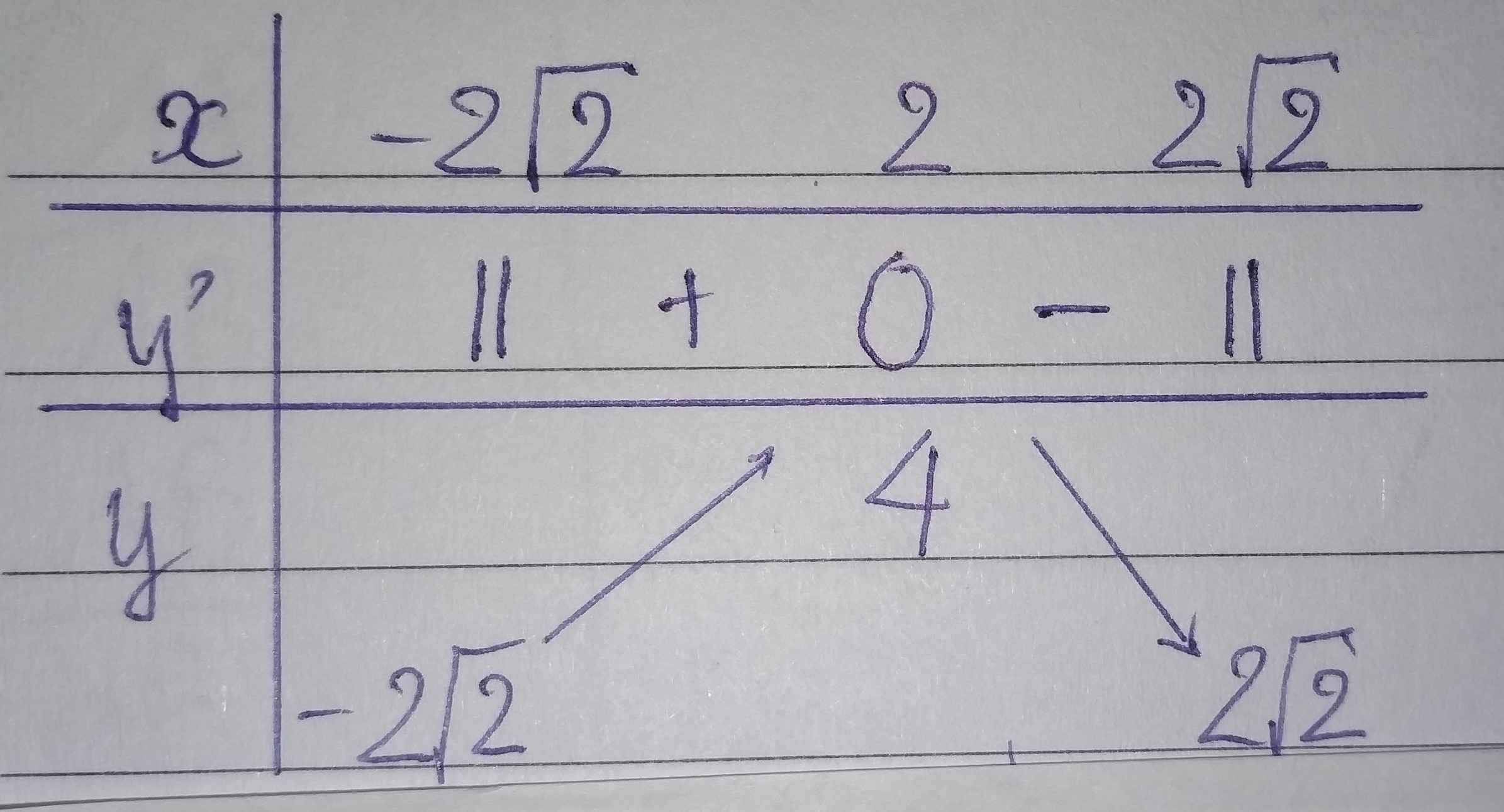
Vậy hàm số đã cho đồng biến trên khoảng (\(-2\sqrt{2}\);2), nghịch biến trên khoảng (2;\(2\sqrt{2}\)) và yCĐ=4 (tại x=2).
Tham khảo: Đồ thị:
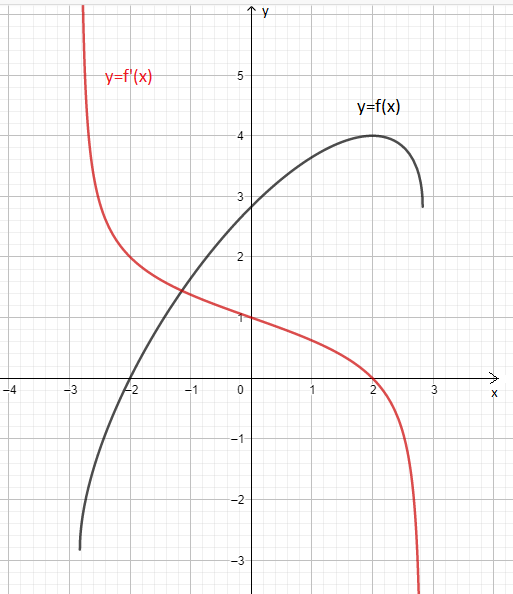
Tìm m để hàm số đạt cực trị y=x3-(m+2)x2+(1-m)x+3m-1 tại x1x2 thỏa l x1-x2 l =2
y'=3x2-2(m+2)x+1-m.
\(\Delta\)'=(m+2)2-3(1-m)=m2+7m+1>0 (để hàm số có hai điểm cực trị x1, x2).
|x1-x2|=2 \(\Leftrightarrow\) (x1+x2)2-4x1x2=4 \(\Leftrightarrow\) \(\left[\dfrac{2\left(m+2\right)}{3}\right]^2-4\dfrac{1-m}{3}=4\) \(\Rightarrow\) m=-8 (nhận) hoặc m=1 (nhận).
Xác định m để hệ phương trình có hai cặp nghiệm phân biệt
\(\begin{cases}\log_{\sqrt{3}}\left(x+1\right)-\log_{\sqrt{3}}\left(x-1\right)>\log_34\left(1\right)\\\log_2\left(x^2-2x+5\right)-m\log_{x^2-2x+5}2=5\left(2\right)\end{cases}\)
Điều kiện x>1
Từ (1) ta có \(\log_{\sqrt{3}}\frac{x+1}{x-1}>\log_34\) \(\Leftrightarrow\frac{x+1}{x-1}>2\) \(\Leftrightarrow\) 1<x<3
Đặt \(t=\log_2\left(x^2-2x+5\right)\)
Tìm điều kiện của t :
- Xét hàm số \(f\left(x\right)=\log_2\left(x^2-2x+5\right)\) với mọi x thuộc (1;3)
- Đạo hàm : \(f\left(x\right)=\frac{2x-2}{\ln2\left(x^2-2x+5\right)}>\) mọi \(x\in\left(1,3\right)\)
Hàm số đồng biến nên ta có \(f\left(1\right)\) <\(f\left(x\right)\) <\(f\left(3\right)\) \(\Leftrightarrow\)2<2<3
- Ta có \(x^2-2x+5=2'\)
\(\Leftrightarrow\) \(\left(x-1\right)^2=2'-4\)
Suy ra ứng với mõi giá trị \(t\in\left(2,3\right)\) ta luôn có 1 giá trị \(x\in\left(1,3\right)\)
Lúc đó (2) suy ra : \(t-\frac{m}{t}=5\Leftrightarrow t^2-5t=m\)
Xét hàm số : \(f\left(t\right)=t^2-5t\) với mọi \(t\in\left(2,3\right)\)
- Đạo hàm : \(f'\left(t\right)=2t-5=0\Leftrightarrow t=\frac{5}{2}\)
- Bảng biến thiên :
| x | 2 \(\frac{5}{2}\) 3 |
| y' | + 0 - |
| y | -6 -6 -\(\frac{25}{4}\) |
Để hệ có 2 cặp nghiệm phân biệt \(\Leftrightarrow-6>-m>-\frac{25}{4}\)\(\Leftrightarrow\)\(\frac{25}{4}\) <m<6
Tìm m để hệ có nghiệm (x, y) thỏa mãn điều kiện \(x\ge4\)
\(\begin{cases}\sqrt{x}+\sqrt{y}=3\\\sqrt{x+5}+\sqrt{y+3}\le m\end{cases}\)
\(\begin{cases}\sqrt{x}+\sqrt{y}=3\left(1\right)\\\sqrt{x+5}+\sqrt{y+3}\le m\left(2\right)\end{cases}\)
Điều kiện \(\begin{cases}x\ge0\\y\ge0\end{cases}\)
Đặt \(t=\sqrt{x}\) lúc đó (1) có dạng \(\sqrt{y=3-1}\Leftrightarrow y=\left(t^2-6t+9\right)\)
Điều kiện của t : \(2\le t\)\(\le3\)
Khi đó (2) \(\Leftrightarrow\sqrt{t^2+5}+\sqrt{t^2-6t+12}\le m\)
Xét hàm số : \(f\left(t\right)=\sqrt{t^2+5}+\sqrt{t^2-6t+12}\)
- Miền xác định \(D=\left[2;3\right]\)
- Đạo hàm
\(f'\left(t\right)=\frac{t}{\sqrt{t^2+5}}+\frac{t-3}{\sqrt{t^2-6t+12}}\)
\(f'\left(t\right)=0\Leftrightarrow\frac{t}{\sqrt{t^2+5}}=\frac{3-t}{\sqrt{t^2-6t+12}}\)
\(\Leftrightarrow t\sqrt{t^2-6t+12}=\left(3-t\right)\sqrt{t^2+5}\)
\(\Leftrightarrow t^4-6t^3+12t^2=t^4-6t^3+14t^2-30t+45\)
\(\Leftrightarrow2t^2-30t+45=0\) vô nghiệm với \(x\in D\)
Mà \(f'\left(3\right)>0\Rightarrow f\left(t\right)\) đồng biến trên D do đó min \(f\left(2\right)=5\)
Để có nghiệm (x,y) thỏa mãn \(x\ge4\Leftrightarrow\) (2) có nghiệm thỏa mãn (1)
và \(x\ge4\Leftrightarrow f\left(t\right)\le m\) thỏa mãn với mọi \(2\le t\)\(\le3\)
\(\Leftrightarrow\) min \(f\left(t\right)\le m\Leftrightarrow m\ge5\)
Tìm m để hệ có hai nhiệm với tung độ trái dấu :
\(\begin{cases}x^2+2\left|xy\right|-5x+m=0\\x-y=\sin\left|x\right|-\sin\left|y\right|\end{cases}\)
\(\begin{cases}x^2+2\left|xy\right|-5x+m=0\left(1\right)\\x-y=\sin\left|x\right|-\sin\left|y\right|\left(2\right)\end{cases}\)
Biến đổi (2) về dạng : \(x-\sin\left|x\right|=y-\sin\left|y\right|\)
\(\Leftrightarrow f\left(x\right)=f\left(y\right)\) (*)
Xét hàm số \(f\left(t\right)=t-\sin\left|t\right|\)
- Miền xác định D=R
- Đạo hàm \(f'\left(t\right)=\begin{cases}1-\cot\left(t>0\right)\\1+\cot\left(t<0\right)\end{cases}\)
Suy ra \(f'\left(t\right)\ge0\) với mọi \(t\ne0\Leftrightarrow\) Hàm số đồng biến
Từ (*) \(\Leftrightarrow x=y\) Thay vào (1) ta có : \(3x^2-5x+m=0\) (**)
Để hệ có hai nghiệm với tung độ trái dấu \(\Leftrightarrow\) phương trình (**) có 2 nghiệm trái dấu \(\Leftrightarrow P<0\Leftrightarrow m<0\)
Tìm m để hệ có nghiệm \(\begin{cases}3^x-3^y=\left(y-x\right)\left(xy+m\right)\\x^2+y^2=m\end{cases}\)
\(\begin{cases}3^x-3^y=\left(y-x\right)\left(xy+m\right)\left(1\right)\\x^2+y^2=m\left(2\right)\end{cases}\)
Thay (2) vào (1) ta có : \(3^x-3^y=\left(y-x\right)\left(xy+x^2+y^2\right)\)
\(\Leftrightarrow3^x-3^y=y^3-x^3\)
\(\Leftrightarrow3^x+x^3=3^y+y^3\)
\(\Leftrightarrow f\left(x\right)=f\left(y\right)\)
Xét hàm số \(f\left(t\right)=3'+t^3\)
- Miền xác định D=R
- Đạo hàm \(f'\left(x\right)=\ln3.3'+3t^2>0\) . Hàm đồng biến
Do dó x=y. Thay vào phương trình (2) ta có :
\(x^2+x^2=m\Leftrightarrow2x^2=m\Leftrightarrow x^2=\frac{m}{2}\)
Vậy để hệ có nghiệm : \(m\ge0\)