\(\sqrt{2-f\left(x\right)}=f\left(x\right)\Leftrightarrow\left\{{}\begin{matrix}f\left(x\right)\ge0\\f^2\left(x\right)+f\left(x\right)-2=0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}f\left(x\right)=1\\f\left(x\right)=-2< 0\left(loại\right)\end{matrix}\right.\) 

\(\Rightarrow f\left(1\right)=f\left(2\right)=f\left(3\right)=1\)

\(\sqrt{2g\left(x\right)-1}+\sqrt[3]{3g\left(x\right)-2}=2.g\left(x\right)\)

\(VT=1.\sqrt{2g\left(x\right)-1}+1.1\sqrt[3]{3g\left(x\right)-2}\)

\(VT\le\dfrac{1}{2}\left(1+2g\left(x\right)-1\right)+\dfrac{1}{3}\left(1+1+3g\left(x\right)-2\right)\)

\(\Leftrightarrow VT\le2g\left(x\right)\)

Dấu "=" xảy ra khi và chỉ khi \(g\left(x\right)=1\)

\(\Rightarrow g\left(0\right)=g\left(3\right)=g\left(4\right)=g\left(5\right)=1\)

Để các căn thức xác định \(\Rightarrow\left\{{}\begin{matrix}f\left(x\right)-1\ge0\\g\left(x\right)-1\ge0\end{matrix}\right.\)

Ta có:

\(\sqrt{f\left(x\right)-1}+\sqrt{g\left(x\right)-1}+f\left(x\right).g\left(x\right)-f\left(x\right)-g\left(x\right)+1=0\)

\(\Leftrightarrow\sqrt{f\left(x\right)-1}+\sqrt{g\left(x\right)-1}+\left[f\left(x\right)-1\right]\left[g\left(x\right)-1\right]=0\)

\(\Leftrightarrow\left\{{}\begin{matrix}f\left(x\right)=1\\g\left(x\right)=1\end{matrix}\right.\) \(\Leftrightarrow x=3\)

Vậy tập nghiệm của pt đã cho có đúng 1 phần tử

1/ nhân 4 cả 2 vế lên, vế trái sẽ trở thành (2x+1)(2x+2)^2(2x+3), nhân 2x+1 với 2x+3, cái bình phương phân tích ra
thành (4x^2+8x+3)(4x^2+8x+4)=72
đặt 4x^2+8x+4=a \(\left(a\ge0\right)\)

thay vào ta có (a-1)a=72 rồi bạn phân tích thành nhân tử sẽ có nghiệm là 9 và -8 loại được -8 thì nghiệm của a là 9
suy ra 2x+1=3 hoặc -3, tính ra được x rồi nhân vào với nhau

2/\(\Leftrightarrow5\sqrt{\left(x+1\right)\left(x^2-x+1\right)}=2\left[\left(x+1\right)+\left(x^2-x+1\right)\right]\)

đặt căn x+1=a, căn x^2-x+1=b (a,b>=0)
thay vào ra là \(2a^2-5ab+2b^2=0\\ \Leftrightarrow\left(a-2b\right)\left(2a-b\right)=0\)

suy ra a=2b hoặc b=2a, thay cái kia vào bình phương lên giải nốt phương trình rồi nhân nghiệm với nhau

Nghiệm nguyên.

2x+3=(2x+1)+2

\(\left(1\right)\Leftrightarrow\left[\left(2x+1\right)\left(x+1\right)\right]^2+2\left(2x+1\right)\left(x+1\right)^2=18\\ \)

2x+1 luôn lẻ---> x+1 phải chẵn --> x phải lẻ---> x=2n-1

\(\left(4n+3\right)\left(2n\right)^2\left(4n+1\right)=18\)

18 không chia hết co 4 vậy vô nghiệm nguyên.

Viết diễn dải dài suy luận logic rất nhanh

câu 2.

\(2\left(x^2+2\right)>0\forall x\) thực tế  >=4  không cần vì mình cần so sánh với 0

\(\left(2\right)\Leftrightarrow25\left(x^3+1\right)=4\left(x^2+2\right)^2\)

Vậy đáp số là (16-25)/4=-9/4

1) Phương trình ban đầu tương đương :

\(\left(2021x-2020\right)^3=\left(2x-2\right)^3+\left(2019x-2018\right)^3\)

Đặt \(a=2x-2,b=2019x-2018\)

\(\Rightarrow a+b=2021x-2020\)

Khi đó phương trình có dạng :

\(\left(a+b\right)^3=a^3+b^3\)

\(\Leftrightarrow3ab\left(a+b\right)=0\)

\(\Leftrightarrow3\cdot\left(2x-2\right)\cdot\left(2019x-2018\right)\cdot\left(2021x-2002\right)=0\)

\(\Leftrightarrow\)Hoặc \(2x-2=0\) 

          Hoặc \(2019x-2018=0\)

          Hoặc \(2021x-2020=0\)

\(\Rightarrow x\in\left\{1,\frac{2018}{2019},\frac{2020}{2021}\right\}\) (thỏa mãn)

Vậy : phương trình đã cho có tập nghiệm \(S=\left\{1,\frac{2018}{2019},\frac{2020}{2021}\right\}\)

\(x\left(2x-3\right)+x\left(x-m\right)=3x^2+x-m\)

\(\Leftrightarrow2x^2-3x+x^2-xm=3x^2+x-m\)

\(\Leftrightarrow-3x-xm=x-m\)

\(\Leftrightarrow4x+xm=m\Leftrightarrow x\left(4+m\right)=m\)

\(\Leftrightarrow x=\frac{m}{m+4}\)

Phương trình có nghiệm không âm \(\Leftrightarrow x\ge0\)

\(\Rightarrow\frac{m}{m+4}\ge0\)

Mà \(m+4>m\)nên \(\orbr{\begin{cases}m\ge0\\m+4\le0\end{cases}}\Leftrightarrow\orbr{\begin{cases}m\ge0\\m\le-4\end{cases}}\)

\(\Leftrightarrow x^2-4x+5+3\sqrt{x^2-4x+5}-2=0\)

Đặt \(\sqrt{x^2-4x+5}=t>0\)

\(\Rightarrow t^2+3t-2=0\Rightarrow\left[{}\begin{matrix}t=\dfrac{-3+\sqrt{17}}{2}\\t=\dfrac{-3-\sqrt{17}}{2}\left(loại\right)\end{matrix}\right.\)

\(\Rightarrow x^2-4x+5=\dfrac{13-3\sqrt{17}}{2}\)

\(\Leftrightarrow x^2-4x+\dfrac{-3+3\sqrt{17}}{2}=0\)

\(x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2=4^2-2\left(\dfrac{-3+3\sqrt{17}}{2}\right)=19-3\sqrt{17}\)

Không hiểu câu hỏi lắm :vvv

`a,(x+3)(x^2+2021)=0`

`x^2+2021>=2021>0`

`=>x+3=0`

`=>x=-3`

`2,x(x-3)+3(x-3)=0`

`=>(x-3)(x+3)=0`

`=>x=+-3`

`b,x^2-9+(x+3)(3-2x)=0`

`=>(x-3)(x+3)+(x+3)(3-2x)=0`

`=>(x+3)(-x)=0`

`=>` $\left[ \begin{array}{l}x=0\\x=-3\end{array} \right.$

`d,3x^2+3x=0`

`=>3x(x+1)=0`

`=>` $\left[ \begin{array}{l}x=0\\x=-1\end{array} \right.$

`e,x^2-4x+4=4`

`=>x^2-4x=0`

`=>x(x-4)=0`

`=>` $\left[ \begin{array}{l}x=0\\x=4\end{array} \right.$

1) a) \(\left(x+3\right).\left(x^2+2021\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x+3=0\\x^2+2021=0\end{matrix}\right.\\\left[{}\begin{matrix}x=-3\left(nhận\right)\\x^2=-2021\left(loại\right)\end{matrix}\right. \)

=> S={-3}

Bài 1: 

a) Ta có: \(\left(x+3\right)\left(x^2+2021\right)=0\)

mà \(x^2+2021>0\forall x\)

nên x+3=0

hay x=-3

Vậy: S={-3}

Bài 2: 

b) Ta có: \(x\left(x-3\right)+3\left(x-3\right)=0\)

\(\Leftrightarrow\left(x-3\right)\left(x+3\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\x+3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-3\end{matrix}\right.\)

Vậy: S={3;-3}

Đặt \(f\left(x\right)=\dfrac{x-1}{\left(x-2\right)\left(x-3\right)}.\)

 \(x-1=0.\Leftrightarrow x=1.\\ x-2=0.\Leftrightarrow x=2.\\ x-3=0.\Leftrightarrow x=3.\)

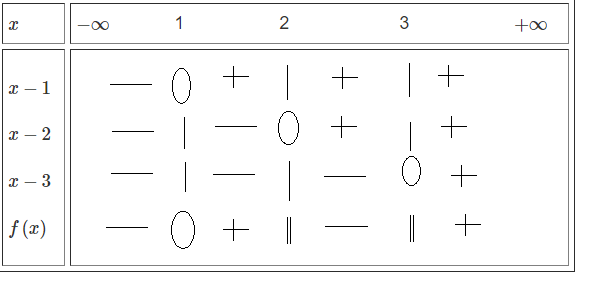
\(\Rightarrow f\left(x\right)>0\Leftrightarrow x\in\) \(\left(1;2\right)\cup\left(3;+\infty\right).\)

\(\Rightarrow B.\)

b