-Đặt \(\left\{{}\begin{matrix}b+c-a=x>0\\c+a-b=y>0\\a+b-c=z>0\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}2c=x+y\\2a=y+z\\2b=z+x\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}c=\dfrac{x+y}{2}\\a=\dfrac{y+z}{2}\\b=\dfrac{z+x}{2}\end{matrix}\right.\)

\(A=\dfrac{a}{b+c-a}+\dfrac{b}{c+a-b}+\dfrac{c}{a+b-c}=\dfrac{\dfrac{y+z}{2}}{x}+\dfrac{\dfrac{z+x}{2}}{y}+\dfrac{\dfrac{x+y}{2}}{z}=\dfrac{1}{2}\left(\dfrac{y+z}{x}+\dfrac{z+x}{y}+\dfrac{x+y}{z}\right)=\dfrac{1}{2}\left[\left(\dfrac{y}{x}+\dfrac{x}{y}\right)+\left(\dfrac{z}{y}+\dfrac{y}{z}\right)+\left(\dfrac{x}{z}+\dfrac{z}{x}\right)\right]\ge\dfrac{1}{2}.\left(2+2+2\right)=3\left(đpcm\right)\)

-Dấu "=" xảy ra khi \(a=b=c\)

 +  +  ≥ 3.

Đặt b + c – a = x > 0 (1); a + c – b = y > 0  (2); a + b – c = z > 0  (3)

Cộng (1) và (2) => b + c – a + a + c – b = x + y ⇔ 2c = x + y ⇔ c =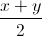 

Tương tự a = 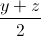 ; b =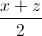 

Do đó  +  +  =  +   +  = ( +  +  +  +  + )

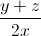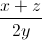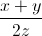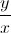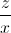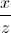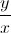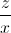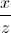= [( + ) + ( + ) + ( + )] ≥ (2 + 2 + 2) = 3.

Vậy  +  +  ≥ 3.

\(\Leftrightarrow ab\left(\dfrac{1}{b+c}-\dfrac{1}{a+c}\right)+bc\left(\dfrac{1}{a+c}-\dfrac{1}{a+b}\right)+ca\left(\dfrac{1}{a+b}-\dfrac{1}{b+c}\right)=0\)

\(\Leftrightarrow\dfrac{ab\left(a-b\right)}{\left(b+c\right)\left(a+c\right)}+\dfrac{bc\left(b-c\right)}{\left(a+b\right)\left(a+c\right)}+\dfrac{ca\left(c-a\right)}{\left(a+b\right)\left(b+c\right)}=0\)

\(\Leftrightarrow\dfrac{ab\left(a^2-b^2\right)+bc\left(b^2-c^2\right)+ca\left(c^2-a^2\right)}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}=0\)

\(\Leftrightarrow\dfrac{\left(a-b\right)\left(b-c\right)\left(a-c\right)\left(a+b+c\right)}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}=0\)

\(\Leftrightarrow\left[{}\begin{matrix}a=b\\b=c\\c=a\end{matrix}\right.\) hay tam giác cân

Lời giải:

Đặt \((b+c-a, c+a-b, a+b-c)=(x,y,z)\Rightarrow (a,b,c)=(\frac{y+z}{2}; \frac{x+z}{2}; \frac{x+y}{2})\)

Tất nhiên $x,y,z>0$ vì $a,b,c$ là 3 cạnh tam giác.

Khi đó, áp dụng BĐT Cô-si cho các số dương:

\(\frac{a}{b+c-a}+\frac{b}{a+c-b}+\frac{c}{a+b-c}=\frac{y+z}{2x}+\frac{x+z}{2y}+\frac{x+y}{2z}\)

\(\geq 3\sqrt[3]{\frac{(y+z)(x+z)(x+y)}{8xyz}}\geq 3\sqrt[3]{\frac{2\sqrt{yz}.2\sqrt{xz}.2\sqrt{xy}}{8xyz}}=3\)

Ta có đpcm

b) Vẫn cách đặt giống phần a. Áp dụng BĐT Cô-si:

\(\frac{a}{a+b-c}+\frac{b}{b+c-a}+\frac{c}{c+a-b}=\frac{y+z}{2z}+\frac{x+z}{2x}+\frac{x+y}{2y}=\frac{y}{2z}+\frac{z}{2x}+\frac{x}{2y}+\frac{3}{2}\)

\(\geq 3\sqrt[3]{\frac{y}{2z}.\frac{z}{2x}.\frac{x}{2y}}+\frac{3}{2}=\frac{3}{2}+\frac{3}{2}=3\)

Ta có đpcm.

Ta có:

\(AB^2=BC\cdot BH=c^2=a\cdot c'\)

\(\Rightarrow c\cdot c=a\cdot c'\Rightarrow\dfrac{a}{c}=\dfrac{c}{c'}\)

Vậy đáp án đúng là D