+ 
+ 
≥ 3.
Đặt b + c – a = x > 0 (1); a + c – b = y > 0 (2); a + b – c = z > 0 (3)
Cộng (1) và (2) => b + c – a + a + c – b = x + y ⇔ 2c = x + y ⇔ c =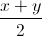 
Tương tự a =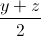 
; b =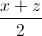 
Do đó + + = 
+ 
+ 
= 
(
+ 
+ 
+ 
+ 
+ 
)
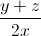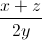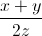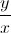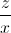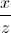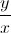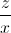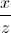= [( + ) + ( + ) + ( + )] ≥ (2 + 2 + 2) = 3.
Vậy + + ≥ 3.
Cho a, b, c là 3 cạnh của 1 tam giác. Chứng minh: \(1< \dfrac{a}{b+c}+\dfrac{b}{a+c}+\dfrac{c}{a+b}< 2\)
Cho a;b;c là 3 cạnh tam giác. Chứng minh:
\(\sqrt{\dfrac{a}{b+c-a}}+\sqrt{\dfrac{b}{c+a-b}}+\sqrt{\dfrac{c}{a+b-c}}\ge3\)
Cho tam giác ABC có độ dài 3 cạnh là a, b, c thỏa mãn: \(\dfrac{ab}{b+c}+\dfrac{bc}{c+a}+\dfrac{ac}{a+b}=\dfrac{ac}{b+c}+\dfrac{ab}{c+a}+\dfrac{bc}{a+b}\). Chứng minh: Tam giác ABC cân
Cho tam giác ABC có độ dài 3 cạnh là a, b, c thỏa mãn: \(\dfrac{ab}{b+c}+\dfrac{bc}{a+c}+\dfrac{ac}{a+b}=\dfrac{ac}{b+c}+\dfrac{ab}{a+c}+\dfrac{bc}{a+b}\). Chứng minh tam giác ABC cân
cho a,b,c là 3 cạnh của tam giác.Chứnh minh rằng:
\(A=\dfrac{a}{b+c-a}+\dfrac{b}{a+c-b}+\dfrac{c}{a+b-a}\ge3\)
Cho a, b, c là độ dài 3 cạnh và x, y, z là độ dài 3 đường phân giác trong tam giác của các góc đối diện với cạnh đó. Chứng minh: \(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}>\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\)
Cho a,b,c là 3 cạnh của một tam giác .Chứng minh rằng
A=\(\dfrac{a}{b+c-a}+\dfrac{b}{a+c-b}+\dfrac{c}{a+b-c}>3\)
Cho a,b,c là đôh dài 3 cạnh của 1 tam giác. Chứng minh :
\(P=\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}< 2\)
Cho a,b,c là độ dài 3 cạnh tam giác
Chứng minh \(\dfrac{1}{a+b},\dfrac{1}{c+a},\dfrac{1}{b+c}\) là độ dài 3 cạnh tam giác
