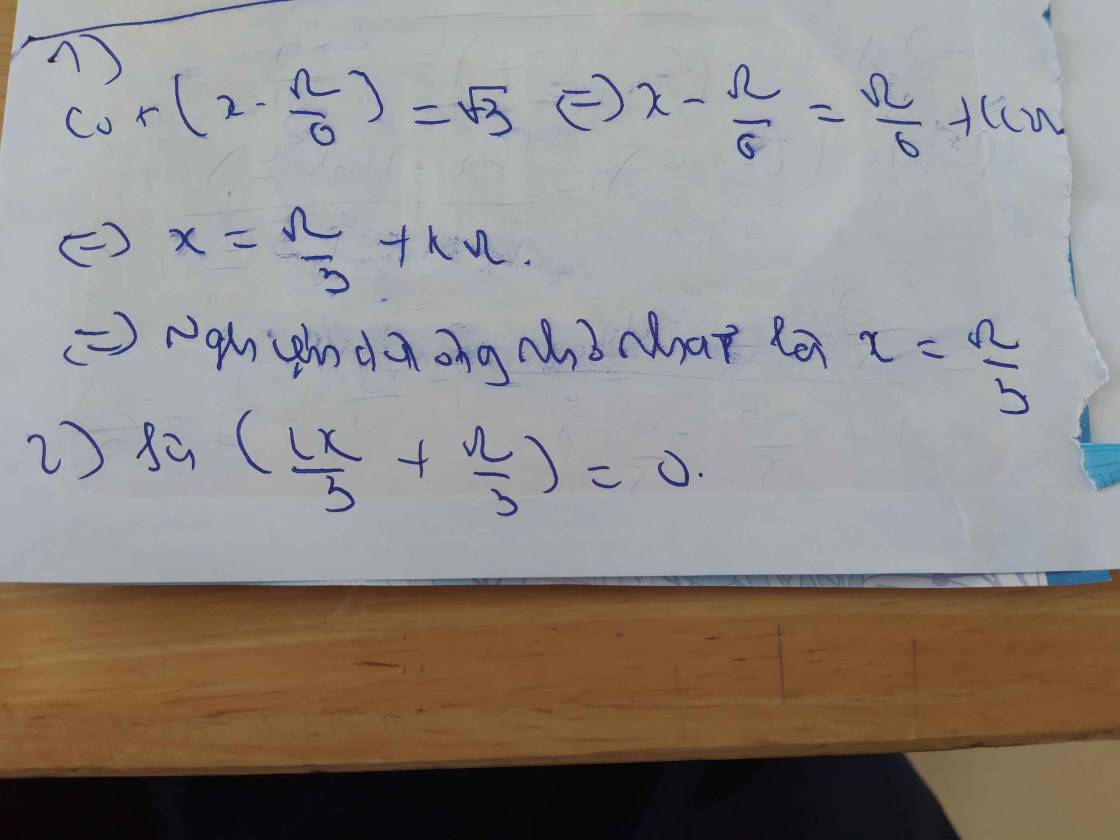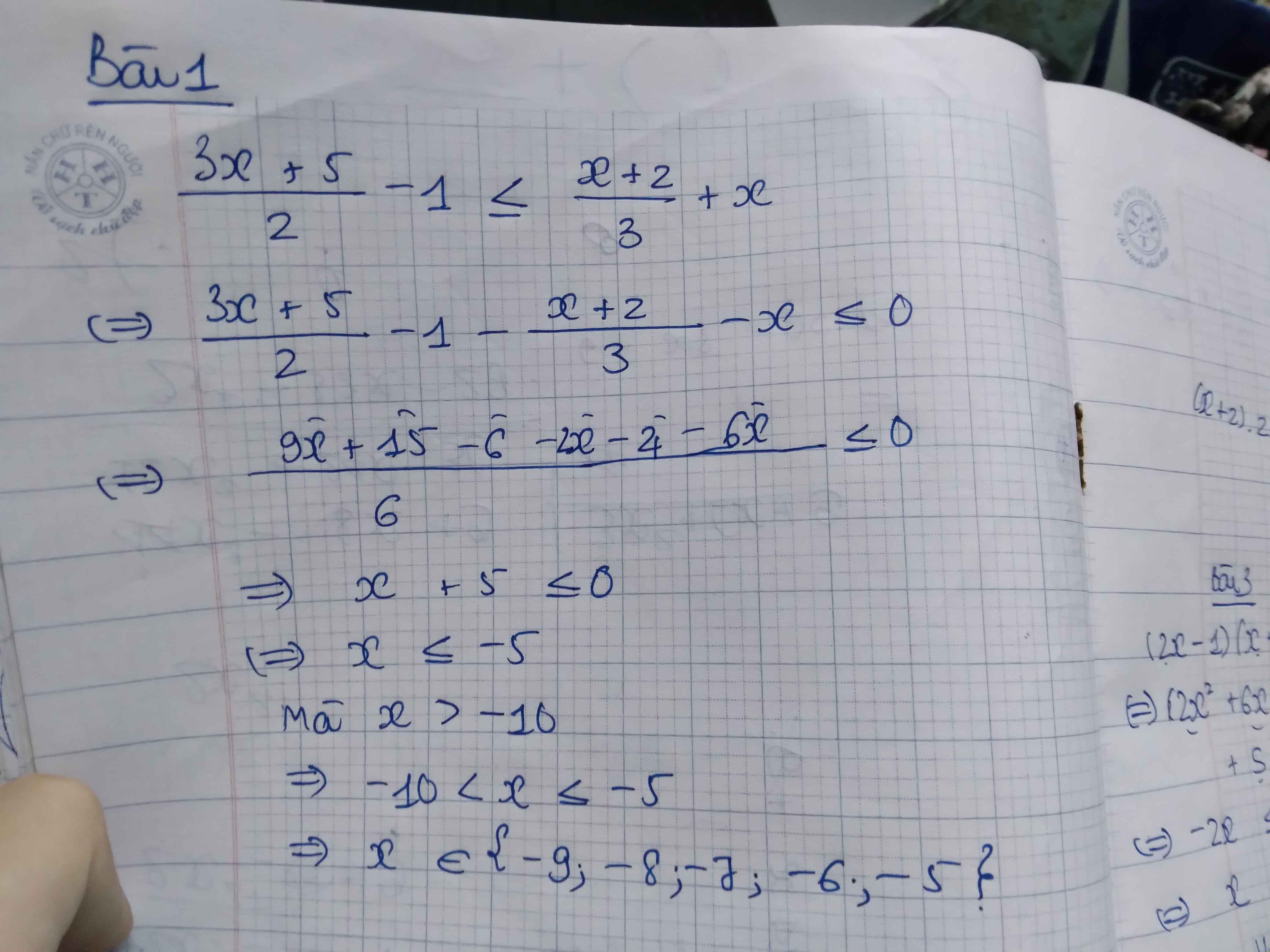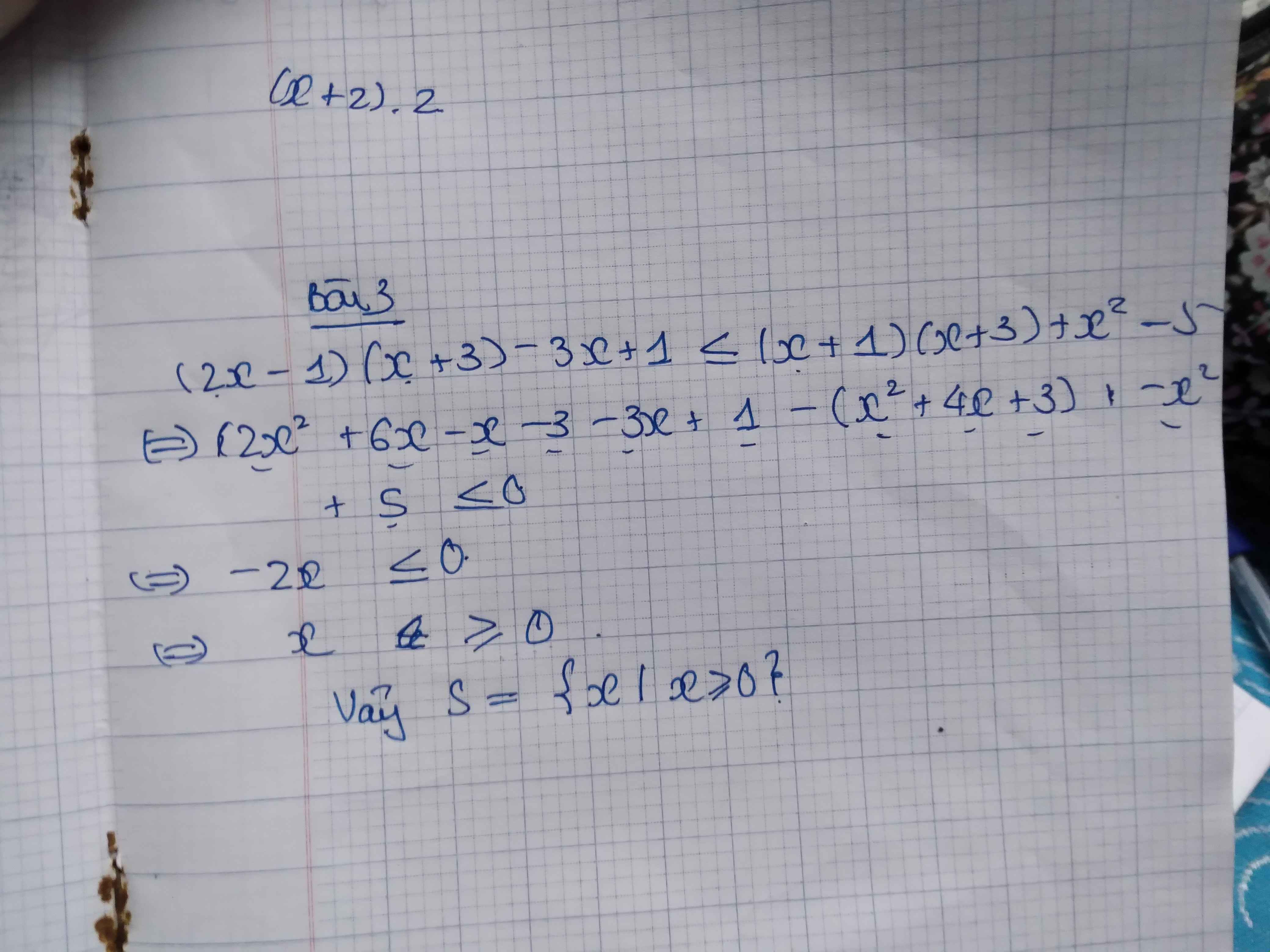1B

2B

3D

4D

\(\sqrt{3}cosx+2sin^2\left(\dfrac{x}{2}-\pi\right)=1\) 

\(\Leftrightarrow\sqrt{3}cosx+2sin^2\dfrac{x}{2}=1\)

\(\Leftrightarrow\sqrt{3}cosx-cosx=0\Leftrightarrow cosx=0\Leftrightarrow x=\dfrac{\pi}{2}+k\pi\) ( k thuộc Z )

Vậy ... 

22.

Nhận thấy \(cosx=0\) không phải nghiệm, chia 2 vế cho \(cos^2x\)

\(3tan^2x+2tanx-1=0\)

\(\Leftrightarrow\left[{}\begin{matrix}tanx=-1\\tanx=\dfrac{1}{3}\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{4}+k\pi\\x=arctan\left(\dfrac{1}{3}\right)+k\pi\end{matrix}\right.\)

Nghiệm dương nhỏ nhất của pt là: \(x=arctan\left(\dfrac{1}{3}\right)\)

22. PT đã cho tương đương

3 - 4cos²x + 2 sinxcosx = 0

⇔ 3 - 2 - 2cos2x + sin2x = 0

⇔ 1 - 2cos2x + sin2x = 0

⇔ 1 + sin2x = 2cos2x

⇔ sin\(\dfrac{\pi}{2}\) + sin2x = 2cos2x

⇔ \(2sin\left(\dfrac{\pi}{4}+x\right).cos\left(\dfrac{\pi}{4}-x\right)\) = 2cos2x

Do \(\left(\dfrac{\pi}{4}-x\right)+\left(\dfrac{\pi}{4}+x\right)=\dfrac{\pi}{2}\) 

⇒ \(sin\left(\dfrac{\pi}{4}+x\right)=cos\left(\dfrac{\pi}{4}-x\right)\)

Vậy sin²\(\left(x+\dfrac{\pi}{4}\right)\) = cos2x

Cái này là hiển nhiên ????

a) \(x-\sqrt{2x+3}=-2x\)

\(\Leftrightarrow\sqrt{2x+3}=x+2x\)

\(\Leftrightarrow\sqrt{2x+3}=3x\)

\(\Leftrightarrow2x+3=9x^2\)

\(\Leftrightarrow9x^2-2x-3=0\)

\(\Rightarrow\Delta=\left(-2\right)^2-4\cdot9\cdot\left(-3\right)=112>0\)

\(\Leftrightarrow\left[{}\begin{matrix}x_1=\dfrac{2+\sqrt{112}}{18}=\dfrac{1+2\sqrt{7}}{9}\\x_2=\dfrac{2-\sqrt{112}}{18}=\dfrac{1-2\sqrt{7}}{9}\end{matrix}\right.\)

b) \(\dfrac{1}{x}=1-\dfrac{1}{x+1}\) (ĐK: \(x\ne0,x\ne-1\))

\(\Leftrightarrow\dfrac{1}{x}+\dfrac{1}{x+1}=1\)

\(\Leftrightarrow\dfrac{x+1}{x\left(x+1\right)}+\dfrac{x}{x\left(x+1\right)}=1\)

\(\Leftrightarrow\dfrac{x+1+x}{x\left(x+1\right)}=1\)

\(\Leftrightarrow\dfrac{2x+1}{x^2+x}=1\)

\(\Leftrightarrow2x+1=x^2+1\)

\(\Leftrightarrow x^2-2x=0\)

\(\Leftrightarrow x\left(x-2\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(ktm\right)\\x-2=0\end{matrix}\right.\)

\(\Leftrightarrow x=2\left(tm\right)\)

c) \(\dfrac{2}{\sqrt{x+3}}=\dfrac{1}{\sqrt{x^2-9}}\) (ĐK: \(x\ge3\))

\(\Leftrightarrow2\sqrt{x^2-2}=\sqrt{x+3}\)

\(\Leftrightarrow\sqrt{4\left(x^2-9\right)}=\sqrt{x+3}\)

\(\Leftrightarrow4\left(x^2-9\right)=x+3\)

\(\Leftrightarrow4x^2-36=x+3\)

\(\Leftrightarrow4x^2-x-36-3=0\)

\(\Leftrightarrow4x^2-x-39=0\)

\(\Rightarrow\Delta=\left(-1\right)^2-4\cdot4\cdot\left(-39\right)=625>0\)

\(\Leftrightarrow\left[{}\begin{matrix}x_1=\dfrac{1+\sqrt{625}}{8}=\dfrac{13}{4}\left(tm\right)\\x_2=\dfrac{1-\sqrt{625}}{8}=-3\left(ktm\right)\end{matrix}\right.\)

Bài 1 :

Ta có : \(\dfrac{3x+5}{2}-1\le\dfrac{x+2}{3}+x\)

\(\Leftrightarrow\dfrac{3x+5}{2}-1-\dfrac{x+2}{3}-x\le0\)

\(\Leftrightarrow\dfrac{3\left(3x+5\right)-6-2\left(x+2\right)-6x}{6}\le0\)

\(\Leftrightarrow9x+15-6-2x-4-6x\le0\)

\(\Leftrightarrow x\le-5\)

Mà \(\left\{{}\begin{matrix}x\in Z\\x>-10\end{matrix}\right.\)

Vậy \(x\in\left\{-5;-6;-7;-8;-9\right\}\)

b3\(\Leftrightarrow2x^2+5x-3-3x+1\le x^2+2x-3+x^2-5\\ \Leftrightarrow0.x\le-6\Leftrightarrow x\in\varnothing\)

TXĐ: \(x>-4\)

Khi đó BPT tương đương:

\(x^2+2x>3\Leftrightarrow x^2+2x-3>0\)

\(\Rightarrow\left[{}\begin{matrix}x>1\\x< -3\end{matrix}\right.\)

Vậy tập nghiệm của BPT là: \(\left[{}\begin{matrix}x>1\\-3< x< -3\end{matrix}\right.\)

\(B=\dfrac{\sqrt{2}-1}{\left(\sqrt{2}-1\right)\left(\sqrt{2}+1\right)}+\dfrac{\sqrt{3}-\sqrt{2}}{\left(\sqrt{3}-\sqrt{2}\right)\left(\sqrt{3}+\sqrt{2}\right)}+...+\dfrac{\sqrt{100}-\sqrt{99}}{\left(\sqrt{100}-\sqrt{99}\right)\left(\sqrt{100}+\sqrt{99}\right)}\)

\(=\dfrac{\sqrt{2}-1}{1}+\dfrac{\sqrt{3}-\sqrt{2}}{1}+...+\dfrac{\sqrt{100}-\sqrt{99}}{1}\)

\(=\sqrt{100}-1=9\)

\(x^3+3.9x^2+3.9^2x+9^3=0\)

\(\Leftrightarrow\left(x+9\right)^3=0\)

\(\Leftrightarrow x=-9\)

Bài 2. 

ĐK: $x\geq \frac{-11}{2}$

$x+\sqrt{2x+11}=0\Leftrightarrow x=-\sqrt{2x+11}$

\(\Rightarrow \left\{\begin{matrix} x\leq 0\\ x^2=2x+11\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\leq 0\\ x^2-2x-11=0(*)\end{matrix}\right.\)

\(\Delta'(*)=12\)

\(\Rightarrow x=1\pm \sqrt{12}=1\pm 2\sqrt{3}\). Với điều kiện của $x$ suy ra $x=1-2\sqrt{3}$

$\Rightarrow a=1; b=-2\Rightarrow ab=-2$

Bài 1. 

Đặt $x^2+2x=t$ thì PT ban đầu trở thành:

$t^2-t-m=0(1)$

Để PT ban đầu có 4 nghiệm phân biệt thì:

Trước tiên PT(1) cần có 2 nghiệm phân biệt. Điều này xảy ra khi $\Delta (1)=1+4m>0\Leftrightarrow m> \frac{-1}{4}(*)$

Với mỗi nghiệm $t$ tìm được, thì PT $x^2+2x-t=0(2)$ cần có 2 nghiệm $x$ phân biệt. 

Điều này xảy ra khi $\Delta '(2)=1+t>0\Leftrightarrow t>-1$

Vậy ta cần tìm điều kiện của $m$ để (1) có hai nghiệm $t$ phân biệt đều lớn hơn $-1$

Điều này xảy ra khi \(\left\{\begin{matrix} (t_1+1)(t_2+1)>0\\ t_1+t_2+2>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} t_1t_2+t_1+t_2+1>0\\ t_1+t_2+2>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} -m+1+1>0\\ 1+2>0\end{matrix}\right.\Leftrightarrow m< 2(**)\)

Từ $(*); (**)\Rightarrow \frac{-1}{4}< m< 2$

b) 

Để pt ban đầu vô nghiệm thì PT(1) vô nghiệm hoặc có 2 nghiệm $t$ đều nhỏ hơn $-1$

PT(1) vô nghiệm khi mà $\Delta (1)=4m+1<0\Leftrightarrow m< \frac{-1}{4}$

Nếu PT(1) có nghiệm thì $t_1+t_2=1>-2$ nên 2 nghiệm $t$ không thể cùng nhỏ hơn $-1$

Vậy PT ban đầu vô nghiệm thì $m< \frac{-1}{4}$

c) Để PT ban đầu có nghiệm duy nhất thì:

\(\left\{\begin{matrix} \Delta (1)=1+4m=0\\ \Delta' (2)=1+t=0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} m=-\frac{1}{4}\\ t=-1\end{matrix}\right.\).Mà với $m=-\frac{1}{4}$ thì $t=\frac{1}{2}$ nên hệ trên vô lý. Tức là không tồn tại $m$ để PT ban đầu có nghiệm duy nhất. 

d) 

Ngược lại phần b, $m\geq \frac{-1}{4}$

e) 

Để PT ban đầu có nghiệm kép thì PT $(2)$ có nghiệm kép. Điều này xảy ra khi $\Delta' (2)=1+t=0\Leftrightarrow t=-1$

$t=-1\Leftrightarrow m=(-1)^2-(-1)=2$

a. Áp dụng công thức L'Hospital:

\(\lim\limits_{x\to 0}\frac{\sqrt{x+1}-\sqrt{1-x}}{\sqrt[3]{x+1}-\sqrt{1-x}}=\lim\limits_{x\to 0}\frac{\frac{1}{2}(x+1)^{\frac{-1}{2}}+\frac{1}{2}(1-x)^{\frac{-1}{2}}}{\frac{1}{3}(x+1)^{\frac{-2}{3}}+\frac{1}{2}(1-x)^{\frac{-1}{2}}}=\frac{1}{\frac{5}{6}}=\frac{6}{5}\)

b.

\(\lim\limits_{x\to 0}(\frac{1}{x}-\frac{1}{x^2})=\lim\limits_{x\to 0}\frac{x-1}{x^2}=-\infty\)

c. Áp dụng quy tắc L'Hospital:

\(\lim\limits_{x\to +\infty}\frac{x^4-x^3+11}{2x-7}=\lim\limits_{x\to +\infty}\frac{4x^3-3x^2}{2}=+\infty \)

d.

\(\lim\limits_{x\to 5}\frac{7}{(x-1)^2}.\frac{2x+1}{2x-3}=\frac{7}{(5-1)^2}.\frac{2.5+11}{2.5-3}=\frac{11}{16}\)