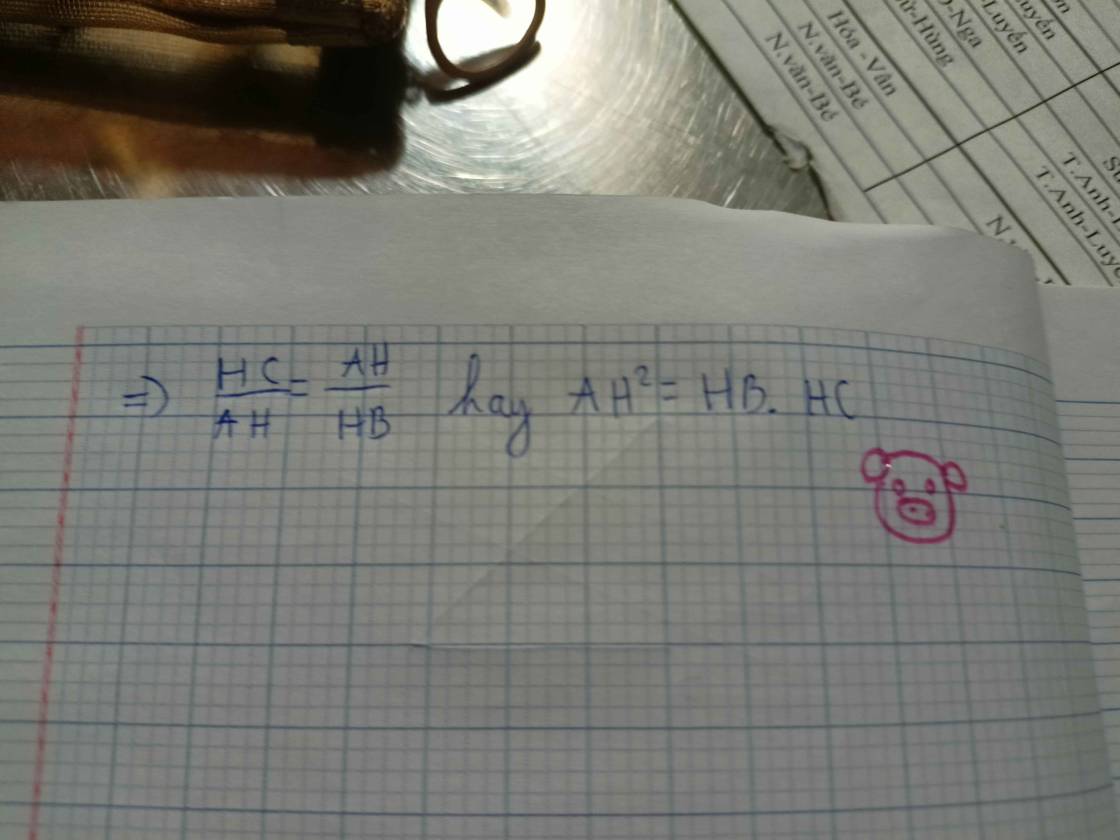Cho \(\Delta\)ABC vuông tại A , đường cao AH ;tia phân giác của góc B cắt AH tại I và AC tại D . CM: HI.CD=AD.AI

Những câu hỏi liên quan
Cho \(\Delta ABC\) vuông tại \(A\), \(AH\) là đường cao
\(a\)) Chứng minh \(\Delta HBA\) đồng dạng \(\Delta ABC\)
\(b\)) Chứng minh \(\Delta AH^2=BH.HC\)
a)xét ΔABC và ΔHBA ta có
\(\widehat{BAH}=\widehat{BHA}=90^o\)
\(\widehat{B}chung\)
=>ΔABC ∼ ΔHBA(g.g)(1)
b)xét ΔABC và ΔAHC ta có
\(\widehat{BAC}=\widehat{AHC}=90^o\)
\(\widehat{B}chung\)
->ΔABC ∼ ΔAHC(g.g)(2)
từ (1) và (2)=>ΔHBA và ΔAHC
->\(\dfrac{AH}{BH}=\dfrac{HC}{AH}\)
=>\(AH^2=BH.HC\)
Đúng 2
Bình luận (2)
Cho Delta ABC vuông tại A left(AB ACright) có đường cao AH a) Chứng minh Delta HBAsim Delta ABCb) Trên đoạn thẳng AH lấy điểm D. Qua C vẽ đường thẳng vuông góc với BD cắt tia AH tại E. Chứng minh widehat{HBD}widehat{HEC} và BH.CHHD.HEc) Chứng minh dfrac{EH}{AH}dfrac{EA}{AD}
Đọc tiếp
Cho \(\Delta ABC\) vuông tại \(A\) \(\left(AB< AC\right)\) có đường cao \(AH\)
\(a\)) Chứng minh \(\Delta HBA\sim\) \(\Delta ABC\)
\(b\)) Trên đoạn thẳng \(AH\) lấy điểm \(D\). Qua \(C\) vẽ đường thẳng vuông góc với \(BD\) cắt tia \(AH\) tại \(E\). Chứng minh \(\widehat{HBD}=\widehat{HEC}\) và \(BH.CH=HD.HE\)
\(c\)) Chứng minh \(\dfrac{EH}{AH}=\dfrac{EA}{AD}\)
a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
=>ΔHBA đồng dạng với ΔABC
Đúng 0
Bình luận (0)
Câu 1: Cho tam giác ABC vuông tại A, có đường cao AH.a) Chứng minh Delta ABC tỉ lệ với Delta HACb)Chứng minh AC^2BC.CHCâu 2: Cho tam giác ABC vuông tại A, có đường cao AH. Biết HB4cm,HC9cm.a) Chứng minh: AH^2HB.HCb) Tính diện tích tam giác ABCCâu 3: Cho hình chữ nhật ABCD có AB8cm, BC6cm. Vẽ đường cao AH của Delta ADB a) Tính DBb) Chứng minh Delta ADH~Delta ADBc) Chứng minh AD^2DH.DBd) Chứng minh Delta AHB~Delta BCD Giúp mik vs ạ
Đọc tiếp
Câu 1: Cho tam giác ABC vuông tại A, có đường cao AH.
a) Chứng minh \(\Delta ABC\) tỉ lệ với \(\Delta HAC\)
b)Chứng minh \(AC^2\)=BC.CH
Câu 2: Cho tam giác ABC vuông tại A, có đường cao AH. Biết HB=4cm,HC=9cm.
a) Chứng minh: \(AH^2\)=HB.HC
b) Tính diện tích tam giác ABC
Câu 3: Cho hình chữ nhật ABCD có AB=8cm, BC=6cm. Vẽ đường cao AH của \(\Delta ADB\)
a) Tính DB
b) Chứng minh \(\Delta ADH~\Delta ADB\)
c) Chứng minh \(AD^2\)=DH.DB
d) Chứng minh \(\Delta AHB~\Delta BCD\)
Giúp mik vs ạ
2:
a: Xét ΔHAB vuông tại H và ΔHCA vuông tại H có
góc HAB=góc HCA
=>ΔHAB đồng dạng với ΔHCA
=>HA/HC=HB/HA
=>HA^2=HB*HC
b: BC=4+9=13cm
AH=căn 4*9=6cm
S ABC=1/2*6*13=39cm2
Đúng 0
Bình luận (0)
1/ Cho \(\Delta ABC\)vuông tại A, đường cao AH=42cm. Biết AB:AC = 3:7. Tính BH,CH?
2/ Cho \(\Delta ABC\)vuông tại A, đường cao AH=48cm. Biết BH:CH = 9:16. Tính AB, AC
1 / xét tam giác ABH đồng dạng vs CAH trg hợp g-g suy ra AB/AC =BH/AH
<=> 3 /7 =BH /42
=> BH =18 cm
2 áp dụng hệ thức lượng AH^2 =BH .CH từ bh/ch =9/16 =>CH= 16BH/9
TA CÓ AH ^2 =16BH^2 /9 SUY RA BH =36 cm SUY RA CH = 64 cm áp dụng pita go suy ra AB ,AC hoặc hệ thức lg cũng đc
Đúng 0
Bình luận (0)
Bài 2: Cho \(\Delta\)ABC vuông tại A, có AB = 4 cm, BC = 5 cm. Tính đường cao AH
\(Pytago:\)
\(AC^2=BC^2-AB^2\)
\(\Rightarrow AC=\sqrt{BC^2-AB^2}=\sqrt{5^2-4^2}=3\left(cm\right)\)
Áp dung HTL trong tam giác vuông ABC có :
\(AB\cdot AC=AH\cdot BC\\ \Leftrightarrow AH=\dfrac{AB\cdot AC}{BC}=\dfrac{3\cdot4}{5}=2.4\left(cm\right)\)
Đúng 3
Bình luận (0)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow AC^2=BC^2-AB^2=5^2-4^2=9\)
hay \(AC=\sqrt{9}=3cm\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AB\cdot AC=BC\cdot AH\)
\(\Leftrightarrow AH\cdot5=3\cdot4=12\)
hay AH=2,4cm
Vậy: AH=2,4cm
Đúng 0
Bình luận (0)
Cho DeltaABC vuông tại A,kẻ đường cao AH1)Chứng minh:DeltaABC đồng dạng DeltaHAC2)Cho AB6cm,AC8cm.Tính BC,AH3)Từ H kẻ HEperpAC.Chứng minh:^{HE^2}EA.EC4)Gọi I là trung điểm của AH,EI cắt AB tại F.Chứng minh:^{AH^2}FA.FB+EA.EC
Đọc tiếp
Cho \(\Delta\)ABC vuông tại A,kẻ đường cao AH
1)Chứng minh:\(\Delta\)ABC đồng dạng \(\Delta\)HAC
2)Cho AB=6cm,AC=8cm.Tính BC,AH
3)Từ H kẻ HE\(\perp\)AC.Chứng minh:\(^{HE^2}\)=EA.EC
4)Gọi I là trung điểm của AH,EI cắt AB tại F.Chứng minh:\(^{AH^2}\)=FA.FB+EA.EC
a/ Xét \(\Delta ABC\) và \(\Delta HAC\) có :
\(\left\{{}\begin{matrix}\widehat{C}chung\\\widehat{BAC}=\widehat{AHC}=90^0\end{matrix}\right.\)
\(\Leftrightarrow\Delta ABC\sim HAC\left(g-g\right)\)
b/ \(BC=\sqrt{AB^2+AC^2}=10cm\)
\(AH.BC=AB.AC\Leftrightarrow AH=\dfrac{AB.AC}{BC}=4,8cm\)
c/ \(\Delta HEA\sim\Delta CEH\left(g-g\right)\)
\(\Leftrightarrow\dfrac{HE}{CE}=\dfrac{EA}{HE}\Leftrightarrow HE^2=EA.EC\left(đpcm\right)\)
Đúng 2
Bình luận (0)

a) Xét ΔHAC và ΔABC có:
∠(ACH ) là góc chung
∠(BAC)= ∠(AHC) = 90o
⇒ ΔHAC ∼ ΔABC (g.g)
b) Xét ΔHAD và ΔBAH có:
∠(DAH ) là góc chung
∠(ADH) = ∠(AHB) = 90o
⇒ ΔHAD ∼ ΔBAH (g.g)

c) Tứ giác ADHE có 3 góc vuông ⇒ ADHE là hình chữ nhật.
⇒ ΔADH= ΔAEH ( c.c.c) ⇒ ∠(DHA)= ∠(DEA)
Mặt khác: ΔHAD ∼ ΔBAH ⇒ ∠(DHA)= ∠(BAH)
∠(DEA)= ∠(BAH)
Xét ΔEAD và ΔBAC có:
∠(DEA)= ∠(BAH)
∠(DAE ) là góc chung
ΔEAD ∼ ΔBAC (g.g)

d) ΔEAD ∼ ΔBAC

ΔABC vuông tại A, theo định lí Pytago:

Theo b, ta có:
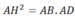


Đúng 1
Bình luận (0)
1) Xét ΔABC vuông tại A và ΔHAC vuông tại H có
\(\widehat{C}\) chung
Do đó: ΔABC\(\sim\)ΔHAC(g-g)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho \(\Delta ABC\) vuông tại A, đường cao AH, đường trung tuyến AO, đường phân giác AD. Đường thẳng vuông góc với AO tại A và vuông góc với BC tại B cắt nhau ở P, PC cắt AH ở E.
a) C/m \(OP\perp AB\)
b) C/m E là trung điểm của AH
\(a,\) Vì AO là trung tuyến ứng ch BC của tg ABC nên \(AO=OB\)
Hay tg AOB cân tại O
\(\Rightarrow\widehat{OAB}=\widehat{OBA}\Rightarrow90^0-\widehat{OAB}=90^0-\widehat{OBA}\)
\(\Rightarrow\widehat{PAB}=\widehat{PBA}\) hay tg PAB cân tại P
\(\Rightarrow AP=PB\) hay P thuộc trung trực của AB
Mà \(AO=OB\) nên O thuộc trung trực AB
Do đó OP là đg trung trực của AB
Vậy \(OP\perp AB\)
Đúng 1
Bình luận (0)
\(\Delta ABC\) vuông tại A. Đường cao AH = 24cm. AB:AC = 3:4. BH, CH = ?
Ta có: \(\dfrac{AB}{AC}=\dfrac{3}{4}\)
\(\Leftrightarrow\dfrac{HB}{HC}=\dfrac{9}{16}\)
\(\Leftrightarrow HB=\dfrac{9}{16}\cdot HC\)
Ta có: \(AH^2=HB\cdot HC\)
\(\Leftrightarrow HC^2\cdot\dfrac{9}{16}=24^2\)
\(\Leftrightarrow HC=32\left(cm\right)\)
hay HB=18(cm)
Đúng 2
Bình luận (0)
Cho \(\Delta ABC\) vuông tại A, đường cao AH, Gọi D, E theo thứ tự là hình chiếu trên AB và AC
a) CM: \(\Delta ABC\sim\Delta HBA\)
b) Cho \(HB=4cm;HC=9cm\) Tính \(AB,DE\)
c) CM: \(AD.AB=AE.AC\)
`a)` Xét `\triangle ABC` vuông tại `A` có: `\hat{B}+\hat{C}=90^o`
Xét `\triangle ABH` vuông tại `H` có: `\hat{B}+\hat{A_1}=90^o`
`=>\hat{C}=\hat{A_1}`
Xét `\triangle ABC` và `\triangle HBA` có:
`{:(\hat{C}=\hat{A_1}),(\hat{B}\text{ là góc chung}):}}=>\triangle ABC` $\backsim$ `\triangle HBA` (g-g)
`b)` Ta có: `BC=HB+HC=4+9=13(cm)`
Xét `\triangle ABC` vuông tại `A` có: `AH` là đường cao
`@AH=\sqrt{BH.HC}=6 (cm)`
`@AB=\sqrt{BH.BC}=2\sqrt{13}(cm)`
Ta có: `\hat{DEA}=\hat{ADH}=\hat{AEH}=90^o`
`=>` Tứ giác `AEHD` là hcn `=>DE=AH=6(cm)`
`c)` Xét `\triangle AHB` vuông tại `H` có: `HD \bot AB=>AH^2=AD.AB`
Xét `\triangle AHC` vuông tại `H` có: `HE \bot AC=>AH^2=AE.AC`
`=>AD.AB=AE.AC`

Đúng 3
Bình luận (3)
4. Cho \(\Delta\)ABC vuông tại A , đường cao AH. Biết AC=4cm, BC=5cm
a. Tính AB,AH,HB,HC
b. Tính diện tích, chu vi của tam giác ABC và đường trung tuyến AM
c. Kẻ đường cao MI của tam giác AMC. Tính Mi
a: AB=căn 5^2-4^2=3cm
Xét ΔABC vuông tại A có AH là đường cao
nên AB^2=BH*BC; AC^2=CH*BC; AH*BC=AB*AC
=>AH=3*4/5=2,4cm; BH=3^2/5=1,8cm
CH=5-1,8=3,2cm
b: C=3+4+5=12cm
S=1/2*3*4=6cm2
AM=BC/2=2,5cm
c: MA=MC=2,5cm
AC=4cm
ΔMAC cân tại M có MI là đường cao
nên I là trung điểm của AC
=>IA=IC=AC/2=2cm
MI=căn MA^2-IA^2=1,5cm
Đúng 0
Bình luận (0)