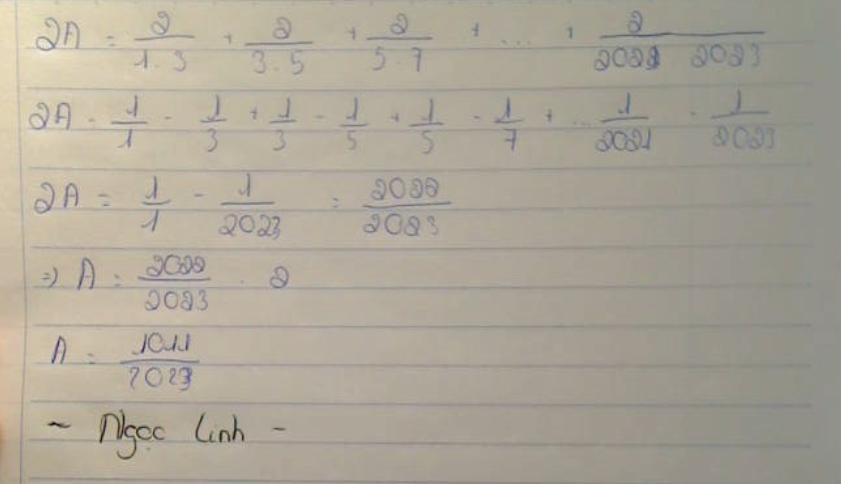\(B=\dfrac{1}{1.3}+\dfrac{1}{3.5}+\dfrac{1}{5.7}+...+\dfrac{1}{97.99}\)

\(B=\dfrac{1}{1}\cdot\dfrac{1}{3}+\dfrac{1}{3}\cdot\dfrac{1}{5}+\dfrac{1}{5}\cdot\dfrac{1}{7}+...+\dfrac{1}{97}\cdot\dfrac{1}{99}\)

\(B=\dfrac{1}{1}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{97}-\dfrac{1}{99}\)

\(B=\dfrac{1}{1}-\dfrac{1}{99}\)

\(B=\dfrac{99}{99}-\dfrac{1}{99}\)

\(B=\dfrac{98}{99}\)

#YVA

B=\(\dfrac{1}{1.3}+\dfrac{1}{3.5}+\dfrac{1}{5.7}+...+\dfrac{1}{97.99}\)

B=\(\left(\dfrac{2}{1.3}+\dfrac{2}{3.5}+\dfrac{2}{5.7}+...+\dfrac{2}{97.99}\right):2\)

B=\(\left(\dfrac{1}{1}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+\dfrac{1}{97}-\dfrac{1}{99}\right):2\)

B=\(\left(\dfrac{1}{1}-\dfrac{1}{99}\right):2\)

B=\(\dfrac{98}{99}:2\)

B=\(\dfrac{49}{99}\)

\(A=\dfrac{1}{3.5}+\dfrac{1}{5.7}+...+\dfrac{1}{97.99}\)

⇔ \(2A=2\left(\dfrac{1}{3.5}+\dfrac{1}{5.7}+...+\dfrac{1}{97.99}\right)\)

⇔ 2A = \(\dfrac{2}{3.5}+\dfrac{2}{5.7}+...+\dfrac{2}{97.99}\)

⇔ 2A = \(\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{97}-\dfrac{1}{99}\)

⇔ 2A = \(\dfrac{1}{3}-\dfrac{1}{99}\)

⇔ 2A = \(\dfrac{32}{99}\)

⇔ A = \(\dfrac{32}{99}:2\)

⇔ A = \(\dfrac{16}{99}\)

\(A=\dfrac{1}{3.5}+\dfrac{1}{5.7}+......+\dfrac{1}{97.99}\)

\(\Leftrightarrow2A=\dfrac{2}{3.5}+\dfrac{2}{5.7}+......+\dfrac{2}{97.99}\)

\(\Leftrightarrow2A=\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+.....+\dfrac{1}{97}-\dfrac{1}{99}\)

\(\Leftrightarrow2A=\dfrac{1}{3}-\dfrac{1}{99}\)

\(\Leftrightarrow2A=\dfrac{32}{99}\)

\(\Leftrightarrow A=\dfrac{16}{99}\)

A=\(\dfrac{1}{3.5}+\dfrac{1}{5.7}+...+\dfrac{1}{97.99}\)

2A=\(\dfrac{2}{3.5}+\dfrac{2}{5.7}+...+\dfrac{2}{97.99}\)

2A=\(\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{9}\)+...\(+\dfrac{1}{97}-\dfrac{1}{99}\)

2A=\(\dfrac{1}{3}-\dfrac{1}{99}\)

2A=\(\dfrac{32}{99}\)

A=\(\dfrac{32}{99}:2\)

A=\(\dfrac{16}{99}\)

Chúc bạn học tốt

\(\dfrac{2}{3\cdot5}+\dfrac{2}{5\cdot7}+...+\dfrac{2}{95\cdot97}+\dfrac{2}{97\cdot99}\)

\(=\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{95}-\dfrac{1}{97}+\dfrac{1}{97}-\dfrac{1}{99}\)

\(=\dfrac{1}{3}-\dfrac{1}{99}\)

\(=\dfrac{33}{99}-\dfrac{1}{99}\)

\(=\dfrac{32}{99}\)

\(\dfrac{2}{3.5}+\dfrac{2}{5.7}+...+\dfrac{2}{95.97}+\dfrac{2}{97.99}\)

\(\Rightarrow\dfrac{2}{3}-\dfrac{2}{5}+\dfrac{2}{5}-\dfrac{2}{7}+...+\dfrac{2}{95}-\dfrac{2}{97}+\dfrac{2}{97}-\dfrac{2}{99}\)

\(\Rightarrow\dfrac{2}{3}-\dfrac{2}{99}=\dfrac{64}{99}\)

chúc bạn học tốt

\(M=\dfrac{2}{3.5}+\dfrac{2}{5.7}+\dfrac{2}{7.9}+...+\dfrac{2}{97.99}\)

\(M=2.(\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{97}-\dfrac{1}{99})\)

\(M=2.\left(\dfrac{1}{3}-\dfrac{1}{99}\right)\)

\(M=2.\dfrac{32}{99}\)

\(M=\dfrac{64}{99}\)

http://vietjack.com/giai-sach-bai-tap-toan-6/bai-95-trang-28-sach-bai-tap-toan-6-tap-2.jsp

\(m=\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{9}+...+\dfrac{1}{97}-\dfrac{1}{99}=\dfrac{1}{3}-\dfrac{1}{99}=\dfrac{32}{99}\)

\(B=\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+\dfrac{2}{5\cdot7}+...+\dfrac{2}{97\cdot99}+\dfrac{2}{99\cdot101}\\ B=\dfrac{1}{1}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{97}-\dfrac{1}{99}+\dfrac{1}{99}-\dfrac{1}{101}\\ B=\dfrac{1}{1}-\dfrac{1}{101}\\ B=\dfrac{101}{101}-\dfrac{1}{101}\\ B=\dfrac{100}{101}\)

a, đặt đề bài là A

Ta có : A=( 1-1/2+1/2-1/3+...+1/9-1/10).(x-1)+1/10.x=x-9/10

= (1-1/10).(x-1)+1/10.x

= 9/10 .( x-1 )+1/10.x

=1.x-9/10

nên x= 0 hoặc 1

với -1 nữa nha

chữ xấu (thông cảm) ;-;

\(A=1.\dfrac{1}{3}+\dfrac{1}{3}.\dfrac{1}{5}+...+\dfrac{1}{2021}.\dfrac{1}{2023}=1-\dfrac{1}{2023}=\dfrac{2022}{2023}\)

\(A=\dfrac{1}{2}\left(\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+...+\dfrac{2}{2021\cdot2023}\right)\)

\(=\dfrac{1}{2}\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{2021}-\dfrac{1}{2023}\right)\)

\(=\dfrac{1}{2}\cdot\dfrac{2022}{2023}=\dfrac{1011}{2023}\)

\(=2\cdot\left(\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{9}+...+\dfrac{1}{97}-\dfrac{1}{99}+\dfrac{1}{99}-\dfrac{1}{101}\right)\)

\(=2\cdot\left(\dfrac{1}{3}-\dfrac{1}{101}\right)=2\cdot\dfrac{98}{303}=\dfrac{196}{303}\)

= 2/3 . 2/5 + 2/5 . 2/7 + ... + 2/99 . 2/101

= 2/3 - 2/5 + 2/5 - 2/7 + ... + 2/99 - 2/101

= 2/3 - 2/101

= 196/303

2/3 - 2/5 + 2/5 - 2/7 + 2/7 - 2/9 + .... + 2/97 - 2/99 + 2/99 - 2/101

 = 2/3 - 2/101

= 196/303