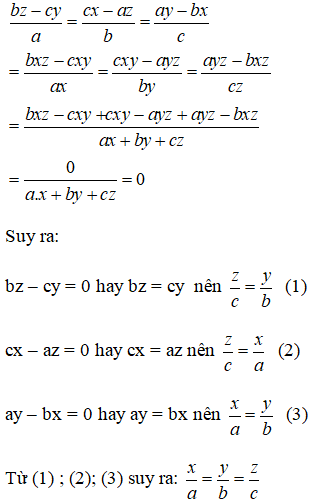Nếu \(\dfrac{bz-cy}{a}=\dfrac{cx-az}{b}=\dfrac{ay-bx}{c}\)thì x;y;z tương ứng tỉ lệ với a;b;c

Những câu hỏi liên quan
\(\dfrac{bz-cy}{z}=\dfrac{cx-az}{b}=\dfrac{ay-bx}{c}\) (1) CMR: \(\dfrac{x}{a}=\dfrac{y}{b}=\dfrac{z}{c}\) (*)
Lời giải:
Sửa đề: $z$ đầu tiên ở mẫu đổi thành $a$.
Ta có:
$\frac{bz-cy}{a}=\frac{cx-az}{b}=\frac{ay-bx}{c}$
$=\frac{abz-cya}{a^2}=\frac{bcx-abz}{b^2}=\frac{acy-bcx}{c^2}$
$=\frac{abz-cya+bcx-abz+acy-bcx}{a^2+b^2+c^2}=\frac{0}{a^2+b^2+c^2}=0$
$\Rightarrow bz-cy=cx-az=ay-bx=0$
$\Rightarrow bz=cy; cx=az; ay=bx$
$\Rightarrow \frac{x}{a}=\frac{y}{b}=\frac{z}{c}$
Ta có đpcm.
Đúng 2
Bình luận (0)
cho \(\dfrac{cy-bz}{x}=\dfrac{az-cx}{y}=\dfrac{bx-ay}{z}\) chứng minh rằng :\(\dfrac{a}{x}=\dfrac{b}{y}=\dfrac{c}{z}\)
Ta có :
\(\dfrac{cy-bx}{x}=\dfrac{az-cx}{y}=\dfrac{bx-ay}{z}=\dfrac{bxz-cxy+cxy-ayz+ayz-bxz}{ax+by+cz}=0\)
\(\Rightarrow\dfrac{cy-bz}{x}=0\) \(\Rightarrow cy=bz\) \(\Rightarrow\) \(\dfrac{b}{y}=\dfrac{c}{z}\left(1\right)\)
\(\Rightarrow\dfrac{az-cx}{y}=0\) \(\Rightarrow az=cx\) \(\Rightarrow\dfrac{a}{x}=\dfrac{c}{z}\left(2\right)\)
Từ (1) và (2) suy ra : \(\dfrac{a}{x}=\dfrac{b}{y}=\dfrac{c}{z}\)
Đúng 2
Bình luận (0)
cho các số a, b, c khác 0, \(\dfrac{bz-cy}{a}=\dfrac{cx-az}{a}=\dfrac{ay-bx}{c}\)cmr: \(\dfrac{x}{a}=\dfrac{y}{b}\)=\(\dfrac{z}{c}\)
Cho biết : \(\dfrac{bz-cy}{a}=\dfrac{cx-az}{b}=\dfrac{ay-bx}{c}\) với a,b,c \(\ne\) 0
Chứng minh rằng \(\dfrac{x}{a}=\dfrac{y}{b}=\dfrac{z}{c}\)
Ta có : \(\dfrac{bz-cy}{a}\text{=}\dfrac{cx-az}{b}\text{=}\dfrac{ay-bx}{c}\)
\(\Rightarrow\dfrac{a\left(bz-cy\right)}{a^2}\text{=}\dfrac{b\left(cx-az\right)}{b^2}\text{=}\dfrac{c\left(ay-bx\right)}{c^2}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có :
\(\dfrac{a\left(bz-cy\right)}{a^2}\text{=}\dfrac{b\left(cx-az\right)}{b^2}\text{=}\dfrac{c\left(ay-bx\right)}{c^2}\text{=}\dfrac{abz-acy+bcz-baz+cay-cbx}{a^2+b^2+c^2}\text{=}0\)
\(\Rightarrow\dfrac{bz-cy}{a}\text{=}0\Rightarrow bz\text{=}cy\)
\(\Rightarrow\dfrac{b}{c}\text{=}\dfrac{y}{z}\left(1\right)\)
\(\dfrac{cx-az}{b}\text{=}0\Rightarrow cx\text{=}az\)
\(\Rightarrow\dfrac{c}{a}\text{=}\dfrac{z}{x}\left(2\right)\)
Từ (1) và (2):
\(\Rightarrow dpcm\)
Đúng 3
Bình luận (0)
Cho các số a, b, c, x, y, z Thỏa mãn điều kiện: \(\dfrac{x}{a}=\dfrac{y}{b}=\dfrac{z}{c}\).Chứng minh rằng:
\(\dfrac{bz-cy}{a}=\dfrac{cx-az}{b}=\dfrac{ay-bx}{c}\)
Cho \(\dfrac{bz+cy}{x\left(-ax+by+cz\right)}=\dfrac{cx+az}{y\left(ax-by+cz\right)}=\dfrac{ay+bx}{z\left(ax+by-cz\right)}\)
CMR : \(\dfrac{ay+bx}{c}=\dfrac{bz+cy}{a}=\dfrac{cx+az}{b}\)
b) \(\dfrac{x}{a\left(b^2+c^2-a^2\right)}=\dfrac{y}{b\left(a^2+c^2-b^2\right)}=\dfrac{z}{c\left(a^2+b^2-c^2\right)}\)
cho \(\dfrac{x}{a}=\dfrac{y}{b}=\dfrac{z}{c}\).CMR:\(\dfrac{bz-cy}{a}=\dfrac{cx-az}{b}=\dfrac{ay-bx}{c}\)
Cho \(\dfrac{bz-cy}{a}=\dfrac{cx-az}{b}=\dfrac{ay-bx}{c}\).CMR \(\dfrac{x}{a}=\dfrac{y}{b}=\dfrac{z}{c}\)
10 người cùng cày trên 1 cánh đồng hết 10,5 h
a)Hỏi nếu 5 máy cùng cày trên 9 mảnh ruộng như thế hết bao nhiêu thời gian ,biết rằng năng xuất của 1 máy =15 người và cày 1 cánh đồng 3h
b)cho chu vi mảnh ruộng là 18 m , và chiều dài tỉ lệ với chiều rộng là 5:1 . hỏi giá tiền của phải trả cho người cày hết 9 mảnh ruộng đó là bao nhiêu tiền biết 1m2 phải trả 10000 đồng
Đúng 0
Bình luận (0)
làm hộ mk rồi mk giải cho mik lm bài này rồi
Đúng 0
Bình luận (0)
\(\dfrac{bz-cy}{a}=\dfrac{cx-az}{b}=\dfrac{ay-bx}{c}\)
CMR: \(\dfrac{x}{a}=\dfrac{y}{b}=\dfrac{z}{c}\)