Thực hiện phép tính :
A=\(\sqrt{x+2\sqrt{x-1}}-\sqrt{x-2\sqrt{x-1}}\)
Thực hiện phép tính : \(\sqrt{27}+\sqrt{48}-\sqrt{108}-\sqrt{12}\)
Rút gọn biểu thức : \(P=\left(\dfrac{1}{\sqrt{x}-1}-\dfrac{1}{\sqrt{x}+1}\right)\cdot\dfrac{x-2\sqrt{x}+1}{2}\) với \(x\ge0;x\ne1\)
1.\(\sqrt{27}+\sqrt{48}-\sqrt{108}-\sqrt{12}=3\sqrt{3}+4\sqrt{3}-6\sqrt{3}-2\sqrt{3}=-\sqrt{3}\)
2.\(P=\left(\dfrac{1}{\sqrt{x}-1}-\dfrac{1}{\sqrt{x}+1}\right).\dfrac{x-2\sqrt{x}+1}{2}\)
\(P=\left(\dfrac{\sqrt{x}+1-\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right).\dfrac{\left(\sqrt{x}-1\right)^2}{2}\)
\(P=\dfrac{2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}.\dfrac{\left(\sqrt{x}-1\right)^2}{2}\)
\(P=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\)
\(a,\sqrt{27}+\sqrt{48}-\sqrt{108}-\sqrt{12}\\ =3\sqrt{3}+4\sqrt{3}-6\sqrt{3}-2\sqrt{3}\\ =-\sqrt{3}\)
\(b,P=\left(\dfrac{1}{\sqrt{x}-1}-\dfrac{1}{\sqrt{x}+1}\right).\dfrac{x-2\sqrt{x}+1}{2}\\ =\dfrac{\left(\sqrt{x}+1\right)-\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}.\dfrac{\left(\sqrt{x}-1\right)^2}{2}\\ =\dfrac{\sqrt{x}+1-\sqrt{x}+1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}.\dfrac{\left(\sqrt{x}-1\right)^2}{2}\\ =\dfrac{2}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}.\dfrac{\left(\sqrt{x}-1\right)^2}{2}\\ =\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\)
Thực hiện các phép tính sau :
a. \(\dfrac{\sqrt{x}+1}{\sqrt{x}-2}+\dfrac{2\sqrt{x}}{\sqrt{x}+2}+\dfrac{2+5\sqrt{x}}{4-x}\)
b. \(\left(a^2b-3ab^2\right):\left(\dfrac{1}{2}ab\right)+\left(6b^3-5ab^2\right):b^2\)
Thực hiện các phép tính sau :
a. \(\dfrac{\sqrt{x}+1}{\sqrt{x}-2}+\dfrac{2\sqrt{x}}{\sqrt{x}+2}+\dfrac{2+5\sqrt{x}}{4-x}\)
b. \(\left(a^2b-3ab^2\right):\left(\dfrac{1}{2}ab\right)+\left(6b^3-5ab^2\right):b^2\)
\(a,=\dfrac{x+3\sqrt{x}+2+2x-4\sqrt{x}-2-5\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\\ =\dfrac{3x-6\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{3\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{3\sqrt{x}}{\sqrt{x}+2}\\ b,=2a-6b+6b-5a=-3a\)
1) Thực hiện phép tính
\(\sqrt{50}-3\sqrt{8}+\sqrt{32}\)
2) Giải các phương trình sau:
a)\(\sqrt{x^2-4x+4}=1\)
b)\(\sqrt{x^2-3x}-\sqrt{x-3}=0\)
1.
\(\sqrt{50}-3\sqrt{8}+\sqrt{32}=5\sqrt{2}-6\sqrt{2}+4\sqrt{2}=3\sqrt{2}\)
2.
a, ĐK: \(x\in R\)
\(pt\Leftrightarrow\sqrt{\left(x-2\right)^2}=1\)
\(\Leftrightarrow\left|x-2\right|=1\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=1\\x-2=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=1\end{matrix}\right.\)
b, ĐK: \(x\ge3\)
\(pt\Leftrightarrow\sqrt{x-3}\left(\sqrt{x}-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x-3}=0\\\sqrt{x}-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\left(tm\right)\\x=1\left(l\right)\end{matrix}\right.\)
Thực hiện phép tính :
a. \(\dfrac{4}{\sqrt{x}+1}+\dfrac{2}{1-\sqrt{x}}-\dfrac{\sqrt{x}-5}{x-1}\)
b. \(\left(\dfrac{x+1}{x+2}+\dfrac{x+2}{x+3}\right):\dfrac{x+3}{x+1}\)
\(a,=\dfrac{4\sqrt{x}-4-2\sqrt{x}-2-\sqrt{x}+5}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\left(x\ge0;x\ne1\right)\\ =\dfrac{\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{1}{\sqrt{x}+1}\\ b,=\dfrac{x^2+4x+3+x^2+4x+4}{\left(x+2\right)\left(x+3\right)}\cdot\dfrac{x+1}{x+3}\left(x\ne-1;x\ne-2;x\ne-3\right)\\ =\dfrac{\left(2x^2+8x+7\right)\left(x+1\right)}{\left(x+2\right)\left(x+3\right)^2}\)
Thực hiện phép tính :
a. \(\dfrac{4}{\sqrt{x}+1}+\dfrac{2}{1-\sqrt{x}}-\dfrac{\sqrt{x}-5}{x-1}\)
b. \(\left(\dfrac{x+1}{x+2}+\dfrac{x+2}{x+3}\right):\dfrac{x+3}{x+1}\)
\(a,\dfrac{4}{\sqrt{x}+1}+\dfrac{2}{1-\sqrt{x}}-\dfrac{\sqrt{x}-5}{x-1}\)
\(=\dfrac{4\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}-\dfrac{2\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}-\dfrac{\sqrt{x}-5}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{4\sqrt{x}-4}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}-\dfrac{2\sqrt{x}+2}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}-\dfrac{\sqrt{x}-5}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{4\sqrt{x}-4-2\sqrt{x}-2-\sqrt{x}+5}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{\sqrt{x}-1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{1}{\sqrt{x}+1}\)
\(b,\left(\dfrac{x+1}{x+2}+\dfrac{x+2}{x+3}\right):\dfrac{x+3}{x+1}\)
\(=\left(\dfrac{\left(x+1\right)\left(x+3\right)}{\left(x+2\right)\left(x+3\right)}+\dfrac{\left(x+2\right)^2}{\left(x+2\right)\left(x+3\right)}\right).\dfrac{x+1}{x+3}\)
\(=\left(\dfrac{x^2+4x+3}{\left(x+2\right)\left(x+3\right)}+\dfrac{x^2+4x+4}{\left(x+2\right)\left(x+3\right)}\right).\dfrac{x+1}{x+3}\)
\(=\dfrac{x^2+4x+3+x^2+4x+4}{\left(x+2\right)\left(x+3\right)}.\dfrac{x+1}{x+3}\)
\(=\dfrac{2x^2+8x+7}{\left(x+2\right)\left(x+3\right)}.\dfrac{x+1}{x+3}\)
\(=\dfrac{\left(2x^2+8x+7\right)\left(x+1\right)}{\left(x+2\right)\left(x+3\right)^2}\)
\(=\dfrac{\left(2x^2+8x+7\right).x+2x^2+8x+7}{\left(x+2\right)\left(x+3\right)^2}\)
\(=\dfrac{2x^3+8x^2+7x+2x^2+8x+7}{\left(x+2\right)\left(x+3\right)^2}\)
\(=\dfrac{2x^3+10x^2+15x+7}{\left(x+2\right)\left(x+3\right)^2}\)
a, cho A = \(\dfrac{\sqrt{x+1}}{\sqrt{x-3}}\). tìm x để A có giá trị nguyên ( x ϵ Z)
b, Thực hiện phép tính: {[(2\(\sqrt{2}\))\(^2\) : 2,4] x [5,25 : (\(\sqrt{7}\))\(^2\)]} : {[2\(\dfrac{1}{7}\) : \(\dfrac{\left(\sqrt{5}\right)^2}{7}\)] : [2\(^2\) : \(\dfrac{\left(2\sqrt{2}\right)^2}{\sqrt{81}}\)]}
a: Sửa đề: \(A=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\)
ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\x\ne9\end{matrix}\right.\)
Để A là số nguyên thì \(\sqrt{x}+1⋮\sqrt{x}-3\)
=>\(\sqrt{x}-3+4⋮\sqrt{x}-3\)
=>\(4⋮\sqrt{x}-3\)
=>\(\sqrt{x}-3\in\left\{1;-1;2;-2;4;-4\right\}\)
=>\(\sqrt{x}\in\left\{4;2;5;1;7;-1\right\}\)
=>\(\sqrt{x}\in\left\{4;2;5;1;7\right\}\)
=>\(x\in\left\{16;4;25;1;49\right\}\)
b: 
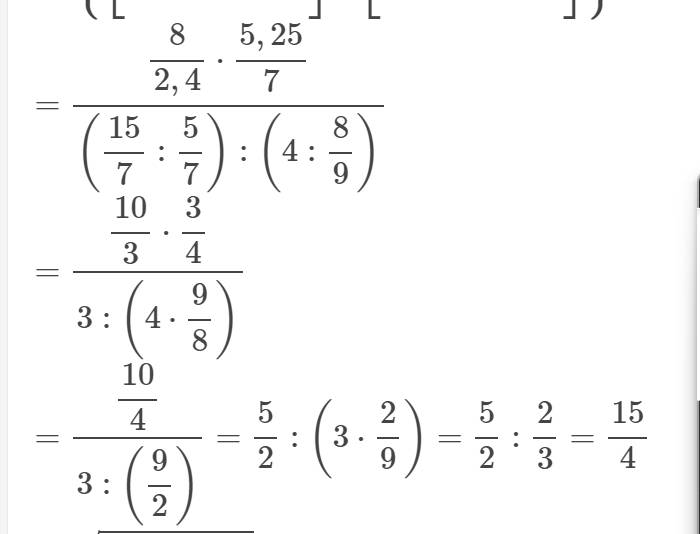
Bài 1:Tìm ĐKXĐ:
a.\(\sqrt{3x}\)
b.\(\sqrt{\dfrac{x-1}{x+3}}\)
Bài 2:Thực hiện phép tính:
C=\(\sqrt{5+2\sqrt{6}}-\sqrt{5-2\sqrt{6}}\)
Bài 3:
A=(1-\(\dfrac{\sqrt{x}}{\sqrt{x}+2}\)):(\(\dfrac{1}{\sqrt{x}-2}-\dfrac{2}{x-4}\)) với x>0;x≠4
a.Rút gọn A
b.Tính giá trị của A khi x =\(\dfrac{1}{4}\)
c. Chứng minh A<2
d.Tìm giá trị nguyên của x để A nguyên.
Trả lời giúp mình với ạ!Mình cảm ơn nhiều!
Bài 1:
a. ĐKXĐ: $3x\geq 0$
$\Leftrightarrow x\geq 0$
b. ĐKXĐ: $\frac{x-1}{x+3}\geq 0$
\(\Leftrightarrow \left[\begin{matrix} \left\{\begin{matrix} x-1\geq 0\\ x+3>0\end{matrix}\right.\\ \left\{\begin{matrix} x-1\leq 0\\ x+3< 0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} x\geq 1\\ x< -3\end{matrix}\right.\)
Bài 2:
\(C=\sqrt{5+2\sqrt{6}}-\sqrt{5-2\sqrt{6}}=\sqrt{2+2\sqrt{2.3}+3}-\sqrt{2-2\sqrt{2.3}+3}\)
\(=\sqrt{(\sqrt{2}+\sqrt{3})^2}-\sqrt{(\sqrt{2}-\sqrt{3})^2}\)
\(=|\sqrt{2}+\sqrt{3}|-|\sqrt{2}-\sqrt{3}|=(\sqrt{2}+\sqrt{3})-(\sqrt{3}-\sqrt{2})\)
\(=2\sqrt{2}\)
Bài 3:
a.
\(A=\frac{2}{\sqrt{x}+2}:\left[\frac{\sqrt{x}+2}{(\sqrt{x}-2)(\sqrt{x}+2)}-\frac{2}{(\sqrt{x}-2)(\sqrt{x}+2)}\right]\)
\(=\frac{2}{\sqrt{x}+2}:\frac{\sqrt{x}}{(\sqrt{x}-2)(\sqrt{x}+2)}=\frac{2}{\sqrt{x}+2}.\frac{(\sqrt{x}-2)(\sqrt{x}+2)}{\sqrt{x}}=\frac{2(\sqrt{x}-2)}{\sqrt{x}}\)
b. Khi $x=\frac{1}{4}$ thì $\sqrt{x}=\frac{1}{2}$.
Khi đó $A=\frac{2(\frac{1}{2}-2)}{\frac{1}{2}}=-6$
c.
$A=\frac{2(\sqrt{x}-2)}{\sqrt{x}}=2-\frac{4}{\sqrt{x}}$
$< 2$ do $\frac{4}{\sqrt{x}}>0$
Ta có đpcm
d. Với $x$ nguyên, để $A$ nguyên thì $\sqrt{x}$ là ước của $4$
$\Leftrightarrow \sqrt{x}\in\left\{1;2;4\right\}$
$\Rightarrow x\in\left\{1;4;16\right\}$ (đều tm)
\(p=\left(1+\frac{\sqrt{x}}{x+1}\right):\left(\frac{1}{\sqrt{x}-1}-\frac{2\sqrt{x}}{x\sqrt{x}+\sqrt{x}-x-1}\right)\rightarrow dk:x\ge0,x\ne1\)
a) thực hiện phép tính
b) tìm x để P<1
b) lấy kết quả rút gọn của câu A ta được
\(P=\frac{x+\sqrt{x}+1}{\sqrt{x}-1}< 1.=\frac{x+\sqrt{x}+1}{\sqrt{x}-1}-1< 0\)
\(P=\frac{x+\sqrt{x}+1-\sqrt{x}+1}{\sqrt{x}-1}=\frac{x+2}{\sqrt{x}-1}\)
đề bài cho x>=0 ta suy ra luôn
\(x+2>0\Leftrightarrow\sqrt{x}-1< 0\Leftrightarrow x< 1\)
vậy x <1 thì P < 1
\(P=\left(\frac{x+1+\sqrt{x}}{x+1}\right):\left(\frac{1}{\sqrt{x}-1}-\frac{2\sqrt{x}}{\sqrt{x}\left(x+1\right)-\left(x+1\right)}\right).\)
\(P=\left(\frac{x+1+\sqrt{x}}{x+1}\right):\left(\frac{1}{\sqrt{x-1}}-\frac{2\sqrt{x}}{\left(x+1\right)\left(\sqrt{x}-1\right)}\right)\)
\(P=\left(\frac{x+1+\sqrt{x}}{x+1}\right):\left(\frac{x+1-2\sqrt{x}}{\left(x+1\right)\left(\sqrt{x}-1\right)}\right)\)
\(P=\frac{\left(x+\sqrt{x}+1\right)}{\left(x+1\right)}:\frac{\left(\sqrt{x}-1\right)^2}{\left(x+1\right)\left(\sqrt{x}-1\right)}=\frac{\left(x+\sqrt{x}+1\right)}{\left(x+1\right)}.\frac{\left(x+1\right)}{\sqrt{x}-1}\)
\(P=\frac{x+\sqrt{x}+1}{\sqrt{x}-1}\)
1.thực hiện phép tính: \(\sqrt{4-2\sqrt3} \)-\(\dfrac{2}{\sqrt3+1}\)+\(\dfrac{\sqrt{3} -3}{\sqrt{3}-1}\)
2.cho biểu thức B=\(\dfrac{\sqrt{x}}{\sqrt{x}-3} \) + \(\dfrac{2\sqrt{x}-24}{x-9}\) với x ≥ 0, x≠9
a) rút gọn B
b) tìm giá trị của x để biểu thức B=5
Bài `1`
\(\sqrt{4-2\sqrt{3}}-\dfrac{2}{\sqrt{3}+1}+\dfrac{\sqrt{3}-3}{\sqrt{3}-1}\\ =\sqrt{3-2\sqrt{3}+1}-\dfrac{2\left(\sqrt{3}-1\right)}{3-1}-\dfrac{\sqrt{3}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}\\ =\sqrt{\left(\sqrt{3}\right)^2-2\cdot\sqrt{3}\cdot1+1^2}-\dfrac{2\left(\sqrt{3}-1\right)}{2}-\sqrt{3}\\ =\sqrt{\left(\sqrt{3}-1\right)^2}-\sqrt{3}+1-\sqrt{3}\\ =\sqrt{3}-1-\sqrt{3}+1-\sqrt{3}\\ =-\sqrt{3}\)
2:
a: \(B=\dfrac{\sqrt{x}}{\sqrt{x}-3}+\dfrac{2\sqrt{x}-24}{x-9}\)
\(=\dfrac{\sqrt{x}}{\sqrt{x}-3}+\dfrac{2\sqrt{x}-24}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}+3\right)+2\sqrt{x}-24}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{x+5\sqrt{x}-24}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{\left(\sqrt{x}+8\right)\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{\sqrt{x}+8}{\sqrt{x}+3}\)
b: B=5
=>\(5\left(\sqrt{x}+3\right)=\sqrt{x}+8\)
=>\(5\sqrt{x}+15=\sqrt{x}+8\)
=>\(4\sqrt{x}=-7\)(loại)
Vậy: \(x\in\varnothing\)