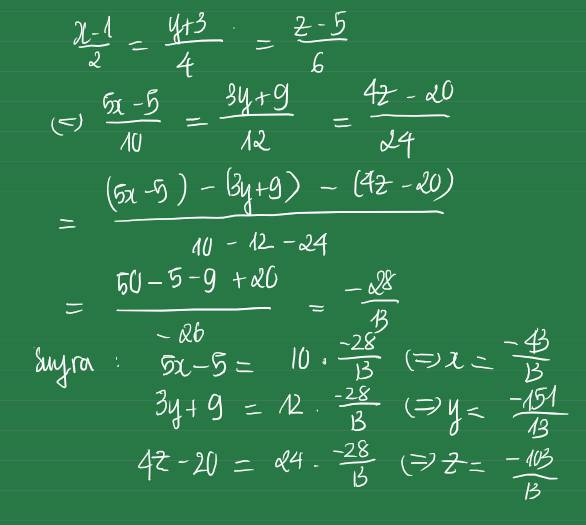\(\dfrac{x}{-2}=\dfrac{y}{3}\)

=>\(\dfrac{x}{-4}=\dfrac{y}{6}\)

mà \(\dfrac{y}{6}=\dfrac{z}{2}\)

nên \(\dfrac{x}{-4}=\dfrac{y}{6}=\dfrac{z}{2}\)

mà x+y+z=28

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{x}{-4}=\dfrac{y}{6}=\dfrac{z}{2}=\dfrac{x+y+z}{-4+6+2}=\dfrac{28}{4}=7\)

=>\(x=-4\cdot7=-28;y=6\cdot7=42;z=2\cdot7=14\)

7) vì \(\dfrac{x}{5}\)=\(\dfrac{y}{6}\)=\(\dfrac{z}{7}\)và x-y+z=36

Nên theo tính chất của dãy tỉ số bằng nhau ta có:

 \(\dfrac{x}{5}\)=\(\dfrac{y}{6}\)=\(\dfrac{z}{7}\)=\(\dfrac{x-y+z}{5-6+7}\)=\(\dfrac{36}{6}\)=6

 \(\Rightarrow\)x=6.5=30

     y=6.6=36

     z=6.7=42

vậy x=30,y=36,z=42

a) Áp dụng tính chất dãy tỉ số bằng nhau ta được:

X/3 = y/4 = x/3 + y/4 = 28/7 = 4

=> x = 4 × 3 = 12

=> y = 4 × 4 = 16

Vậy x = 12, y = 16

B) Áp dụng tính chất dãy tỉ số bằng nhau ta được:

X/2 = y/(-5) = x/2 - y/(-5) = (-7)/7 = -1

=> x = -1 × 2 = -2

=> y = -1 × -5 = 5

Vậy x = -2, y = 5

C) làm tương tự như bài a, b

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\Rightarrow\dfrac{x}{8}=\dfrac{y}{6}=\dfrac{z}{11}=k\)

\(\Rightarrow\left\{{}\begin{matrix}x=8k\\y=6k\\z=11k\end{matrix}\right.\)\(\Rightarrow xyz=528k^3=-528\Rightarrow k=-1\)

\(\Rightarrow\left\{{}\begin{matrix}x=8.\left(-1\right)=-8\\y=6.\left(-1\right)=-6\\z=11.\left(-1\right)=-11\end{matrix}\right.\)

Áp dụng t/c dtsbn:

\(\dfrac{x}{13}=\dfrac{y}{7}=\dfrac{z}{5}=\dfrac{x-y-z}{13-7-5}=\dfrac{6}{1}=6\)

\(\Rightarrow\left\{{}\begin{matrix}x=13.6=78\\y=13.7=91\\z=13.5=65\end{matrix}\right.\)

Áp dụng t/c dtsbn ta có:

\(\dfrac{x}{5}=\dfrac{y}{3}=\dfrac{z}{6}=\dfrac{x-y}{5-3}=\dfrac{4}{2}=2\)

\(\dfrac{x}{5}=2\Rightarrow x=10\\ \dfrac{y}{3}=2\Rightarrow y=6\\ \dfrac{z}{6}=2\Rightarrow z=12\)

Áp dụng t/c dtsbn:

\(\dfrac{x}{5}=\dfrac{y}{3}=\dfrac{z}{6}=\dfrac{x-y}{5-3}=2\)

\(\Rightarrow\left\{{}\begin{matrix}x=10\\y=6\\z=12\end{matrix}\right.\)

\(\dfrac{x-y}{5-3}=\dfrac{4}{2}=2\\ \)

=> \(\dfrac{x}{5}=5\cdot2=10\\ \)

=> \(\dfrac{x}{3}=3\cdot2=6\)

=>\(\dfrac{z}{6}=6\cdot2=12\)

Vậy...

Áp dụng t/c dtsbn:

\(\dfrac{x-1}{2}=\dfrac{y+3}{4}=\dfrac{z-5}{6}=\dfrac{3x-3}{6}=\dfrac{4y+12}{16}=\dfrac{5z-25}{30}=\dfrac{-3x+3-4y-12+5z-25}{-6-16+30}=\dfrac{50+3-12-25}{8}=\dfrac{16}{8}=2\\ \Rightarrow\left\{{}\begin{matrix}x-1=4\\y+3=8\\z-5=12\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=5\\y=5\\z=17\end{matrix}\right.\)

a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{x}{10}=\dfrac{y}{15}=\dfrac{z}{12}=\dfrac{x-y+z}{10-15+12}=\dfrac{-49}{7}=-7\)

Do đó: x=-70; y=-135; z=-84

a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

a) \(\left\{{}\begin{matrix}\dfrac{x}{2}=\dfrac{y}{3}\\\dfrac{y}{5}=\dfrac{z}{4}\end{matrix}\right.\)

 \(\Rightarrow\dfrac{x}{10}=\dfrac{y}{15}=\dfrac{z}{12}=\dfrac{x+z-y}{10+12-15}=-\dfrac{49}{7}=-7\)

\(\Rightarrow\left\{{}\begin{matrix}x=\left(-7\right).10=-70\\y=\left(-7\right).15=-105\\z=\left(-7\right).12=-84\end{matrix}\right.\)

b) \(\left\{{}\begin{matrix}\dfrac{x}{3}=\dfrac{y}{-2}\\\dfrac{x}{6}=\dfrac{z}{7}\end{matrix}\right.\)

\(\Rightarrow\dfrac{x}{6}=\dfrac{y}{-4}=\dfrac{z}{7}=\dfrac{3x}{18}=\dfrac{2y}{-8}=\dfrac{3x-z+2y}{18-7-8}=\dfrac{3}{3}=1\)

\(\Rightarrow\left\{{}\begin{matrix}x=1.6=6\\y=1.\left(-4\right)=-4\\z=1.7=7\end{matrix}\right.\)

a) \(\dfrac{x}{2}=\dfrac{y}{3}\Rightarrow\dfrac{x^2}{4}=\dfrac{y^2}{9}=\dfrac{x^2-y^2}{4-9}=\dfrac{-16}{-5}=\dfrac{16}{5}\)

\(\Rightarrow\left\{{}\begin{matrix}x^2=4.\dfrac{16}{5}\\y^2=9.\dfrac{16}{5}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=\pm\left(2.\dfrac{4}{\sqrt[]{5}}\right)=\pm\dfrac{8\sqrt[]{5}}{5}\\y=\pm\left(3.\dfrac{4}{\sqrt[]{5}}\right)=\pm\dfrac{12\sqrt[]{5}}{5}\end{matrix}\right.\)

\(\dfrac{y}{4}=\dfrac{z}{5}\Rightarrow z=\dfrac{5}{4}y=\dfrac{5}{4}.\left(\pm\dfrac{12\sqrt[]{5}}{5}\right)=\pm3\sqrt[]{5}\)

b) \(\left|2x+3\right|=x+2\)

\(\Rightarrow\left[{}\begin{matrix}2x+3=x+2\\2x+3=-x-2\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=-1\\3x=-5\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=-1\\3x=-\dfrac{5}{3}\end{matrix}\right.\)

Đính chính

Dòng cuối \(3x=-\dfrac{5}{3}\rightarrow x=-\dfrac{5}{3}\)