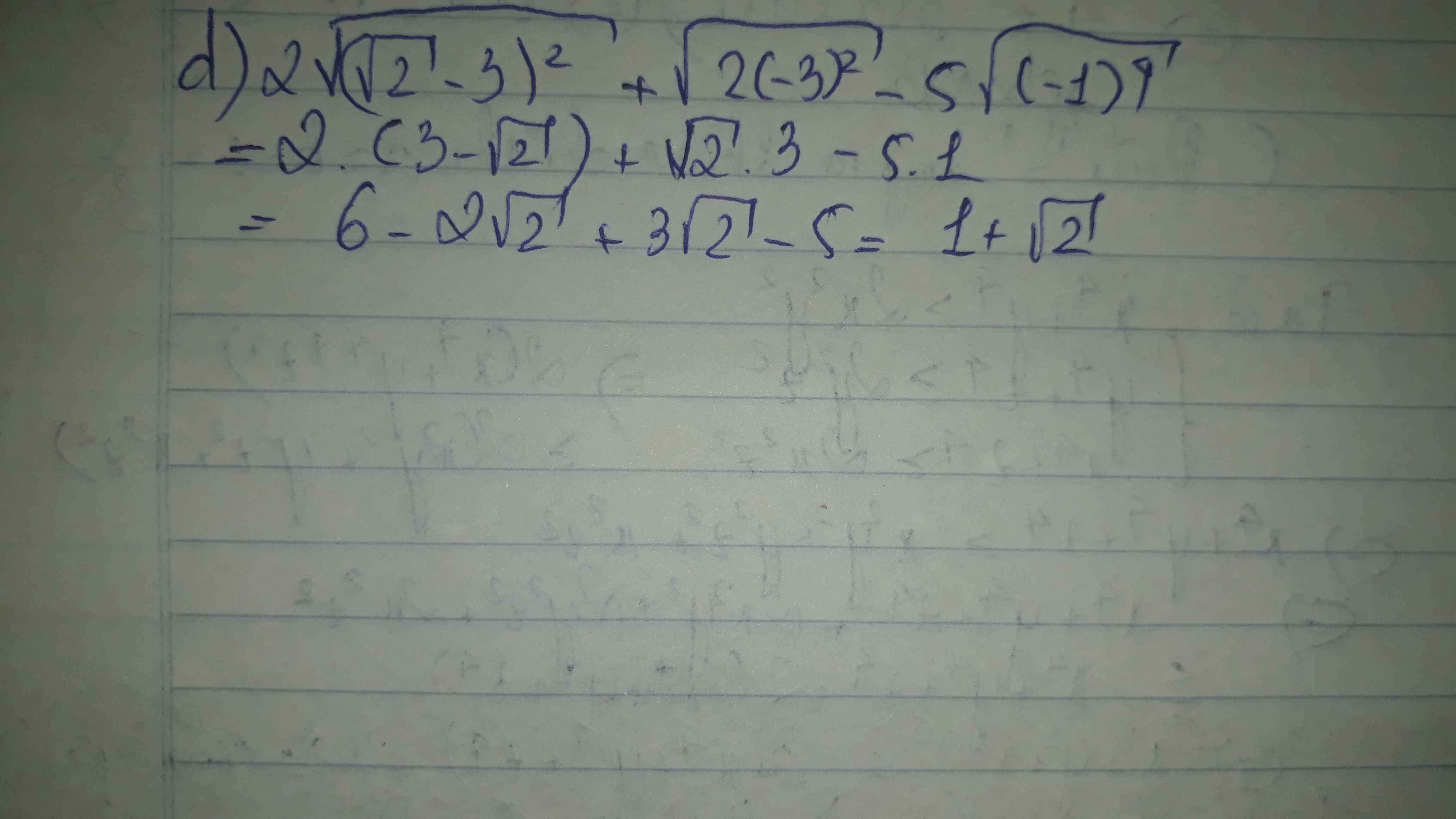Trong các số \(\sqrt{\left(-5\right)^2};\sqrt{5^2};-\sqrt{5^2};-\sqrt{\left(-5\right)^2}\), số nào là căn bậc hai số học của 25 ?

Những câu hỏi liên quan
Các số sau đây có căn bậc hai không?
a) A = \(\left(1-\dfrac{\sqrt{3}-1}{2}\right):\left(\dfrac{\sqrt{3}-1}{2}+2\right)\)
b) B = \(\left(\dfrac{\sqrt{6}-\sqrt{2}}{1-\sqrt{3}}-\dfrac{5}{\sqrt{5}}\right):\dfrac{1}{\sqrt{5}-\sqrt{2}}\)
a) \(A=\left(1-\dfrac{\sqrt{3}-1}{2}\right):\left(\dfrac{\sqrt{3}-1}{2}+2\right)\)
\(=\left(\dfrac{2}{2}-\dfrac{\sqrt{3}-1}{2}\right):\left(\dfrac{\sqrt{3}-1}{2}+\dfrac{4}{2}\right)\)
\(=\dfrac{2-\left(\sqrt{3}-1\right)}{2}:\dfrac{\left(\sqrt{3}-1\right)+4}{2}\)
\(=\dfrac{3-\sqrt{3}}{2}.\dfrac{2}{\sqrt{3}+3}\)
\(=\dfrac{\sqrt{3}\left(\sqrt{3}-1\right)}{\sqrt{3}\left(1+\sqrt{3}\right)}\)
\(=\dfrac{\left(\sqrt{3}-1\right)\left(\sqrt{3}-1\right)}{\left(\sqrt{3}+1\right)\left(\sqrt{3}-1\right)}\)
\(=\dfrac{\left(\sqrt{3}-1\right)^2}{2}\)
Vì \(\left\{{}\begin{matrix}\left(\sqrt{3}-1\right)^2>0\\2>0\end{matrix}\right.\) \(\Rightarrow\dfrac{\left(\sqrt{3}-1\right)^2}{2}>0\) hay A>0
=> A có căn bậc 2
Vậy......
b)\(B=\left(\dfrac{\sqrt{6}-\sqrt{2}}{1-\sqrt{3}}-\dfrac{5}{\sqrt{5}}\right):\dfrac{1}{\sqrt{5}-\sqrt{2}}\)
\(=\left(\dfrac{\sqrt{2}\left(\sqrt{3}-1\right)\left(1+\sqrt{3}\right)}{\left(1-\sqrt{3}\right)\left(1+\sqrt{3}\right)}-\sqrt{5}\right):\dfrac{\sqrt{5}+\sqrt{2}}{\left(\sqrt{5}-\sqrt{2}\right)\left(\sqrt{5}+\sqrt{2}\right)}\)
\(=\left(\dfrac{\sqrt{2}\left(3-1\right)}{1-3}-\sqrt{5}\right).\dfrac{5-2}{\sqrt{5}+\sqrt{2}}\)
\(=\left(-\sqrt{2}-\sqrt{5}\right).\dfrac{3}{\sqrt{5}+\sqrt{2}}\)
\(=-\left(\sqrt{2}+\sqrt{5}\right).\dfrac{3}{\sqrt{5}+\sqrt{2}}\)
\(=-3\)
Vì -3 < 0 hay B < 0
=> B không có căn bậc 2
Vậy.....
Đúng 1
Bình luận (0)
Tính tổng sau:Afrac{1}{left[sqrt[3]{2}right]}+frac{1}{left[sqrt[3]{3}right]}+frac{1}{left[sqrt[3]{4}right]}+frac{1}{left[sqrt[3]{5}right]}+frac{1}{left[sqrt[3]{6}right]}+frac{1}{left[sqrt[3]{7}right]}+frac{1}{left[sqrt[3]{9}right]}+...+frac{1}{left[sqrt[3]{2012^3-1}right]}(trong tổng trên không có các số dạng frac{1}{left[sqrt[3]{n}right]} với n là lập phương 1 số nguyên,ví dụ:1 và 8)
Đọc tiếp
Tính tổng sau:
\(A=\frac{1}{\left[\sqrt[3]{2}\right]}+\frac{1}{\left[\sqrt[3]{3}\right]}+\frac{1}{\left[\sqrt[3]{4}\right]}+\frac{1}{\left[\sqrt[3]{5}\right]}+\frac{1}{\left[\sqrt[3]{6}\right]}+\frac{1}{\left[\sqrt[3]{7}\right]}+\frac{1}{\left[\sqrt[3]{9}\right]}+...+\frac{1}{\left[\sqrt[3]{2012^3-1}\right]}\)
(trong tổng trên không có các số dạng \(\frac{1}{\left[\sqrt[3]{n}\right]}\) với n là lập phương 1 số nguyên,ví dụ:1 và 8)
Ta có từ n3 + 1 đến (n + 1)3 - 1 có
(n + 1)3 - 1 - n3 - 1 + 1 = 3n2 + 3n số có phần nguyên bằng n
Áp dụng vào cái ban đầu ta có
\(=\frac{3.1^2+3.1}{1}+\frac{3.2^2+3.2}{2}+...+\frac{3.2011^2+3.2011}{2011}\)
= 3.1 + 3 + 3.2 + 3 + ...+ 3.2011 + 3
= 3.2011 + 3(1 + 2 +...+ 2011)
= 6075231
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho x,y,z là các số thực dương thỏa mãn đẳng thức xy+yz+zx=5. Tìm giá trị nhỏ nhất của biểu thức
\(P=\frac{3x+3y+3z}{\sqrt{6\left(x^2+5\right)}+\sqrt{6\left(y^2+5\right)}+\sqrt{6\left(z^2+5\right)}}\)
Mình nghĩ phần phân thức là $3x+3y+2z$ thay vì $3x+3y+3z$. Nếu là vậy thì bạn tham khảo lời giải tại link sau:
Đúng 1
Bình luận (2)
Tính giá trị các biểu thức
A = \(\sqrt{\left(5-\sqrt{3}\right)^2}+\sqrt{\left(2-\sqrt{3}\right)^2}\)
B = \(\sqrt{\left(3-\sqrt{2}\right)^2}-\sqrt{\left(1-\sqrt{2}\right)^2}\)
C = \(\sqrt{\left(3+\sqrt{7}\right)^2}-\sqrt{\left(2-\sqrt{7}\right)^2}\)
D = \(\sqrt{4-2\sqrt{3}}+\sqrt{7+4\sqrt{3}}\)
`A=sqrt{(5-sqrt3)^2}+sqrt{(2-sqrt3)^2}`
`=5-sqrt3+2-sqrt3`
`=7-2sqrt3`
`B=sqrt{(3-sqrt2)^2}-sqrt{(1-sqrt2)^2}`
`=3-sqrt2-(sqrt2-1)`
`=4-2sqrt2`
`C=sqrt{(3+sqrt7)^2}-sqrt{(2-sqrt7)^2}`
`=3+sqrt7-(sqrt7-2)`
`=5`
`D=sqrt{4-2sqrt3}+sqrt{7+4sqrt3}`
`=sqrt{3-2sqrt3+1}+sqrt{4+2.2.sqrt3+3}`
`=sqrt{(sqrt3-1)^2}+sqrt{(2+sqrt3)^2}`
`=sqrt3-1+2+sqrt3=1+2sqrt3`
Đúng 2
Bình luận (0)
\(A=\left|5-\sqrt{3}\right|+\left|2-\sqrt{3}\right|=5-\sqrt{3}+2-\sqrt{3}=7-2\sqrt{3}\)
\(B=\left|3-\sqrt{2}\right|-\left|1-\sqrt{2}\right|=3-\sqrt{2}-\sqrt{2}+1=4-2\sqrt{2}\)
\(C=\left|3+\sqrt{7}\right|-\left|2-\sqrt{7}\right|=3+\sqrt{7}-\sqrt{7}+2=5\)
\(D=\sqrt{3-2\sqrt{3}+1}+\sqrt{4+2.2\sqrt{3}+3}\)
\(=\sqrt{\left(\sqrt{3}-1\right)^2}+\sqrt{\left(2+\sqrt{3}\right)^2}=\left|\sqrt{3}-1\right|+\left|2+\sqrt{3}\right|\)
\(=\sqrt{3}-1+2+\sqrt{3}=1+2\sqrt{3}\)
Đúng 2
Bình luận (0)
Đưa một thừa số vào trong dấu căn: \(x\sqrt{\dfrac{2}{x}}\left(x>0\right)\); \(x\sqrt{\dfrac{2}{5}}\); \(\left(x-5\right)\sqrt{\dfrac{x}{25-x^2}}\); \(x\sqrt{\dfrac{7}{x^2}}\)
\(x\sqrt{\dfrac{2}{x}}=\sqrt{x^2\cdot\dfrac{2}{x}}=\sqrt{2x}\)
\(x\sqrt{\dfrac{2}{5}}=\sqrt{\dfrac{2}{5}\cdot x^2}=\sqrt{\dfrac{2x^2}{5}}\)
\(\left(x-5\right)\cdot\sqrt{\dfrac{x}{25-x^2}}=\sqrt{\left(x-5\right)^2\cdot\dfrac{x}{-\left(x-5\right)\left(x+5\right)}}=\sqrt{-\dfrac{x\left(x-5\right)}{x+5}}\)
\(x\sqrt{\dfrac{7}{x^2}}=\sqrt{x^2\cdot\dfrac{7}{x^2}}=\sqrt{7}\)
Đúng 1
Bình luận (0)
Điểm nào sau đây thuộc đồ thị hàm số \(y=\left(\sqrt{5}-2\right)x+2\)
A. M\(\left(0;\sqrt{5}-2\right)\)
B. P\(\left(\sqrt{5}+2;3\right)\)
C. N\(\left(1;\sqrt{5}+2\right)\)
D. Q\(\left(-1;\sqrt{5}\right)\)
chứng minh \(S_n-2=\left(\left(\frac{\sqrt{5}+1}{2}\right)^n-\left(\frac{\sqrt{5}-1}{2}\right)^n\right)^2\) .Tìm tất cả các số n để \(S_n-2\)là số chính phương
Chứng minh rằng các số sau đây là số nguyên:
A = \(\sqrt{\sqrt{5}-\sqrt{3-\sqrt{29-12\sqrt{5}}}}\)
B = \(\frac{\left(5+2\sqrt{6}\right)\left(49-20\sqrt{6}\right)\sqrt{5-2\sqrt{6}}}{9\sqrt{3}-11\sqrt{2}}\)
Trả lời:
\(A=\sqrt{\sqrt{5}-\sqrt{3-\sqrt{29-12\sqrt{5}}}}\)
\(A=\sqrt{\sqrt{5}-\sqrt{3-\sqrt{20-12\sqrt{5}+9}}}\)
\(A=\sqrt{\sqrt{5}-\sqrt{3-\sqrt{\left(2\sqrt{5}-3\right)^2}}}\)
\(A=\sqrt{\sqrt{5}-\sqrt{3-2\sqrt{5}+3}}\)
\(A=\sqrt{\sqrt{5}-\sqrt{6-2\sqrt{5}}}\)
\(A=\sqrt{\sqrt{5}-\sqrt{5-2\sqrt{5}+1}}\)
\(A=\sqrt{\sqrt{5}-\sqrt{\left(\sqrt{5}-1\right)^2}}\)
\(A=\sqrt{\sqrt{5}-\sqrt{5}+1}\)
\(A=\sqrt{1}\)
\(A=1\)
\(B=\frac{\left(5+2\sqrt{6}\right).\left(49-20\sqrt{6}\right).\sqrt{5-2\sqrt{6}}}{9\sqrt{3}-11\sqrt{2}}\)
\(B=\frac{\left(3+2\sqrt{6}+2\right).\left(49-20\sqrt{6}\right).\sqrt{3-2\sqrt{6}+2}}{9\sqrt{3}-11\sqrt{2}}\)
\(B=\frac{\left(\sqrt{3}+\sqrt{2}\right)^2.\left(49-20\sqrt{6}\right).\sqrt{\left(\sqrt{3}-\sqrt{2}\right)^2}}{9\sqrt{3}-11\sqrt{2}}\)
\(B=\frac{\left(\sqrt{3}+\sqrt{2}\right)^2.\left(49-20\sqrt{6}\right).\left(\sqrt{3}-\sqrt{2}\right)}{9\sqrt{33}-11\sqrt{2}}\)
\(B=\frac{\left(\sqrt{3}+\sqrt{2}\right).\left(\sqrt{3}-\sqrt{2}\right).\left(\sqrt{3}+\sqrt{2}\right).\left(49-20\sqrt{6}\right)}{9\sqrt{3}-11\sqrt{2}}\)
\(B=\frac{\left(3-2\right).\left(49\sqrt{3}-60\sqrt{2}+49\sqrt{2}-40\sqrt{3}\right)}{9\sqrt{3}-11\sqrt{2}}\)
\(B=\frac{1.\left(9\sqrt{3}-11\sqrt{2}\right)}{9\sqrt{3}-11\sqrt{2}}\)
\(B=1\)
a) Ta có: \(\sqrt{29-12\sqrt{5}}=\sqrt{20-12\sqrt{5}+9}=\sqrt{\left(2\sqrt{5}-3\right)^2}\)
\(=\left|2\sqrt{5}-3\right|=2\sqrt{5}-3\)
\(\Rightarrow\sqrt{3-\sqrt{29-12\sqrt{5}}}=\sqrt{3-\left(2\sqrt{5}-3\right)}=\sqrt{3-2\sqrt{5}+3}\)
\(=\sqrt{6-2\sqrt{5}}=\sqrt{5-2\sqrt{5}+1}=\sqrt{\left(\sqrt{5}-1\right)^2}\)
\(=\left|\sqrt{5}-1\right|=\sqrt{5}-1\)
\(\Leftrightarrow A=\sqrt{\sqrt{5}-\sqrt{3-\sqrt{29-12\sqrt{5}}}}=\sqrt{\sqrt{5}-\left(\sqrt{5}-1\right)}\)
\(=\sqrt{\sqrt{5}-\sqrt{5}+1}=\sqrt{1}=1\)( đpcm )
Rút gọn các biểu thức sau:
d) \(2\sqrt{\left(\sqrt{2}-3\right)^2}+\sqrt{2\left(-3\right)^2}-5\sqrt{\left(-1\right)^4}\)
\(=2\left|3-\sqrt{2}\right|+\sqrt{18}-5.1=6-2\sqrt{2}+3\sqrt{2}-5\)
\(=1+\sqrt{2}\)
Đúng 1
Bình luận (0)