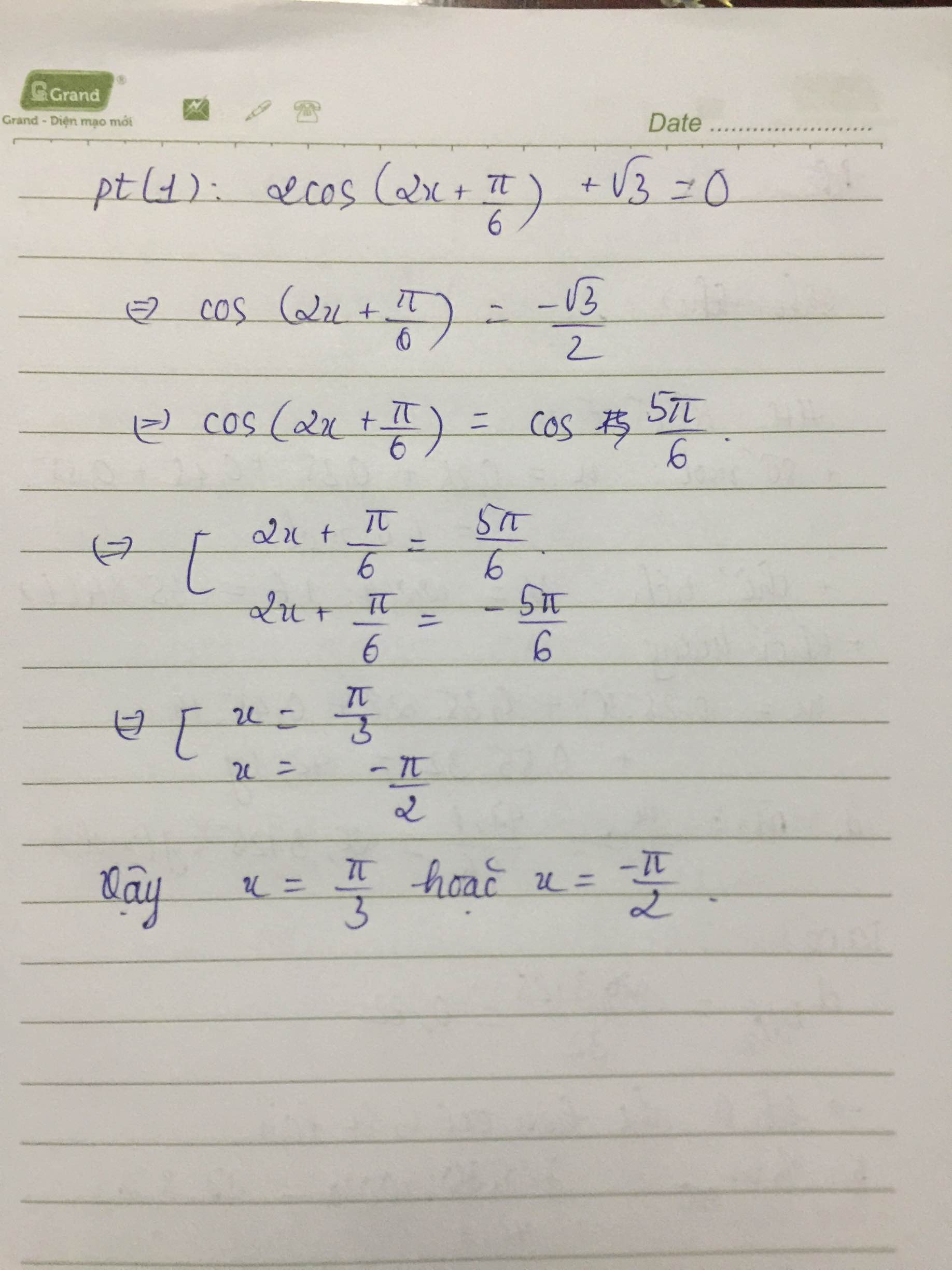a: ĐKXĐ: 2*sin x+1<>0

=>sin x<>-1/2

=>x<>-pi/6+k2pi và x<>7/6pi+k2pi

b: ĐKXĐ: \(\dfrac{1+cosx}{2-cosx}>=0\)

mà 1+cosx>=0

nên 2-cosx>=0

=>cosx<=2(luôn đúng)

c ĐKXĐ: tan x>0

=>kpi<x<pi/2+kpi

d: ĐKXĐ: \(2\cdot cos\left(x-\dfrac{pi}{4}\right)-1< >0\)

=>cos(x-pi/4)<>1/2

=>x-pi/4<>pi/3+k2pi và x-pi/4<>-pi/3+k2pi

=>x<>7/12pi+k2pi và x<>-pi/12+k2pi

e: ĐKXĐ: x-pi/3<>pi/2+kpi và x+pi/4<>kpi

=>x<>5/6pi+kpi và x<>kpi-pi/4

f: ĐKXĐ: cos^2x-sin^2x<>0

=>cos2x<>0

=>2x<>pi/2+kpi

=>x<>pi/4+kpi/2

1.

\(\Leftrightarrow cos\left(2x+\dfrac{4\pi}{3}\right)=0\)

\(\Leftrightarrow2x+\dfrac{4\pi}{3}=\dfrac{\pi}{2}+k\pi\)

\(\Leftrightarrow2x=-\dfrac{5\pi}{6}+k\pi\)

\(\Leftrightarrow x=-\dfrac{5\pi}{12}+\dfrac{k\pi}{2}\)

b.

\(\Leftrightarrow2+2cos\left(2x+\dfrac{\pi}{3}\right)-3=0\)

\(\Leftrightarrow cos\left(2x+\dfrac{\pi}{3}\right)=\dfrac{1}{2}\)

\(\Leftrightarrow\left[{}\begin{matrix}2x+\dfrac{\pi}{3}=\dfrac{\pi}{3}+k2\pi\\2x+\dfrac{\pi}{3}=-\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=k\pi\\x=-\dfrac{\pi}{3}+k\pi\end{matrix}\right.\)

c.

\(\Leftrightarrow cos\left(2x-\dfrac{\pi}{6}\right)=\dfrac{\sqrt{3}}{2}\)

\(\Leftrightarrow\left[{}\begin{matrix}2x-\dfrac{\pi}{6}=\dfrac{\pi}{6}+k2\pi\\2x-\dfrac{\pi}{6}=-\dfrac{\pi}{6}+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k\pi\\x=k\pi\end{matrix}\right.\)

\(A=\dfrac{\sqrt{2}.cosx-2cos\left(\dfrac{\pi}{4}+x\right)}{-\sqrt{2}.sinx+2sin\left(\dfrac{\pi}{4}+x\right)}\)

\(=\dfrac{\sqrt{2}.cosx-2\left(cos\dfrac{\pi}{4}.cosx-sin\dfrac{\pi}{4}.sinx\right)}{-\sqrt{2}.sinx+2\left(sin\dfrac{\pi}{4}.cosx+cos\dfrac{\pi}{4}.sinx\right)}\)

\(=\dfrac{\sqrt{2}.cosx-\sqrt{2}.cosx+\sqrt{2}.sinx}{-\sqrt{2}.sinx+\sqrt{2}.cosx+\sqrt{2}.sinx}\)

\(=\dfrac{\sqrt{2}.sinx}{\sqrt{2}.cosx}=tanx\)

a.

\(y'=-\dfrac{3}{2}x^3+\dfrac{6}{5}x^2-x+5\)

b.

\(y'=\dfrac{\left(x^2+4x+5\right)'}{2\sqrt{x^2+4x+5}}=\dfrac{2x+4}{2\sqrt{x^2+4x+5}}=\dfrac{x+2}{\sqrt{x^2+4x+5}}\)

c.

\(y=\left(3x-2\right)^{\dfrac{1}{3}}\Rightarrow y'=\dfrac{1}{3}\left(3x-2\right)^{-\dfrac{2}{3}}=\dfrac{1}{3\sqrt[3]{\left(3x-2\right)^2}}\)

d.

\(y'=2\sqrt{x+2}+\dfrac{2x-1}{2\sqrt{x+2}}=\dfrac{6x+7}{2\sqrt{x+2}}\)

e.

\(y'=3sin^2\left(\dfrac{\pi}{3}-5x\right).\left[sin\left(\dfrac{\pi}{3}-5x\right)\right]'=-15sin^2\left(\dfrac{\pi}{3}-5x\right).cos\left(\dfrac{\pi}{3}-5x\right)\)

g.

\(y'=4cot^3\left(\dfrac{\pi}{6}-3x\right)\left[cot\left(\dfrac{\pi}{3}-3x\right)\right]'=12cot^3\left(\dfrac{\pi}{6}-3x\right).\dfrac{1}{sin^2\left(\dfrac{\pi}{3}-3x\right)}\)

PT \(\Leftrightarrow-2\left(1-2.sin^2\dfrac{x}{2}\right)-\sqrt{3}.cos2x=-1+2\left(cosx.cos\dfrac{3\pi}{4}-sinx.sin\dfrac{3\pi}{4}\right)^2\)

\(\Leftrightarrow-2.cosx-\sqrt{3}.cos2x=-1+2\left(cosx.-\dfrac{\sqrt{2}}{2}-sinx.\dfrac{\sqrt{2}}{2}\right)^2\)

\(\Leftrightarrow-2cosx-\sqrt{3}.cos2x=-1+\left(sinx+cosx\right)^2\)

\(\Leftrightarrow-2cosx=2sinx.cosx+\sqrt{3}cos2x\)

\(\Leftrightarrow-2cosx=sin2x+\sqrt{3}cos2x\)

\(\Leftrightarrow cos\left(\pi-x\right)=\dfrac{1}{2}.sin2x+\dfrac{\sqrt{3}}{2}.cos2x\)

\(\Leftrightarrow cos\left(\pi-x\right)=sin\left(2x+\dfrac{\pi}{3}\right)\)

\(\Leftrightarrow cos\left(\pi-x\right)=cos\left(\dfrac{\pi}{6}-2x\right)\)

\(\Leftrightarrow\left[{}\begin{matrix}\pi-x=\dfrac{\pi}{6}-2x+k2\pi\\\pi-x=-\dfrac{\pi}{6}+2x+k2\pi\end{matrix}\right.\) ( k nguyên )

\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{5\pi}{6}+k2\pi\\x=\dfrac{7\pi}{18}-\dfrac{k2\pi}{3}\end{matrix}\right.\) ( k nguyên )

Vậy...