Tìm GTLN: 3-4x-x2

Những câu hỏi liên quan
Tìm GTLN,GTNN của bt:
A=4x+3 / x2 +1
\(A=\dfrac{-x^2-1+x^2+4x+4}{x^2+1}=-1+\dfrac{\left(x+2\right)^2}{x^2+1}\ge-1\)
\(A_{min}=-1\) khi \(x=-2\)
\(A=\dfrac{4x^2+4-4x^2+4x-1}{x^2+1}=4-\dfrac{\left(2x-1\right)^2}{x^2+1}\le4\)
\(A_{max}=4\) khi \(x=\dfrac{1}{2}\)
Đúng 1
Bình luận (1)
Tìm GTLN,GTNN của bt:
A=3-4x / x2 +1
\(A=\dfrac{-x^2-1+x^2-4x+4}{x^2+1}=-1+\dfrac{\left(x-2\right)^2}{x^2+1}\ge-1\)
\(A_{min}=-1\) khi \(x=2\)
\(A=\dfrac{4x^2+4-4x^2-4x-1}{x^2+1}=4-\dfrac{\left(2x+1\right)^2}{x^2+1}\le4\)
\(A_{max}=4\) khi \(x=-\dfrac{1}{2}\)
Đúng 1
Bình luận (1)
. Tìm GTLN, GTNN của biểu thức:1) Tìm GTNN của biểu thức: a) A x2 - 7x +11.b) D x - 2 + x - 3 .c) C 3 - 4x .x2 +1d) B -5 .x2 - 4x + 7e) x2 - x +1 .M + x +1x2f) P x 1 x 2 x 3 x 6 .2) Tìm GTLN của biểu thức 2x 2 + 4x + 9 b)A x 2 + 2x + 4 . a)B −5 x 2+ 22 x − 25 2x 2 + 4x + 9 x 2+ 4 x + 4b)A x 2 + 2x + 4 . c) C (x2 - 3x +1)(21+ 3x - x2 ) .d) D 6x - 8 .x2 +1
Đọc tiếp
. Tìm GTLN, GTNN của biểu thức:
1) Tìm GTNN của biểu thức:
a) A = x2 - 7x +11. | b) D = x - 2 + x - 3 . |
c) C = 3 - 4x . x2 +1 | d) B = -5 . x2 - 4x + 7 |
e) x2 - x +1 . M = + x +1 x2 | f) P x 1 x 2 x 3 x 6 . |
2) Tìm GTLN của biểu thức
|
| 2x 2 + 4x + 9 |
|
b) | A = x 2 + 2x + 4 . | ||
|
| ||||||||||||||||||||
c) C = (x2 - 3x +1)(21+ 3x - x2 ) . | d) D = 6x - 8 . x2 +1 | ||||||||||||||||||||
1:
a: =x^2-7x+49/4-5/4
=(x-7/2)^2-5/4>=-5/4
Dấu = xảy ra khi x=7/2
b: =x^2+x+1/4-13/4
=(x+1/2)^2-13/4>=-13/4
Dấu = xảy ra khi x=-1/2
e: =x^2-x+1/4+3/4=(x-1/2)^2+3/4>=3/4
Dấu = xảy ra khi x=1/2
f: x^2-4x+7
=x^2-4x+4+3
=(x-2)^2+3>=3
Dấu = xảy ra khi x=2
2:
a: A=2x^2+4x+9
=2x^2+4x+2+7
=2(x^2+2x+1)+7
=2(x+1)^2+7>=7
Dấu = xảy ra khi x=-1
b: x^2+2x+4
=x^2+2x+1+3
=(x+1)^2+3>=3
Dấu = xảy ra khi x=-1
Đúng 0
Bình luận (0)
tìm GTLN/GTNN: x2 - 4x +7
\(x^2-4x+7\)
⇔ \(\left(x^2-4x+4\right)+3\)
⇔ \(\left(x-2\right)^2+3\)
Vì \(\left(x-2\right)^2\ge0\) ⇒ \(\left(x-2\right)^2+3\ge3\)
Vậy GTNN của A là 3 khi x =2
Đúng 0
Bình luận (0)
\(x^2-4x+7\)
\(=x^2-4x+4+3\)
\(=\left(x-2\right)^2+3\ge3\forall x\)
Dấu '=' xảy ra khi x=2
Đúng 0
Bình luận (0)
tìm GTLN của F= 4x - x2 + 1
\(F=-x^2+2.x.2-4+5=-\left(x^2-4x+4\right)+5\)
\(=-\left(x-2\right)^2+5\)
Thấy : \(\left(x-2\right)^2\ge0\)
\(\Rightarrow5-\left(x-2\right)^2\le5\)
Vậy MaxF = 5 tại x = 2 .
Đúng 0
Bình luận (0)
tìm GTLN của:
A=3x2+12x+17/x2+4x+5
\(A=\dfrac{3x^2+12x+17}{x^2+4x+5}=\dfrac{3\left(x^2+4x+5\right)+2}{x^2+4x+5}=3+\dfrac{2}{x^2+4x+5}\)
Ta có: \(x^2+4x+5=x^2+4x+4+1=\left(x+2\right)^2+1\ge1\)
\(\Rightarrow\dfrac{2}{x^2+4x+5}\le2\Rightarrow A\le3+2=5\)
\(\Rightarrow A_{max}=5\) khi \(x=-2\)
Đúng 3
Bình luận (3)
đề thế này á?
\(A=3x^2+12x+\dfrac{17}{x^2}+4x+5\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
tìm GTNN và GTLN của biểu thức
A = x2 - 4x +1
\(A=\left(x^2-4x+4\right)-3=\left(x-2\right)^2-3\ge-3\\ A_{min}=-3\Leftrightarrow x=2\)
Biểu thức A ko có max
Đúng 1
Bình luận (1)
tìm GTLN của biểu thức
A=-2x2 x2+4x-1
giúp mik với
Tìm GTLN của hàm số
y
x
2
-
x
+
4
x
-
1
trên
-
4
;
0
Đọc tiếp
Tìm GTLN của hàm số y = x 2 - x + 4 x - 1 trên - 4 ; 0
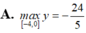
![]()
![]()
![]()
A= -x2 + 4x -8
Tìm GTLN ( giá trị lớn nhất của A)
`#3107.101107`
`A = -x^2 + 4x - 8`
`= -(x^2 - 4x + 8)`
`= - [ (x^2 - 2*x*2 + 2^2) + 4]`
`= - [ (x - 2)^2 + 4]`
`= -(x-2)^2 - 4`
Vì `-(x - 2)^2 \le 0` `AA` `x`
`=> -(x - 2)^2 - 4 \ge 0` `AA` `x`
Vậy, GTLN của A là `-4` khi `(x - 2)^2 = 0`
`<=> x - 2 = 0`
`<=> x = 2.`
Đúng 0
Bình luận (0)
A = -x² + 4x - 8
= -(x² - 4x + 8)
= -(x² - 4x + 4 + 4)
= -[(x - 2)² + 4]
= -(x - 2)² - 4
Do (x - 2)² ≥ 0 với mọi x R
⇒ -(x - 2)² ≤ 0 với mọi x ∈ R
⇒ -(x - 2)² - 4 ≤ -4 với mọi x ∈ R
Vậy GTLN của A là -4 khi x = 2
Đúng 0
Bình luận (0)



























