Tính các tích phân sau:
a) ; b)
c)
Bài 1: Tính khối lượng của các chất sau:
a. 0,25 mol CuO
b. 13,44 lít khí SO3 (đktc)
c. 1,2.1023 phân tử MgO
Bài 2: Tính khối thể tích (đktc) của các chất khí sau:
a. 0,3 mol CO2
b. 1,6 gam khí SO3
c. 0,3.1023 phân tử CO
Bài 3: Tính tỉ khối của các chất khí sau:
a. H2so với SO2
b. O2 so với không khí
Bài 4:Tính khối lượng mol của khí A, biết tỉ khối của khí O2 so với khí A bằng 1/2
. Tính thể tích khí oxi (đktc) điều chế được trong các trường hợp sau:
a) Nhiệt phân hoàn toàn 63,2 gam KMnO4
b) Nhiệt phân hoàn toàn 24,5 gam KClO3
\(pthh:\)
\(2KMnO_4\overset{t^o}{--->}K_2MnO_4+MnO_2+O_2\uparrow\left(1\right)\)
\(2KClO_3\xrightarrow[MnO_2]{t^o}2KCl+3O_2\uparrow\left(2\right)\)
a. Ta có: \(n_{KMnO_4}=\dfrac{63,2}{158}=0,4\left(mol\right)\)
Theo PT(1): \(n_{O_2}=\dfrac{1}{2}.0,4=0,2\left(mol\right)\)
\(\Rightarrow V_{O_2}=0,2.22,4=4,48\left(lít\right)\)
b. Ta có: \(n_{KClO_3}=\dfrac{24,5}{122,5}=0,2\left(mol\right)\)
Theo PT(2): \(n_{O_2}=\dfrac{3}{2}.0,2=0,3\left(mol\right)\)
\(\Rightarrow V_{O_2}=0,3.22,4=6,72\left(lít\right)\)
Tính các tích phân sau:
a) \(\int_0^1x^3\sqrt{1-x^2}dx\)
b) \(\int_1^2\dfrac{dx}{x^2-2x+2}\)
c) \(\int_1^2\dfrac{dx}{\sqrt{4-x^2}}\)
d) \(\int_0^1x\sqrt{x^2+1}dx\)
a.
Đặt \(\sqrt{1-x^2}=u\Rightarrow x^2=1-u^2\Rightarrow xdx=-udu\)
\(\left\{{}\begin{matrix}x=0\Rightarrow u=1\\x=1\Rightarrow u=0\end{matrix}\right.\)
\(\Rightarrow I=\int\limits^0_1\left(1-u^2\right).u.\left(-udu\right)=\int\limits^1_0\left(u^2-u^4\right)du=\left(\dfrac{1}{3}u^3-\dfrac{1}{5}u^5\right)|^1_0\)
\(=\dfrac{2}{15}\)
b.
\(\int\limits^2_1\dfrac{dx}{x^2-2x+2}=\int\limits^2_1\dfrac{dx}{\left(x-1\right)^2+1}\)
Đặt \(x-1=tanu\Rightarrow dx=\dfrac{1}{cos^2u}du\)
\(\left\{{}\begin{matrix}x=1\Rightarrow u=0\\x=2\Rightarrow u=\dfrac{\pi}{4}\end{matrix}\right.\)
\(\Rightarrow I=\int\limits^{\dfrac{\pi}{4}}_0\dfrac{1}{tan^2u+1}.\dfrac{1}{cos^2u}du=\int\limits^{\dfrac{\pi}{4}}_0\dfrac{cos^2u}{cos^2u}du=\int\limits^{\dfrac{\pi}{4}}_0du\)
\(=u|^{\dfrac{\pi}{4}}_0=\dfrac{\pi}{4}\)
c.
\(\int\limits^2_1\dfrac{dx}{\sqrt{4-x^2}}\)
Đặt \(x=2sinu\Rightarrow dx=2cosu.du\)
\(\left\{{}\begin{matrix}x=1\Rightarrow u=\dfrac{\pi}{6}\\x=2\Rightarrow u=\dfrac{\pi}{2}\end{matrix}\right.\)
\(I=\int\limits^{\dfrac{\pi}{2}}_{\dfrac{\pi}{6}}\dfrac{2cosu.du}{\sqrt{4-4sin^2u}}=\int\limits^{\dfrac{\pi}{2}}_{\dfrac{\pi}{6}}\dfrac{2cosu.du}{2cosu}=\int\limits^{\dfrac{\pi}{2}}_{\dfrac{\pi}{6}}du\)
\(=u|^{\dfrac{\pi}{2}}_{\dfrac{\pi}{6}}=\dfrac{\pi}{3}\)
Hãy tính khối lượng thể tích (ở điều kiện tiêu chuẩn),số phân tử sau:
a, 0,02 mol CO2
b,0,75 mol H2S
\(a,m_{CO_2}=0,02.44=0,88(g)\\ V_{CO_2}=0,02.22,4=0,448(l)\\ \text{Số phân tử }CO_2:0,02.6.10^{23}=0,12.10^{23}\\ b,m_{H_2S}=0,75.34=25,5(g)\\ V_{H_2S}=0,75.22,4=16,8(l)\\ \text{Số phân tử }H_2S:0,75.6.10^{23}=4,5.10^{23}\)
Tính diện tích và chu vi các hình được tô màu sau:
a)
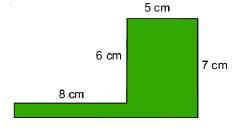
b)
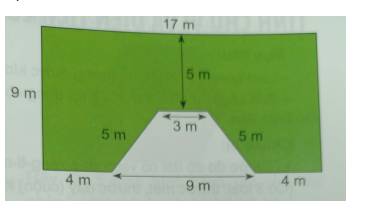
a)

Ta chia hình ban đầu thành hình chữ nhật nhỏ có chiều dài 8 cm và chiều rộng là: 7-6=1cm và hình chữ nhật lớn có chiều dài 7cm và chiều rộng là 5cm.
Diện tích hình chữ nhật nhỏ là \(8.1 = 8\left( {c{m^2}} \right)\).
Diện tích hình chữ nhật lớn là \(5.7 = 35\left( {c{m^2}} \right)\).
Diện tích hình được tô màu là \(8 + 35 = 43\left( {c{m^2}} \right)\).
Chu vi hình được tô màu cũng chính bằng chu vi hình chữ nhật có chiều rộng 7 cm, chiều dài 13 cm và là:
2.(7+13) = 40 (cm)
b)

Diện tích hình chữ nhật lớn là \(17.9 = 153\left( {{m^2}} \right)\)
Hình thang cân có chiều cao là \(9 - 5 = 4\left( m \right)\), đáy bé là 3m, đáy lớn là 9 m.
Diện tích hình thang cân là \(S = \frac{{\left( {3 + 9} \right).4}}{2} = 24\left( {{m^2}} \right)\)
Diện tích hình được tô màu là \(153 - 24 = 129\left( {{m^2}} \right)\).
Chu vi hình được tô màu là:
17+9+4+5+3+5+4+9 = 56 (m)
. Tính số mol nguyên tử hoặc phân tử trong các lượng chất sau:
a) 1,44.1023 phân tử HCl
b) 24.1023 nguyên tử N
a) 1,44.1023 phân tử HCl
n HCl =\(\dfrac{1,44.10^{23}}{6.10^{23}}\)=0,24 mol
b) 24.1023 nguyên tử N
n N=\(\dfrac{24,10^{23}}{6.10^{23}}\)=4 mol
Câu 1. (1,0 đ) Phân tích các đa thức sau thành nhân tử:
a. b.
Câu 2. (2,5 đ) Thực hiện các phép tính sau:
a)
a) ;
b)
Câu 3. (2,5 đ) Cho tam giác ABC vuông tại A (AB < AC) và đường cao AH. Từ H kẻ HE vuông góc với AB, HF vuông góc với AC (E thuộc AB; F thuộc AC).
a) Chứng minh tứ giác AEHF là hình chữ nhật.
b) Vẽ điểm D đối xứng với A qua F. Chứng minh tứ giác DHEF là hình bình hành.
c) Tam giác ABC cần thêm điều kiện gì thì tứ giác AEHF là hình vuông?
Câu 3:
a: Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
Do đó: AEHF là hình chữ nhật
1. Quy đồng mẫu các phân số sau:
a) \(\frac{5}{{12}}\) và \(\frac{7}{{15}}\); b) \(\frac{2}{7};\,\,\frac{4}{9}\) và \(\frac{7}{{12}}\).
2. Thực hiện các phép tính sau:
a) \(\frac{3}{8} + \frac{5}{{24}};\) b) \(\frac{7}{{16}} - \frac{5}{{12}}.\)
1. a) Ta có BCNN(12, 15) = 60 nên ta lấy mẫu chung của hai phân số là 60.
Thừa số phụ:
60:12 =5; 60:15=4
Ta được:
\(\frac{5}{{12}} = \frac{{5.5}}{{12.5}} = \frac{{25}}{{60}}\)
\(\frac{7}{{15}} = \frac{{7.4}}{{15.4}} = \frac{{28}}{{60}}\)
b) Ta có BCNN(7, 9, 12) = 252 nên ta lấy mẫu chung của ba phân số là 252.
Thừa số phụ:
252:7 = 36; 252:9 = 28; 252:12 = 21
Ta được:
\(\frac{2}{7} = \frac{{2.36}}{{7.36}} = \frac{{72}}{{252}}\)
\(\frac{4}{9} = \frac{{4.28}}{{9.28}} = \frac{{112}}{{252}}\)
\(\frac{7}{{12}} = \frac{{7.21}}{{12.21}} = \frac{{147}}{{252}}\)
2. a) Ta có BCNN(8, 24) = 24 nên:
\(\frac{3}{8} + \frac{5}{{24}} = \frac{{3.3}}{{8.3}} + \frac{5}{{24}} = \frac{9}{{24}} + \frac{5}{{24}} = \frac{{14}}{{24}} = \frac{7}{{12}}\)
b) Ta có BCNN(12, 16) = 48 nên:
\(\frac{7}{{16}} - \frac{5}{{12}} = \frac{{7.3}}{{16.3}} - \frac{{5.4}}{{12.4}} = \frac{{21}}{{48}} - \frac{{20}}{{48}} = \frac{1}{{48}}\).
Hãy tra cứu các điển tích, điển cố và phân tích tác dụng của việc sử dụng điển tích, điển cố đó trong các trường hợp sau:
a. Vân Tiên tả đột hữu xông
Khác nào Triệu Tử mở vòng Đương Dương
( Lục Vân Tiên - Nguyễn Đình Chiểu)
b. Công danh nam tử còn Vương nợ
Luống thẹn tai nghe chuyện Vương Hầu
( Tỏ lòng - Phạm Ngũ Lão)
c. Dẽ có Ngu cầm đàn một tiếng
Dân giàu đủ khắp đòi phương
( Cảnh ngày hè - Nguyễn Trãi)
d. Rượu, đến cội cây ta sẽ uống
Nhìn xem phú quý tựa chiêm bao
( Nhàn - Nguyễn Bỉnh Khiêm)
Bài 1. Tính % khối lượng các nguyên tố có trong các phân tử sau:
a) CO; MgCl2; C6H6.
b) FeO; Fe3O4;
c) CuSO4; CaCO3
Làm một cái rồi tương tự nhé
\(a,\%C=\dfrac{12}{44}=27,27\%\\ \%O=100\%-27,27\%=72,73\%\)
\(a,CO\\ \%m_C=\dfrac{M_C}{M_C+M_O}.100\%=\dfrac{12}{12+16}.100\approx42,857\%\\ \Rightarrow\%m_O\approx100\%-42,857\%\approx57,143\%\\ MgCl_2\\ \%m_{Mg}=\dfrac{M_{Mg}}{M_{Mg}+2.M_{Cl}}.100\%=\dfrac{24}{24+2.35,5}.100\approx25,263\%\\ \Rightarrow\%m_{Cl}\approx100\%-25,263\%\approx74,737\%\\ C_6H_6\\ \%m_C=\dfrac{6.M_C}{6.M_C+6.M_H}.100\%=\dfrac{6.12}{6.12+6.1}.100\approx92,308\%\\ \Rightarrow\%m_H\approx100\%-92,308\%\approx7,692\%\)
\(b,FeO\\ \%m_{Fe}=\dfrac{M_{Fe}}{M_{Fe}+M_O}.100\%=\dfrac{56}{56+16}.100\approx77,778\%\\ \Rightarrow\%m_O\approx100\%-77,778\%=22,222\%\\ Fe_3O_4\\ \%m_{Fe}=\dfrac{3.M_{Fe}}{3.M_{Fe}+4.M_O}.100\%=\dfrac{3.56}{3.56+4.16}.100\approx72,414\%\\ \Rightarrow\%m_O\approx100\%-72,414\%\approx27,586\%\)
\(c,CuSO_4\\ \%m_{Cu}=\dfrac{M_{Cu}}{M_{Cu}+M_S+4.M_O}.100\%=\dfrac{64}{64+32+4.16}.100=40\%\\ \%m_S=\dfrac{M_S}{M_{Cu}+M_S+4.M_O}.100\%=\dfrac{32}{64+32+4.16}.100=20\%\\ \Rightarrow\%m_O=100\%-\left(\%m_{Cu}+\%m_S\right)=100\%-\left(40\%+20\%\right)=40\%\\ CaCO_3\\ \%m_{Ca}=\dfrac{M_{Ca}}{M_{Ca}+M_C+3.M_O}.100\%=\dfrac{40}{40+12+3.16}.100=40\%\\ \%m_C=\dfrac{M_C}{M_{Ca}+M_C+3.M_O}.100\%=\dfrac{12}{40+12+3.16}.100=12\%\\ \Rightarrow\text{ }\%m_O=100\%-\left(40\%+12\%\right)=48\%\)