Giúp mình với. Mình đang gấp . Mình cảm ơn nhiều

Những câu hỏi liên quan
giúp mình với mình đang cần gấp. Cảm ơn nhiều
giúp mình nhanh với ạ, mình đang cần gấp, mình cảm ơn nhiều 
Gọi s là diện tích đáy của thanh.
Đổi 10cm = 0,1m; 3cm = 0,03m
Thể tích của thanh là:
V=0,1⋅s=0,1s
Thể tích phần nổi của thanh là:
Vnổi=0,03⋅s=0,03s
Thể tích phần chìm của thanh là:
Vchìm=0,1s − 0,03s=0,07s
Lực đẩy Ác - si - mét tác dụng lên thanh là:
FA = 0,07s⋅10000 = 700s
Do vật nổi ⇒FA=P⇒FA=P
Trọng lượng của thanh là: P=700s
⇒ Khối lượng của thanh là:
m = 700s:10=70
Khối lượng riêng của thanh là:
D = 70s:0,1s = 700kg/m3
Đúng 1
Bình luận (6)
Gọi S là diện tích của đáy thanh đồng chất
Đổi: \(10cm=0,1m;3cm=0,03cm\)
Thể tích của thanh đồng là: \(V_{tổng}=S.0,1=0,1S\left(m^3\right)\)
Thể tích phần nổi của thanh đồng là: \(V_{nổi}=S.0,03=0,03S\left(m^3\right)\)
Thể tích phần chìm của thanh là: \(V_{chìm}=V_{tổng}-V_{nổi}=0,1S-0,03S=0,07S\left(m^3\right)\)
Lực đẩy Achimedes tác dụng lên thanh đồng là: \(F_A=d_{nước}.V_{chìm}=10000.0,07S=700S\)
Do vật ko nổi hẳn cũng ko chìm hẳn nên: \(F_A=P=700S\)
Khối lượng của thanh đồng là: \(m=\dfrac{P}{10}=\dfrac{700S}{10}=70S\left(kg\right)\)
Khối lượng riêng của thanh đồng là: \(d_{thanh.đồng}=\dfrac{m}{V_{tổng}}=\dfrac{70S}{0,1S}=700\left(\dfrac{kg}{m^3}\right)\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Giúp mình với ạ, mình đang cần gấp, cảm ơn nhiều


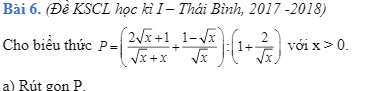
giải giúp mình câu này với mình đang cần gấp, mình cảm ơn rất nhiều
\(P=\dfrac{2\sqrt{x}+1+\left(1-\sqrt{x}\right)\left(1+\sqrt{x}\right)}{\sqrt{x}\left(\sqrt{x}+1\right)}:\dfrac{\sqrt{x}+2}{\sqrt{x}}\)
\(=\dfrac{2\sqrt{x}+1+1-x}{\sqrt{x}\left(\sqrt{x}+1\right)}.\dfrac{\sqrt{x}}{\sqrt{x}+2}=\dfrac{-x+2\sqrt{x}+2}{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)}=\dfrac{-x+2\sqrt{x}+2}{x+3\sqrt{x}+2}\)
Đúng 1
Bình luận (1)
Mình đang cần gấp. Mọi người giúp mình với ạ! Mình cảm ơn nhiều! 😊
Giúp mình với ạ, mình đang cần gấp Cảm ơn nhiều ❤
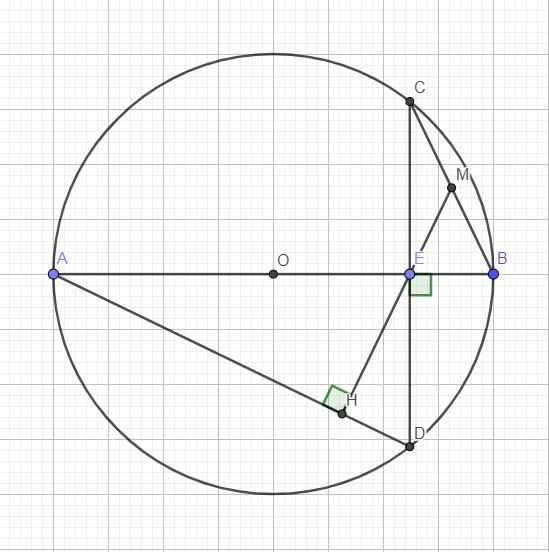
Tứ giác ACBD nội tiếp \(\Rightarrow\widehat{ADC}=\widehat{ABC}\) (cùng chắn AC) (1)
Lại có \(\widehat{ADC}+\widehat{DEH}=90^0\) (tam giác DEH vuông tại H theo gt) (2)
Gọi M là trung điểm BC, nối EM
Trong tam giác vuông BCE, EM là trung tuyến ứng với cạnh huyền
\(\Rightarrow EM=\dfrac{1}{2}BC=BM\Rightarrow\Delta BEM\) cân tại M
\(\Rightarrow\widehat{ABC}=\widehat{MEB}\) (3)
\(\left(1\right);\left(2\right);\left(3\right)\Rightarrow\widehat{DEH}+\widehat{MEB}=90^0\)
\(\Rightarrow\widehat{DEH}+\widehat{MEB}+\widehat{DEB}=90^0+90^0=180^0\)
\(\Rightarrow M;E;H\) thẳng hàng hay HE đi qua trung điểm M của BC
Đúng 2
Bình luận (0)
Giúp mình với, mình đang cần gấp. Cảm ơn các bạn nhiều
b4
1, (x-y)3
3, [(x-y)(x+y)] - 4(x-y)
= (x-y) [(x+y) - 4]
Đúng 0
Bình luận (0)
Bài 4:
d: Ta có: \(x^2-y^2-2x-2y\)
\(=\left(x-y\right)\left(x+y\right)-2\left(x+y\right)\)
\(=\left(x+y\right)\left(x-y-2\right)\)
e: Ta có: \(x^3-y^3-3x+3y\)
\(=\left(x-y\right)\left(x^2+xy+y^2\right)-3\left(x-y\right)\)
\(=\left(x-y\right)\left(x^2+xy+y^2-3\right)\)
Đúng 0
Bình luận (0)
 Mn giúp mình bài 3 với ạ. Mình đang cần gấp lắm. Mình cảm ơn nhiều !
Mn giúp mình bài 3 với ạ. Mình đang cần gấp lắm. Mình cảm ơn nhiều !
Giúp mình với mình đang cần gấp quá. Cảm ơn các bạn nhiều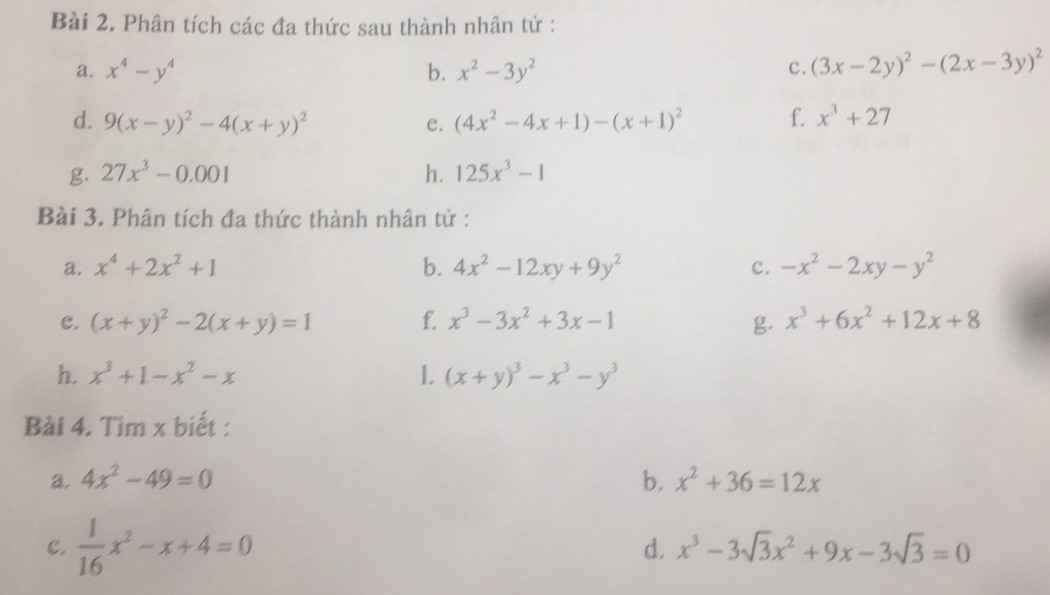
2.
\(a,x^4-y^4=\left(x^2-y^2\right)\left(x^2+y^2\right)=\left(x-y\right)\left(x+y\right)\left(x^2+y^2\right)\)
\(b,x^2-3y^2=\left(x-y\sqrt{3}\right)\left(x+y\sqrt{3}\right)\)
\(c,\left(3x-2y\right)^2-\left(2x-3y\right)^2\\ =\left(3x-2y-2x+3y\right)\left(3x-2y+2x-3y\right)\\ =\left(x+y\right)\left(5x-5y\right)=5\left(x-y\right)\left(x+y\right)\)
\(d,9\left(x-y\right)^2-4\left(x+y\right)^2\\ =\left[3\left(x-y\right)-2\left(x+y\right)\right]\left[3\left(x-y\right)+2\left(x+y\right)\right]\\ =\left(3x-3y-2x-2y\right)\left(3x-3y+2x+2y\right)\\ =\left(x-5y\right)\left(5x-y\right)\)
\(e,\left(4x^2-4x+1\right)-\left(x+1\right)^2\\ =\left(2x-1\right)^2-\left(x+1\right)^2\\ =\left(2x-1-x-1\right)\left(2x-1+x+1\right)\\ =3x\left(x-2\right)\)
\(f,x^3+27=\left(x+3\right)\left(x^2+3x+9\right)\)
\(g,27x^3-0,001=\left(3x-0,1\right)\left(9x^2+0,027x+0,01\right)\)
\(h,125x^3-1=\left(5x-1\right)\left(25x^2+5x+1\right)\)
Đúng 3
Bình luận (0)
Bài 3 :
a) \(x^4+2x^2+1=\left(x^2+1\right)^2\)
b) \(4x^2-12xy+9y^2=\left(2x-3y\right)^2\)
c) \(-x^2-2xy-y^2=-\left(x+y\right)^2\)
e) \(\left(x+y\right)^2-2\left(x+y\right)+1=\left(x+y-1\right)^2\)
f) \(x^3-3x^2+3x-1=\left(x-1\right)^3\)
g) \(x^3+6x^2+12x+8=\left(x+2\right)^3\)
h) \(x^3+1-x^2-x=\left(x+1\right)\left(x^2-x+1\right)-x\left(x+1\right)=\left(x+1\right)\left(x^2-2x+1\right)=\left(x+1\right)\left(x-1\right)^2\)
l) \(\left(x+y\right)^2-x^3-y^3=\left(x+y\right)^3-\left(x+y\right)\left(x^2-xy+y^2\right)=\left(x+y\right)\left(x^2+2xy+y^2-x^2+xy-y^2\right)=3xy\left(x+y\right)\)
Đúng 0
Bình luận (0)
Bài 4:
a: Ta có: \(4x^2-49=0\)
\(\Leftrightarrow\left(2x-7\right)\left(2x+7\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{7}{2}\\x=-\dfrac{7}{2}\end{matrix}\right.\)
b: Ta có: \(x^2+36=12x\)
\(\Leftrightarrow x^2-12x+36=0\)
\(\Leftrightarrow\left(x-6\right)^2=0\)
\(\Leftrightarrow x-6=0\)
hay x=6
c: Ta có: \(\dfrac{1}{16}x^2-x+4=0\)
\(\Leftrightarrow\left(\dfrac{1}{4}x-2\right)^2=0\)
\(\Leftrightarrow x\cdot\dfrac{1}{4}-2=0\)
\(\Leftrightarrow x\cdot\dfrac{1}{4}=2\)
hay x=8
d: Ta có: \(x^3-3\cdot x^2\cdot\sqrt{3}+9x-3\sqrt{3}=0\)
\(\Leftrightarrow\left(x-\sqrt{3}\right)^3=0\)
\(\Leftrightarrow x-\sqrt{3}=0\)
hay \(x=\sqrt{3}\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời