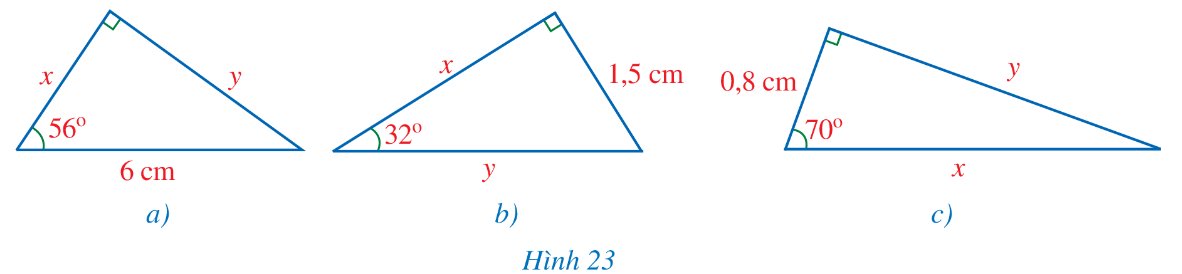
Tìm x, y trong mỗi hình 23a, 23b, 23c (làm tròn kết quả đến hàng phần mười của centimét).
1.Làm tròn số 92,117 đến hàng phần mười được kết quả là
2.Làm tròn số -845,654 đến hàng phần mười (đến chữ số thập phân thứ nhất) được kết quả là:
3.Làm tròn số 82,572 đến hàng phần mười được kết quả là:
4.Làm tròn số 82,572 đến hàng phần mười được kết quả là:
5.Làm tròn số -72,882 đến chữ số thập phân thứ nhất được kết quả là
1.Làm tròn số 92,117 đến hàng phần mười được kết quả là:92,1
2.Làm tròn số -845,654 đến hàng phần mười (đến chữ số thập phân thứ nhất) được kết quả là:-845,7
3.Làm tròn số 82,572 đến hàng phần mười được kết quả là:82,6
4.Làm tròn số 82,572 đến hàng phần mười được kết quả là:82,6
5.Làm tròn số -72,882 đến chữ số thập phân thứ nhất được kết quả là:-72,9
\(92,117\approx92,12\\ -845,654\approx-845,65\approx-845,7\\ 82,572\approx82,57\\ 82,572\approx82,57\\ -72,882\approx-72,9\)
Làm tròn số 92,117 đến hàng phần mười được kết quả là:
Làm tròn số -845,654 đến hàng phần mười (đến chữ số thập phân thứ nhất) được kết quả là:
Làm tròn số 82,572 đến hàng phần mười được kết quả :
Làm tròn số -72,882 đến chữ số thập phân thứ nhất được kết quả là
Làm tròn số -7671,08 đến hàng chục được kết quả là
Làm tròn số 86427 đến hàng trăm được kết quả là:
Làm tròn số 28,1 đến hàng đơn vị được kết quả là:
Làm tròn số -28,7 đến hàng đơn vị được kết quả là
Làm tròn số 128,5 đến hàng chục được kết quả là:
Làm tròn số 28,23 đến hàng đơn vị được kết quả là:
Làm tròn số 5960,12 đến hàng trăm được kết quả là
Làm tròn số -2367,785 đến chữ số thập phân thứ hai được kết quả là:
Làm tròn số 327,7892 đến chữ số thập phân thứ hai được kết quả là:
Làm tròn số -29670 đến hàng nghìn được kết quả là:
Làm tròn số 7476,5 đến hàng đơn vị được kết quả là
Làm tròn số 4568,12 đến hàng trăm được kết quả là:
Làm tròn số -28,39 đến hàng phần mười được kết quả là:
Làm tròn số -67,193 đến chữ số thập phân thứ hai được kết quả là:
Làm tròn số -18,119 đến chữ số thập phân thứ hai được kết quả là
Làm tròn số -15427,99 đến hàng trăm được kết quả là:
Trong bài toán ở phần mở đầu, độ cao y (m) của một điểm thuộc vòng cung thành cầu cảng Sydney đạt giá trị lớn nhất là bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?
- Cách 1:
Hàm số biểu diễn đồ thị \(y = - 0,00188{\left( {x - 251,5} \right)^2} + 118\)
\(\begin{array}{l}{\left( {x - 251,5} \right)^2} \ge 0\\ \Leftrightarrow - 0,00188{\left( {x - 251,5} \right)^2} \le 0\\ \Leftrightarrow - 0,00188{\left( {x - 251,5} \right)^2} + 118 \le 118\end{array}\)
Khi đó độ cao y (m) của một điểm thuộc vòng cung thành cầu cảng Sydney đạt giá trị lớn nhất là \(y = 118\left( m \right)\)
- Cách 2:
Ta có phương trình thành cầu: \(y = – 0,00188(x – 251,5)^2 + 118\)
\( \Leftrightarrow y = – 0,00188x^2 + 0,94564x – 0,91423\), là hàm số bậc hai.
Vì a = – 0,00188 < 0 nên đồ thị hàm số trên có bề lõm hướng xuống dưới hay đỉnh I của đồ thị là điểm cao nhất, vậy giá trị lớn nhất cần tìm chính là tung độ của đỉnh I.
Ta có: \(b = 0,94564, c = – 0,91423\)
\( x_I = \frac{-b}{2a}= \frac{-0,94564}{2. (-0,00188)}=251,5 \Rightarrow y_I = – 0,00188(x_I – 251,5)^2 + 118 =118.\)
Vậy độ cao lớn nhất cần tìm là 118 m.
Dùng máy tính cầm tay để A) tính độ dài cạnh của một miếng đất hình vuông có S=12 996m² B) Tính bán kính của 1 hình tròn có S=100 cm²(làm tròn kết quả đến hàng phần mười)
Lời giải:
a. Ta có: $12996=114\times 114$ nên độ dài cạnh miếng đất là $114$ (m)
b. $3,14 R^2=100$
$R^2=100:3,14$=31,84$
$R=\sqrt{31,84}=5,6$ (cm)
mình nhầm bạn ơi,phải là 3,142 mới đúng nhé:((
Hỏi kết quả làm tròn số 32,1534 đến hàng phần mười?
A. 32,2
B. 32,15
C. 30
D. 32
Câu 9: Chia đều 1 thanh gỗ dài 8,32m thành 4 đoạn thẳng bằng nhau. Tính độ dài mỗi đoạn gỗ ( Làm tròn kết quả đến hàng phần mười)
A.2m B.2,18m C.2,1m D.2,08m
Trong câu a, nếu viết kết quả làm tròn là 24 thì có đúng không?
Câu a: Làm tròn số 24,037 tới hàng phần mười.
Viết kết quả làm tròn là 24 thì vẫn đúng vì \(24,0 = \dfrac{{240}}{{10}} = \dfrac{{24}}{1} = 24\)
Một bánh xe hình tròn có đường kính là 700 mm chuyển động trên một đường thẳng từ điểm A đến điểm B sau 875 vòng. Quãng đường AB dài khoảng bao nhiêu ki-lô-mét (làm tròn kết quả đến hàng phần mười và lấy π = 3,14)?
Cho tam giác ABC có \(AB = 3,5;\;AC = 7,5;\;\widehat A = {135^o}.\) Tính độ dài cạnh BC và bán kính R của đường tròn ngoại tiếp tam giác (làm tròn kết quả đến hàng phần mười).
Áp dụng định lí cosin trong tam giác ABC ta có:
\(B{C^2} = A{C^2} + A{B^2} - 2AC.AB.\cos A\)
\(\begin{array}{l} \Leftrightarrow B{C^2} = 7,{5^2} + 3,{5^2} - 2.7,5.3,5.\cos {135^o}\\ \Leftrightarrow B{C^2} \approx 105,6\\ \Leftrightarrow BC \approx 10,3\end{array}\)
Áp dụng định lí sin trong tam giác ABC ta có: \(\frac{{BC}}{{\sin A}} = 2R\)
\( \Rightarrow R = \frac{{BC}}{{2.\sin A}} = \frac{{10,3}}{{2.\sin {{135}^o}}} \approx 7,3\)