21+3x-2=48
hẹp mi
 Hẹp mi hẹp mi pờ li😩
Hẹp mi hẹp mi pờ li😩
I
1. A ronot is a speacial kind of machine.
2. No, it isn't
3. Worker Robots can help make cars, and explore volcanoes, ...
4. No, it wasn't
II
1. No, there aren't. There are 2 kinds of sports.
2. Team sports require 2 separate teams.
3. Because they want to get the best score.
4. Yes, they are.
Bài 2.Tìm x
a,(x-15)+124=200
b,3x-21=3^6:3^4
c,x-48:16==21
a) x-15+124=200
x-15=200-124
x-15=76
x=76+15
x=91
Vậy x=91.
b) 3x-21=36:34
3x-21=32
3x-21=9
3x=9+21
3x=30
x=30:3
x=10
Vậy x=10.
c) x-48:16=21
x-3=21
x=21+3
x=24
Vậy x=24.
a,(x-15)+124=200
x - 15 = 200 - 124
x - 15 = 76
x = 76 + 15
x = 91.
Vậy x = 91.
b,3x-21=36:34
3x - 21 = 32
3x - 21 = 9
3x = 9 + 21
3x = 30
x = 30 : 3
x = 10.
Vậy x = 10.
c,x-48:16=21
x - 3 = 21
x = 21 + 3
x = 24.
Vậy x = 24
# HOK TỐT #
hẹp mi
hẹp mi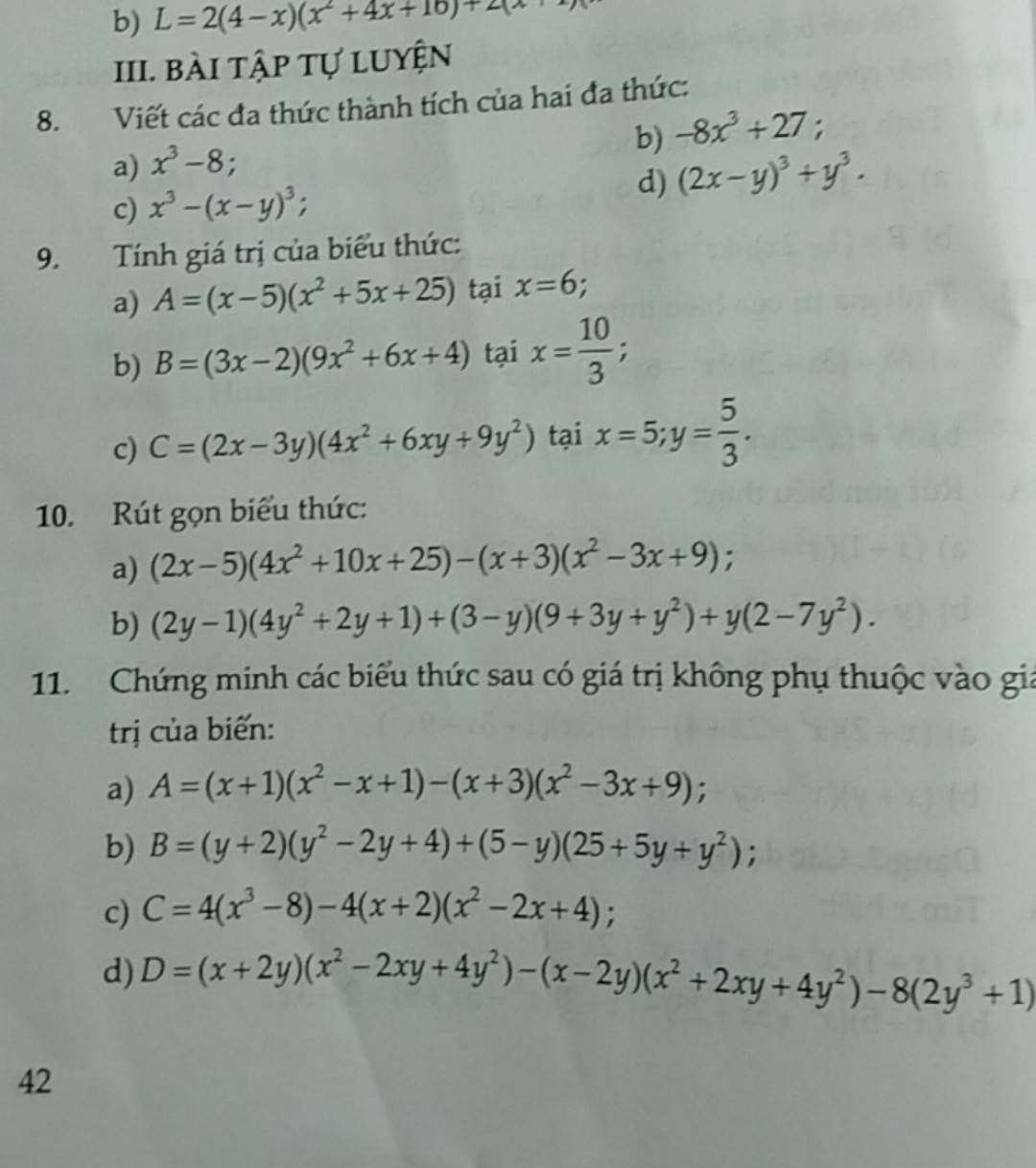
1;Tính
235-288:[4×(48-72)]
2;Tìmx
2x+12-3x=-21
\(2x+12-3x=-21\)
\(x.\left(2+12-3\right)=-21\)
\(x.11=-21\)
\(x=-\frac{21}{11}\)
\(235-288:\left[4\times\left(48-72\right)\right]\)
\(=235-288:4\times\left(48-72\right)\)
\(=235-72\times\left(-24\right)\)
\(=235-\left(-1728\right)\)
\(=235+1728\)
\(=1963\)
Tam giác ABC. BM là phân giác góc B. CN là phân giác góc C. BN+CM=BC Tính góc A Huuu hẹp mi hẹp mi! Giúp t vs akk, t ngu hình r😮💨🥲
Gọi D là giao điểm BM và CN.
Trên cạnh BC lấy điểm E sao cho \(BE=BN\)
Khi đó \(CE=BC-BE=BN+CM-BE=CM\)
Xét hai tam giác BDE và BDN có:
\(\left\{{}\begin{matrix}BE=BN\\\widehat{DBE}=\widehat{DBN}\left(\text{BM là phân giác}\right)\\BD\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta BDE=\Delta BDN\left(c.g.c\right)\)
\(\Rightarrow\widehat{BDE}=\widehat{BDN}\)
Hoàn toàn tương tự, ta cũng có \(\Delta CDE=\Delta CDM\left(c.g.c\right)\Rightarrow\widehat{CDE}=\widehat{CDM}\)
Mà \(\widehat{BDN}=\widehat{CDM}\) (đối đỉnh) \(\Rightarrow\widehat{BDN}=\widehat{BDE}=\widehat{CDM}=\widehat{CDE}\)
Mà \(\widehat{BDE}+\widehat{CDE}+\widehat{CDM}=180^0\)
\(\Rightarrow3\widehat{BDE}=180^0\Rightarrow\widehat{BDE}=60^0\)
\(\Rightarrow\widehat{CDE}=60^0\)
\(\Rightarrow\widehat{BDC}=\widehat{BDE}+\widehat{CDE}=120^0\)
Theo tính chất tổng 3 góc tổng tam giác:
\(\widehat{BDC}+\widehat{DBC}+\widehat{DCB}=180^0\)
\(\Rightarrow120^0+\dfrac{1}{2}\widehat{B}+\dfrac{1}{2}\widehat{C}=180^0\)
\(\Rightarrow\widehat{B}+\widehat{C}=120^0\)
Do tổng 3 góc trong tam giác ABC bằng 180 độ
\(\Rightarrow\widehat{A}+\widehat{B}+\widehat{C}=180^0\)
\(\Rightarrow\widehat{A}+120^0=180^0\)
\(\Rightarrow A=60^0\)

hẹp mi với ạ
Bài 5:
a)
\(x^4+x^3+x+1\\ =x^3\left(x+1\right)+\left(x+1\right)\\ =\left(x^3+1\right)\left(x+1\right)\)
b)
\(x^4-x^3-x+1\\ =x^3\left(x-1\right)-\left(x-1\right)\\ =\left(x^3-1\right)\left(x-1\right)\\ =\left(x-1\right)\left(x^2+x+1\right)\left(x-1\right)\)
c)
\(3x^2-12y^2\\ =\left(\sqrt{3}x\right)^2-\left(\sqrt{12}y\right)^2\\ =\left(\sqrt{3}x-\sqrt{12}y\right)\left(\sqrt{3}x+\sqrt{12}y\right)\\ =\sqrt{3}\left(x-\sqrt{4}y\right).\sqrt{3}\left(x+\sqrt{4}y\right)\\ =3\left(x-\sqrt{4}y\right)\left(x+\sqrt{4}y\right)\)
7:
a: (2x-1)^2-25=0
=>(2x-1)^2=25
=>2x-1=-5 hoặc 2x-1=5
=>2x=6 hoặc 2x=-4
=>x=-2 hoặc x=3
b: 8x^3-50x=0
=>4x^3-25x=0
=>x(4x^2-25)=0
=>x(2x-5)(2x+5)=0
=>x=0 hoặc 2x-5=0 hoặc 2x+5=0
=>x=0;x=5/2;x=-5/2
c: 3x(x-1)+(x-1)=0
=>(x-1)(3x+1)=0
=>x=1 hoặc x=-1/3
d: =>2(x+3)-x(x+3)=0
=>(x+3)(2-x)=0
=>x=-3 hoặc x=2
e: Thiếu vế phải rồi bạn
f: x^3+27+(x+3)(x-9)=0
=>(x+3)(x^2-3x+9)+(x+3)(x-9)=0
=>(x+3)(x^2-3x+9+x-9)=0
=>(x+3)(x^2-2x)=0
=>x(x-2)(x+3)=0
=>\(x\in\left\{0;2;-3\right\}\)
Bài 6:
\(B=\left(x-1\right)x^2-4x\left(x-1\right)+4\left(x-1\right)\\ =\left(x-1\right)\left(x^2-4x+4\right)\\ =\left(x-1\right)\left(x-2\right)^2\)
Thay x = 3 vào biểu thức B, ta có:
\(B=\left(3-1\right)\left(3-2\right)^2=2\cdot1^2=2\)
Hẹp mi mụi ngừi uiiiii
Lúc đầu, người bán hàng có: \(50\div\dfrac{2}{5}+1=126\) (trái)
Đ/s:..
Lúc đầu, người bán hàng có: \(\left(50+1\right)\div\left(1-\dfrac{2}{5}\right)=85\)
1. |48 - 3x| = 0
2. |-x - 7|= 24
3. |4 - x| = 21
4. |x + 8| + 12 = 0
5. 6 - |x| = 2
Giải:
a) \(\left|48-3x\right|=0\)
\(\Leftrightarrow48-3x=0\)
\(\Leftrightarrow3x=48\)
\(\Leftrightarrow x=\dfrac{48}{3}=16\)
Vậy x = 16.
b) \(\left|-x-7\right|=24\)
\(\Leftrightarrow\left[{}\begin{matrix}-x-7=24\\-x-7=-24\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}-x=31\\-x=-17\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-31\\x=17\end{matrix}\right.\)
Vậy \(x=-31\) hoặc \(x=17\).
c) \(\left|4-x\right|=21\)
\(\Leftrightarrow\left[{}\begin{matrix}4-x=21\\4-x=-21\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-17\\x=25\end{matrix}\right.\)
Vậy \(x=-17\) hoặc \(x=25\).
d) \(\left|x+8\right|+12=0\)
\(\Leftrightarrow\left|x+8\right|=-12\)
\(\Leftrightarrow\left[{}\begin{matrix}x+8=-12\\x+8=-\left(-12\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-20\\x=4\end{matrix}\right.\)
Vậy \(x=-20\) hoặc \(x=4\).
e) \(6-\left|x\right|=2\)
\(\Leftrightarrow\left|x\right|=6-2=4\)
\(\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-4\end{matrix}\right.\)
Vậy \(x=4\) hoặc \(x=-4\).
Chúc bạn học tốt!
1. |48 - 3x| = 0.
\(\Leftrightarrow\) 48 - 3x = 0.
\(\Leftrightarrow\) 3x = 48.
\(\Leftrightarrow\) x = \(\dfrac{48}{3}=16.\)
Vậy x = 16.
2. |-x - 7| = 24.
\(\Leftrightarrow\left[{}\begin{matrix}-x-7=24.\\-x-7=-24.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}-x=31.\\-x=-17.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-31.\\x=17.\end{matrix}\right.\)
Vậy \(\left[{}\begin{matrix}x=-31.\\x=17.\end{matrix}\right.\)
3. |4 - x| = 21.
\(\Leftrightarrow\left[{}\begin{matrix}4-x=21.\\4-x=-21.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-17.\\x=25.\end{matrix}\right.\)
Vậy \(\left[{}\begin{matrix}x=-17.\\x=25.\end{matrix}\right.\)
4. |x + 8| + 12 = 0.
|x + 8| = 0 - 12.
|x + 8| = -12.
\(\Leftrightarrow\left[{}\begin{matrix}x+8=-12.\\x+8=-\left(-12\right).\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x+8=-12.\\x+8=12.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-20.\\x=4.\end{matrix}\right.\)
Vậy \(\left[{}\begin{matrix}x=-20.\\x=4.\end{matrix}\right.\)
5. 6 - |x| = 2.
|x| = 6 - 2.
|x| = 4.
\(\Leftrightarrow\left[{}\begin{matrix}x=4.\\x=-4.\end{matrix}\right.\)
Vậy \(\left[{}\begin{matrix}x=4.\\x=-4.\end{matrix}\right.\)
1. Ta có 2 trường hợp:
TH1: 48-3x=0 <=> 3x=48 <=> x=16
TH2:-48-3x=0