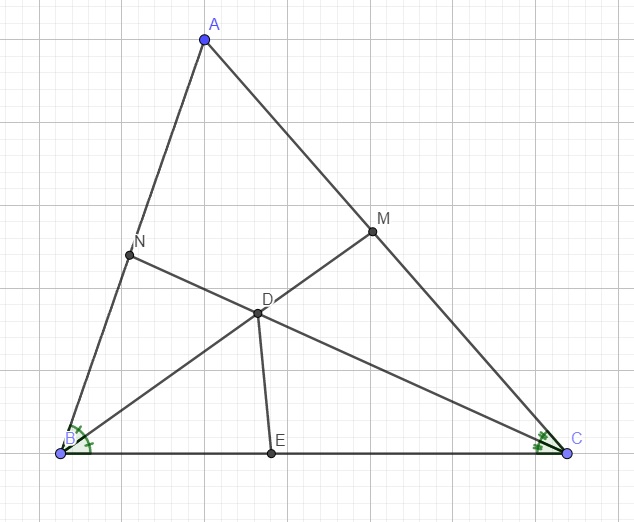
Gọi D là giao điểm BM và CN.
Trên cạnh BC lấy điểm E sao cho \(BE=BN\)
Khi đó \(CE=BC-BE=BN+CM-BE=CM\)
Xét hai tam giác BDE và BDN có:
\(\left\{{}\begin{matrix}BE=BN\\\widehat{DBE}=\widehat{DBN}\left(\text{BM là phân giác}\right)\\BD\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta BDE=\Delta BDN\left(c.g.c\right)\)
\(\Rightarrow\widehat{BDE}=\widehat{BDN}\)
Hoàn toàn tương tự, ta cũng có \(\Delta CDE=\Delta CDM\left(c.g.c\right)\Rightarrow\widehat{CDE}=\widehat{CDM}\)
Mà \(\widehat{BDN}=\widehat{CDM}\) (đối đỉnh) \(\Rightarrow\widehat{BDN}=\widehat{BDE}=\widehat{CDM}=\widehat{CDE}\)
Mà \(\widehat{BDE}+\widehat{CDE}+\widehat{CDM}=180^0\)
\(\Rightarrow3\widehat{BDE}=180^0\Rightarrow\widehat{BDE}=60^0\)
\(\Rightarrow\widehat{CDE}=60^0\)
\(\Rightarrow\widehat{BDC}=\widehat{BDE}+\widehat{CDE}=120^0\)
Theo tính chất tổng 3 góc tổng tam giác:
\(\widehat{BDC}+\widehat{DBC}+\widehat{DCB}=180^0\)
\(\Rightarrow120^0+\dfrac{1}{2}\widehat{B}+\dfrac{1}{2}\widehat{C}=180^0\)
\(\Rightarrow\widehat{B}+\widehat{C}=120^0\)
Do tổng 3 góc trong tam giác ABC bằng 180 độ
\(\Rightarrow\widehat{A}+\widehat{B}+\widehat{C}=180^0\)
\(\Rightarrow\widehat{A}+120^0=180^0\)
\(\Rightarrow A=60^0\)