Câu 1: Tìm x để biểu thức sau có nghĩa:
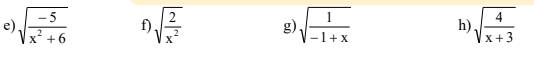
Tìm x để các biểu thức sau có nghĩa và rút gọn các biểu thức sau: a) x-√x /√x-1 - x-1/√x+1
\(\dfrac{x-\sqrt{x}}{\sqrt{x}-1}-\dfrac{x-1}{\sqrt{x}+1}\);\(ĐK:x\ge0;x\ne1\)
\(\Leftrightarrow\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\sqrt{x}-1}-\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}+1}\)
\(\Leftrightarrow\sqrt{x}-\left(\sqrt{x}-1\right)\)
\(\Leftrightarrow\sqrt{x}-\sqrt{x}+1\)
\(\Leftrightarrow1\)
a: \(=\sqrt{x}\cdot\dfrac{\left(\sqrt{x}-1\right)}{\sqrt{x}-1}-\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}+1}\)
\(=\sqrt{x}-\sqrt{x}+1=1\)
Câu 1 a) Tìm câu bậc hai của mỗi số sau : 81; 9 trên 16 b) Tìm x để biểu thức sau có nghĩa : 3 trên căn 2-7x Câu 2 b) (2√3-3√2)^2 +2√6 +3√24 Câu 3 b) Giải Phương Trình : √27x-18-6=√3x-2 Câu6 a) với a là góc nhọn, hãy rút biểu thức: sin^6 alpha + cos^6 alpha +3sin^2 alpha × cos^2 alpha Câu 8: từ đỉnh một tòa nhà cao 54m, người tra nhìn thấy 1 ôtô đang đỗ dưới 1 góc nghiêng xuống là 40°. Hỏi ôtô đang đỗ cách tòa nhà đó khoảng bao nhiêu mét?
giúp tôi giải câu này với :
a, tìm x=? để biểu thức sau có nghĩa A=1/x-1 +căn -2x+3
b, rút gọn biểu thức B=căn75 + căn 48 -1/2căn 300
c,giải phương trình : 4căn2 x^2 -6x-căn2=0
Tìm điều kiện của x để biểu thức sau đây có nghĩa: \(\sqrt{x^2-x+1}\)
\(\sqrt{x^2-x+1}\) có nghĩa khi \(x^2-x+1\ge0\)
Ta có \(x^2-x+1=\left(x^2-x+\dfrac{1}{4}\right)+\dfrac{3}{4}=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\)
Với mọi x, ta có \(\left(x-\dfrac{1}{2}\right)^2\ge0\)
\(\Rightarrow\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\) (vì 3/4 > 0)
Do đó \(x^2-x+1>0\) với mọi x
Vậy với bất cứ giá trị nào của x thì căn thức trên xác định.
ĐKXĐ: `x\inRR`
Vì `x^2-x+1=(x^2-x+1/4)+3/4=(x-1/2)^2+3/4>0AAx`
Tìm gtri của x để biểu thức sau có nghĩa: A = \(\sqrt{1-4x}\)
\(A=\sqrt{1-4x}\)
A có nghĩa khi:
\(1-4x\ge0\)
\(\Leftrightarrow4x\le1\)
\(\Leftrightarrow x\le\dfrac{1}{4}\)
Vậy A có nghĩa khi \(x\le\dfrac{1}{4}\)
ĐKXĐ: 1-4x>=0
=>4x<=1
=>x<=1/4
Tìm điều kiện để biểu thức sau có nghĩa:
\(\dfrac{1}{2}\sqrt{x+3}-x\sqrt{1-x}\)
ĐK:\(\left\{{}\begin{matrix}x+3\ge0\\1-x\ge0\end{matrix}\right.\)\(\Leftrightarrow-3\le x\le1\)
Để biểu thức có nghĩa thì \(\left\{{}\begin{matrix}x+3>0\\1-x>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>-3\\x< 1\end{matrix}\right.\Leftrightarrow-3< x< 1\)
Biểu thức trên có nghĩa khi \(\left\{{}\begin{matrix}x+3\ge0\\1-x\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ge-3\\x\le1\end{matrix}\right.\)
tìm x để biểu thức sau có nghĩa:
\(\dfrac{x-2\sqrt{x+5}}{\sqrt{2x^2+1}}\)
\(\dfrac{x-2\sqrt{x+5}}{\sqrt{2x^2+1}}\) có nghĩa khi
\(\left\{{}\begin{matrix}x+5\ge0\\2x^2+1>0\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x\ge-5\\2x^2+1>0\forall x\in R\end{matrix}\right.\\ \Rightarrow x\ge-5\)
Tìm điều kiện của x để các biểu thức sau có nghĩa
\(\sqrt{\dfrac{1}{x^2-2x+1}}\)
\(\sqrt{\dfrac{1}{x^2-2x+1}}=\sqrt{\dfrac{1}{\left(x-1\right)^2}}=\dfrac{1}{\left|x-1\right|}\)
\(\Rightarrow\) Biểu thức xác định khi \(x-1\ne0\Leftrightarrow x\ne1\).
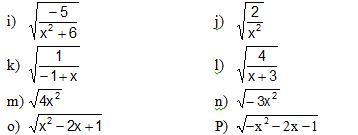 Tìm x để biểu thức sau có nghĩa
Tìm x để biểu thức sau có nghĩa
l, \(x+3>0\Leftrightarrow x>-3\)
m, \(4x^2\ge0\forall x\Rightarrow\) biểu thức xác định với mọi x.
n, \(-3x^2\ge0\Leftrightarrow x=0\)
o, \(x^2-2x+1=\left(x-1\right)^2\ge0\forall x\Rightarrow\) biểu thức xác định với mọi x.
p, \(-x^2-2x-1=-\left(x+1\right)^2\le0\)
Biểu thức xác định khi \(x+1=0\Leftrightarrow x=-1\)
i: ĐKXĐ: \(x\in\varnothing\)
j: ĐKXĐ: \(x\ne0\)
k: ĐKXĐ: x>1