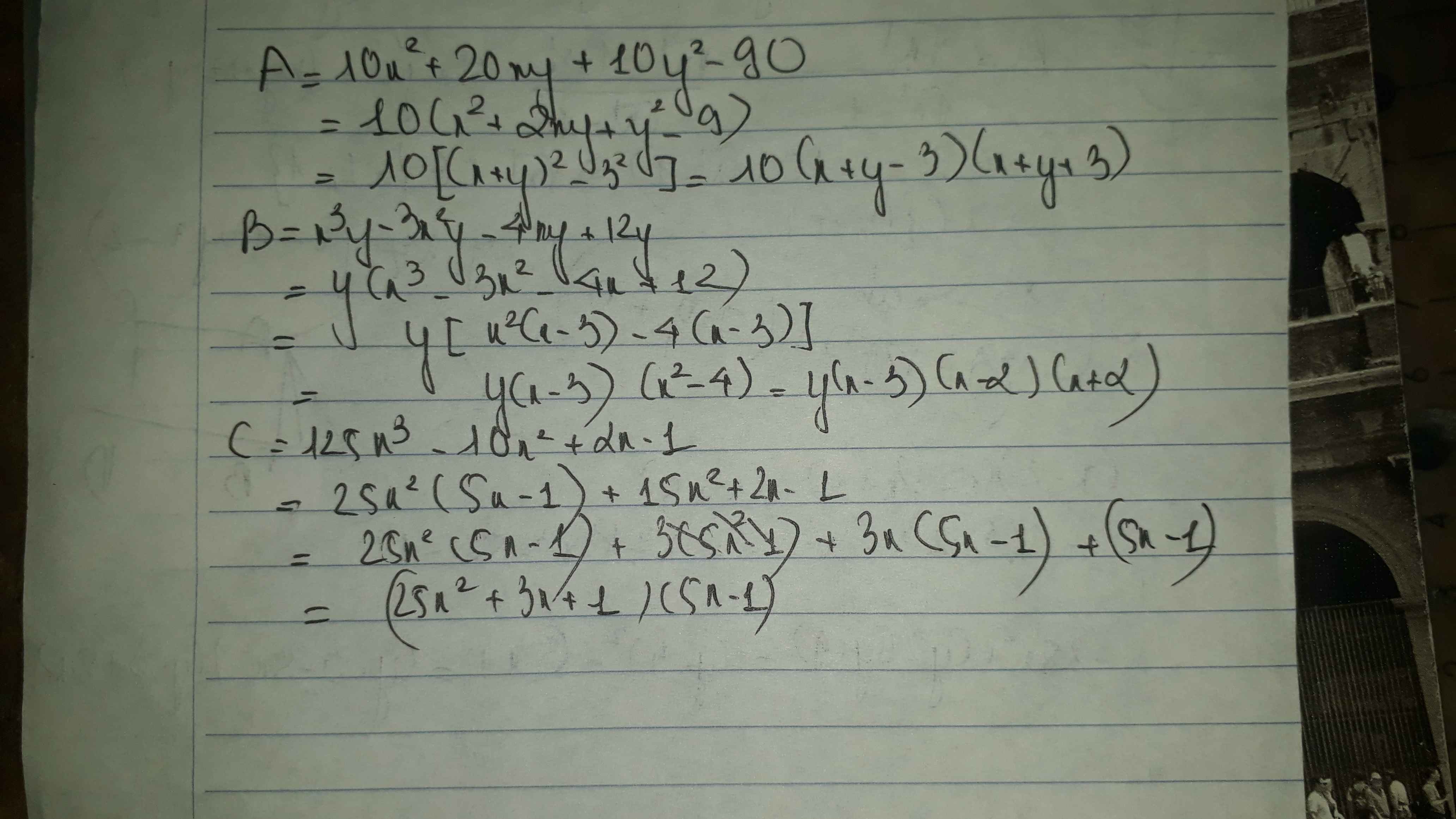(125x3 + 1) : (5x + 1)

Những câu hỏi liên quan
1.chia đa thức cho đa thức:
(125x3+1):(5x+1)
\(\text{(125x^3+1):(5x+1)}\)
\(\text{= [(5x)^3+1)]:(5x+1)}\)
\(\text{=(5x+1)(25x^2-5x+1):(5x+1)}\)
\(\text{= 25x^2-5x+1}\)
Đúng 2
Bình luận (0)
Áp dụng hằng đẳng thức đáng nhớ để thực hiện phép chia: (125x3 + 1) : (5x + 1)
(125x3 + 1) : (5x + 1)
= [(5x)3 + 1] : (5x + 1)
= (5x + 1)[(5x)2 – 5x + 1]] : (5x + 1)
= (5x)2 – 5x + 1
= 25x2 – 5x + 1
Đúng 0
Bình luận (0)
a) (x2 + 2xy + y2) : (x + y)
b) (125x3 + 1) : (5x + 1)
c) (x2 – 2xy + y2) : (y – x)
a) \(\left(x^2+2xy+y^2\right):\left(x+y\right)=\left(x+y\right)^2:\left(x+y\right)=x+y\)
b) \(=\left[\left(5x+1\right)\left(25x^2-5x+1\right)\right]:\left(5x+1\right)=25x^2-5x+1\)
c) \(=\left(y-x\right)^2:\left(y-x\right)=y-x\)
Đúng 4
Bình luận (0)
\(a,=\left(x+y\right)^2:\left(x+y\right)=x+y\\ b,=\left(5x+1\right)\left(25x^2-5x+1\right):\left(5x+1\right)=25x^2-5x+1\\ c,=\left(y-x\right)^2:\left(y-x\right)=y-x\)
Đúng 3
Bình luận (0)
Áp dụng hằng đẳng thức đáng nhớ để thực hiện phép chia:
a) (x2 + 2xy + y2) : (x + y)
b) (125x3 + 1) : (5x + 1)
c) (x2 – 2xy + y2) : (y – x)
Lời giải:
a) (x2 + 2xy + y2) : (x + y)
= (x + y)2 : (x + y)
= x + y
b) (125x3 + 1) : (5x + 1)
= [(5x)3 + 1] : (5x + 1)
= (5x + 1)[(5x)2 – 5x + 1]] : (5x + 1)
= (5x)2 – 5x + 1
= 25x2 – 5x + 1
c) (x2 – 2xy + y2) : (y – x)
= (x – y)2 : [-(x – y)]
= -(x – y)
= y – x
Hoặc (x2 – 2xy + y2) : (y – x)
= (y2 – 2yx + x2) : (y – x)
= (y – x)2 : (y – x)
= y – x
Đúng 0
Bình luận (0)
\(\text{a) (x^2 + 2xy + y^2) : (x + y)}\\ \left(x+y\right)^2:\left(x+y\right)=x+y\)
Đúng 0
Bình luận (0)
1. Viết dưới dạng
a, M= x2-100
b,N=x3+1000
c,P=125x3-1
d,Q=8x3-27
a) \(M=x^2-100=\left(x-10\right)\left(x+10\right)\)
b) \(N=x^3+1000=\left(x+10\right)\left(x^2-10x+100\right)\)
c) \(125x^3-1=\left(5x-1\right)\left(25x^2+5x+1\right)\)
d) \(8x^3-27=\left(2x-3\right)\left(4x^2+6x+9\right)\)
Đúng 1
Bình luận (0)
a, \(M=x^2-100=\left(x-10\right)\left(x+10\right)\)
b, \(N=x^3+1000=\left(x+10\right)\left(x^2-10x+100\right)\)
c, \(P=125x^3-1=\left(5x-1\right)\left(25x^2+5x+1\right)\)
d, \(Q=8x^3-27=\left(2x-3\right)\left(2x+3\right)\)
Đúng 1
Bình luận (1)
l) 5xy2- 10xyz + 5xz2
m) x3+ 3x2+ 3x + 1 - 27y3
n) x2- 6xy + 9y2
o) x3+ 6x2y + 12xy2+ 8y3
p) 125x3+ y6
q) x2 + 4xy + 4y2 - 2x - 4y + 1
\(l,=5x\left(y^2-2yz+5z\right)\\ m,=\left(x+1\right)^3-27y^3\\ =\left(x+1-3y\right)\left(x^2+2x+1+3xy+3y+9y^2\right)\\ n,=\left(x-3y\right)^2\\ o,=\left(x+2y\right)^3\\ p,=\left(5x+y^2\right)\left(25x^2-5xy^2+y^4\right)\\ q,=\left(x+2y\right)^2-2\left(x-2y\right)+1\\ =\left(x+2y-1\right)^2\)
Đúng 0
Bình luận (0)
Phân tích đa thức thành nhân tử:
A= 10x2+ 20xy + 10y - 90.
B= x3y - 3x2y - 4xy + 12y.
C= 125x3 - 10x2 + 2x - 1.
a: Ta có: \(A=10x^2+20xy+10y^2-90\)
\(=10\left(x^2+2xy+y^2-9\right)\)
\(=10\left(x+y-3\right)\left(x+y+3\right)\)
b: Ta có: \(B=x^3y-3x^2y-4xy+12y\)
\(=x^2y\left(x-3\right)-4y\left(x-3\right)\)
\(=y\left(x-3\right)\left(x-2\right)\left(x+2\right)\)
c: Ta có: \(C=125x^3-10x^2+2x-1\)
\(=\left(5x-1\right)\left(25x^2+5x+1\right)-2x\left(5x-1\right)\)
\(=\left(5x-1\right)\left(25x^2+3x+1\right)\)
Đúng 2
Bình luận (0)
Viết các đa thức sau thành tích
1, (4x2 + 4x + 1) 2, x2 – 20x + 100
3, y4 – 14y2 + 49 4, 125x3 – 64y3
Mình cần quá trình làm nữa nha, thanks
1: \(4x^2+4x+1=\left(2x+1\right)^2\)
2: \(x^2-20x+100=\left(x-10\right)^2\)
3: \(y^4-14y^2+49=\left(y^2-7\right)^2\)
4: \(125x^3-64y^3=\left(5x-4y\right)\left(25x^2+20xy+16y^2\right)\)
Đúng 0
Bình luận (0)
Bài 2: Phân tích đa thức sau thành nhân tử:
a) x4 - y4
b) x2 - 3y2
c) (3x - 2y)2 - (2x - 3y)2
d) 9(x - y)2 - 4(x + y)2
e) (4x2 - 4x + 1) - (x + 1)2
f) x3 + 27
g) 27x3 - 0,001
h) 125x3 - 1
a) \(x^4-y^4\)
\(=\left(x^2\right)^2-\left(y^2\right)^2\)
\(=\left(x^2-y^2\right)\left(x^2+y^2\right)\)
\(=\left(x+y\right)\left(x-y\right)\left(x^2+y^2\right)\)
b) \(x^2-3y^2\)
\(=x^2-\left(y\sqrt{3}\right)^2\)
\(=\left(x-y\sqrt{3}\right)\left(x+y\sqrt{3}\right)\)
c) \(\left(3x-2y\right)^2-\left(2x-3y\right)^2\)
\(=\left(3x-2y+2x-3y\right)\left(3x-2y-3x+2y\right)\)
\(=0\cdot0\)
\(=0\)
d) \(9\left(x-y\right)^2-4\left(x+y\right)^2\)
\(=\left(3x-3y\right)^2-\left(2x+2y\right)^2\)
\(=\left(3x-3y-2x-2y\right)\left(3x-3y+2x+2y\right)\)
\(=\left(x-5y\right)\left(5x-y\right)\)
e) \(\left(4x^2-4x+1\right)-\left(x+1\right)^2\)
\(=\left(2x-1\right)^2-\left(x+1\right)^2\)
\(=\left(2x-1+x+1\right)\left(2x-1-x-1\right)\)
\(=3x\left(x-2\right)\)
f) \(x^3+27\)
\(=x^3+3^3\)
\(=\left(x+3\right)\left(x^2-3x+9\right)\)
g) \(27x^3-0,001\)
\(=\left(3x\right)^3-\left(0,1\right)^3\)
\(=\left(3x-0,1\right)\left(9x^2+0,3x+0,01\right)\)
h) \(125x^3-1\)
\(=\left(5x\right)^3-1^3\)
\(=\left(5x-1\right)\left(25x^2+5x+1\right)\)
Đúng 3
Bình luận (1)
Viết dưới dạng tích: x3 – 64y3 ; 125x3 + y3
\(x^3-64=\left(x-4\right)\left(x^2+4x+16\right)\)
\(125x^3+y^3=\left(5x+y\right)\left(25x^2-5xy+y^2\right)\)
Đúng 0
Bình luận (0)