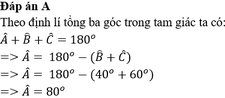Tìm x trong hình

Những câu hỏi liên quan
Tìm số đo:
a) Góc mOp trong Hình 22a;
b) Góc qPr trong Hình 22b;
c) x,y trong Hình 22c.
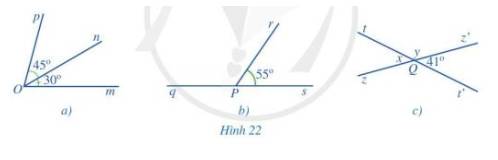
a) Vì tia On nằm trong góc mOp nên \(\widehat {mOn} + \widehat {nOp} = \widehat {mOp}\)
\(\begin{array}{l} \Rightarrow 30^\circ + 45^\circ = \widehat {mOp}\\ \Rightarrow 75^\circ = \widehat {mOp}\end{array}\)
Vậy số đo góc mOp là 75 độ
b) Ta có: \(\widehat {q\Pr } + \widehat {rPs} = 180^\circ \) (2 góc kề bù)
\(\begin{array}{l} \Rightarrow \widehat {q\Pr } + 55^\circ = 180^\circ \\ \Rightarrow \widehat {q\Pr } = 180^\circ - 55^\circ = 125^\circ \end{array}\)
Vậy số đo góc qPr là 125 độ
c) Ta có: \(\widehat {tQz} = \widehat {t'Qz'}\) ( 2 góc đối đỉnh), mà \(\widehat {t'Qz'} = 41^\circ \Rightarrow \widehat {tQz} = 41^\circ \)
\(\widehat {tQz'} + \widehat {z'Qt'} = 180^\circ \) ( 2 góc kề bù) nên \(\widehat {tQz'} + 41^\circ = 180^\circ \Rightarrow \widehat {tQz'} = 180^\circ - 41^\circ = 139^\circ \)
Vậy x = 41 \(^\circ \) ; y = 139 \(^\circ \)
Đúng 2
Bình luận (0)
Tìm x trong hình 23.
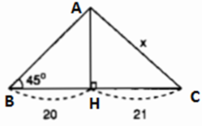
Hình 23
Kí hiệu như hình trên.
Ta có tam giác ABH là vuông cân (vì ∠B = 45o) nên AH = 20.
Áp dụng định lí Pitago trong tam giác vuông AHC có:
x2 = AH2 + HC2 = 202 + 212 = 841
=> x = √841 = 29
Đúng 0
Bình luận (0)
Tìm x trong hình 23.
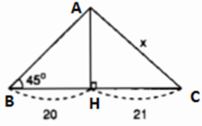
Hình 23
Kí hiệu như hình trên.
Ta có tam giác ABH là vuông cân (vì ∠B = 45o) nên AH = 20.
Áp dụng định lí Pitago trong tam giác vuông AHC có:
x2 = AH2 + HC2 = 202 + 212 = 841
=> x = √841 = 29
Đúng 0
Bình luận (0)
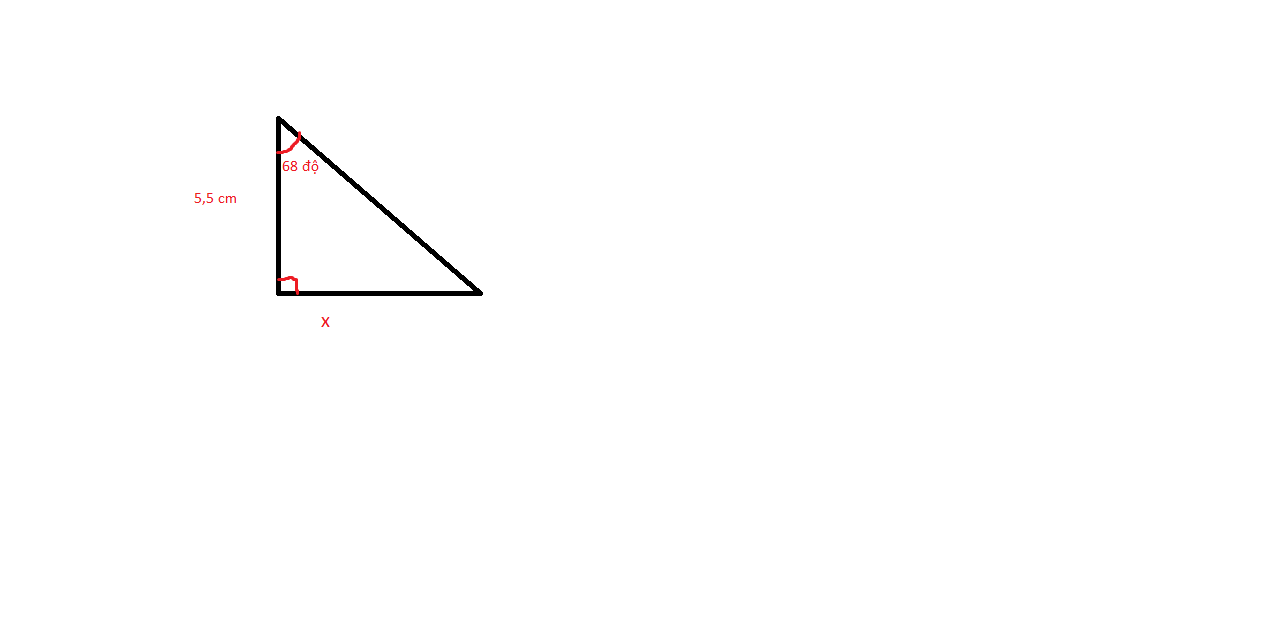 tìm độ dài x trong hình
tìm độ dài x trong hình
Tìm x trong hình vẽ bên
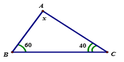
A. 80 °
B. 70 °
C. 100 °
D. 90 °
Bài 4: Tìm x trong hình
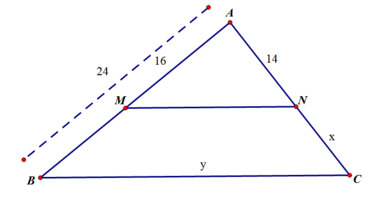
bạn phải cho điều kiện MN//BC nữa thì mới áp dụng định lý Ta-lét được
Đúng 1
Bình luận (0)
Ta có:MB=AB-AM=24-16=8
Áp dụng định lý Ta-lét ta có:
\(\dfrac{AM}{MB}=\dfrac{AN}{NC}\\ \Rightarrow\dfrac{16}{8}=\dfrac{14}{x}\\ \Rightarrow2=\dfrac{14}{x}\\ \Rightarrow x=7\)
Đúng 0
Bình luận (0)
Coi như đã song song, theo định lý Talet:
\(\dfrac{AM}{AB}=\dfrac{AN}{AC}\Leftrightarrow\dfrac{16}{24}=\dfrac{14}{14+x}\)
\(\Leftrightarrow\dfrac{2}{3}=\dfrac{14}{14+x}\Rightarrow2\left(14+x\right)=42\)
\(\Rightarrow2x=14\Rightarrow x=7\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
A B D C x 5,1cm 3cm 5cm cho tam giác ABC có AD là phân giác trong của góc A . Tìm x trong hình vẽ sau với đọ dài cho sẵn trong hình
Đọc tiếp
cho tam giác ABC có AD là phân giác trong của góc A . Tìm x trong hình vẽ sau với đọ dài cho sẵn trong hình
AD là tia phân giác của ∠BAC
\(\Rightarrow\dfrac{AB}{AC}=\dfrac{BD}{CD}\Leftrightarrow\dfrac{x}{5}=\dfrac{5,1}{3}\Leftrightarrow x=8,5\left(cm\right)\)
Đúng 2
Bình luận (0)
tìm số đo x trong hình bên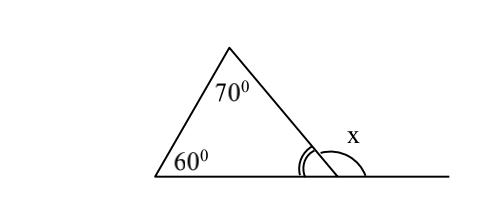
Ta có: △ABC=180o
=> góc C=180o-(70o+60o)=50o
=> C1+C2=180o
=>C2=180o-50o=130o
hay x=130o
Đúng 2
Bình luận (0)
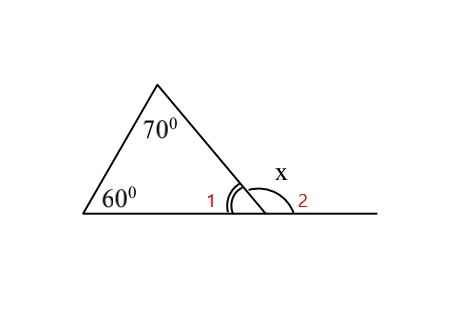
Ta chia \(\widehat{x}:\widehat{x1};\widehat{x2}\)
\(\Rightarrow\widehat{x1}=50^o\)
\(\widehat{x1}+\widehat{x2}=180^o\) (kề bù)
\(\Rightarrow\widehat{x2}=180^o-50^o=130^o\)
Đúng 1
Bình luận (1)
Xem thêm câu trả lời
Tìm x; y trong hình vẽ sau: A. x 30; y 28 B. x
2
481
; y
225
8
C. x 18; y 40 D. x 40; y 18
Đọc tiếp
Tìm x; y trong hình vẽ sau:
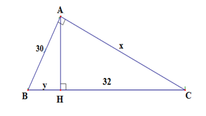
A. x = 30; y = 28
B. x = 2 481 ; y = 225 8
C. x = 18; y = 40
D. x = 40; y = 18
Ta có: BC = BH + HC = y + 32
Áp dụng hệ thức lượng A B 2 = B H . B C trong tam giác vuông ABC ta có:
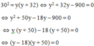
⇔ y − 18 = 0 y + 50 = 0 ⇔ y = 18 N y = − 50 L
Suy ra y = 18 => BC = 18 + 32 = 50
Áp dụng hệ thức lượng A C 2 = C H . B C ta có:
![]()
Vậy c = 40; y = 18
Đáp án cần chọn là: D
Đúng 0
Bình luận (0)
Tìm x, y trong hình vẽ sau:
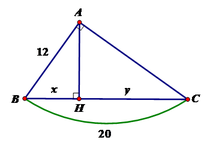
A. x = 7,2; y = 11,8
B. x = 7; y = 12
C. x = 7,2; y = 12,8
D. x = 7,2; y = 12
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
A B 2 = B H . B C ⇔ B H = A B 2 B C = 144 20 = 7 , 2 => CH = BC – BH = 20 – 7,2 = 12,8
Vậy x = 7,2; y = 12,8
Đáp án cần chọn là: C
Đúng 0
Bình luận (0)