Hàm số nghịch biến trên khoảng
A. (-∞;0)
B. (0;+∞)
C. R{0}
D. R
Cho hàm số . Khẳng định nào sau đây là khẳng định sai?
A. Hàm số nghịch biến trên khoảng (-∞;-1)
B. Hàm số nghịch biến trên khoảng (-1;\(\dfrac{1}{2}\))
C. Hàm số đồng biến trên mỗi khoảng (-∞;-1) và (\(\dfrac{1}{2}\);+∞)
D. Hàm số nghịch biến trên khoảng (-1;\(\dfrac{1}{2}\))và đồng biến trên khoảng(\(\dfrac{1}{2}\);+∞)
cho hàm số y= x3. Khẳng định nào sau đây đúng?
A. Hàm số nghịch biến trên \(R\)
B. Hàm số đồng biến trên \(R\)
C. Hàm số đồng biến trên (-∞;0)
D. Hàm số nghịch biến trên (0;+∞)
Câu 4. Cho hàm số \(y = x^4 - 2x^2 -3\). Mệnh đề nào sau đây là mệnh đề đúng?
A. Hàm số nghịch biến trên \((-1; 0).\)
B. Hàm số đồng biến trên \((-\infty;0).\)
C. Hàm số nghịch biến trên \((-1; 1).\)
D. Hàm số nghịch biến trên \((0; +\infty).\)
\(y'=0\Leftrightarrow4x^3-4x=0\Leftrightarrow4x\left(x^2-1\right)=0\\ \Leftrightarrow x=\pm1.và.x=0\)
\(HSNB:\left(-\infty;-1\right)\cup\left(0;1\right)\\ HSĐB:\left(-1;0\right)\cup\left(1;+\infty\right)\)
Cho hàm số:
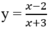
Khẳng định nào sau đây là đúng?
A. Hàm số đồng biến trên từng khoảng xác định;
B. Hàm số đồng biến trên khoảng (- ∞ ;+ ∞ );
C. Hàm số nghịch biến trên từng khoảng xác định;
D. Hàm số nghịch biến trên khoảng (- ∞ ;+ ∞ ).
Cho hàm số y=f(x) xác định trên ℝ và có đồ thị của hàm số f’(x) và các khẳng định sau:
(1). Hàm số y=f(x) đồng biến trên khoảng 1 ; + ∞
(2). Hàm số y=f(x) nghịch biến trên khoảng - ∞ ; - 2
(3). Hàm số y=f(x) nghịch biến trên khoảng - 2 ; 1 .
(4). Hàm số y = f x 2 đồng biến trên khoảng - 1 ; 0
(5). Hàm số y = f x 2 nghịch biến trên khoảng (1;2)

Số khẳng định đúng là
A. 4
B. 3
C. 2
D. 5
Cho hàm số: y = x - 2 x + 3
Khẳng định nào sau đây là đúng?
A. Hàm số đồng biến trên từng khoảng xác định;
B. Hàm số đồng biến trên khoảng (- ∞ ;+ ∞ );
C. Hàm số nghịch biến trên từng khoảng xác định;
D. Hàm số nghịch biến trên khoảng (- ∞ ;+ ∞ ).
1. Cho hàm số y =f(x) có đạo hàm f'(x) = (x^2 -1)(x-2)^2(x-3) . Hàm số đồng biến ; nghịch biến trên khoảng nào? 2. Cho hàm số y = x^4 -2x^2 . Hàm số đồng biến ; nghịch biến trên khoảng nào?
1.
\(f'\left(x\right)=\left(x^2-1\right)\left(x-2\right)^2\left(x-3\right)\) có các nghiệm bội lẻ \(x=\left\{-1;1;3\right\}\)
Sử dụng đan dấu ta được hàm đồng biến trên các khoảng: \(\left(-1;1\right);\left(3;+\infty\right)\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;-1\right);\left(1;3\right)\)
2.
\(y'=4x^3-4x=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=0\\x=1\end{matrix}\right.\)
Lập bảng xét dấu y' ta được hàm đồng biến trên \(\left(-1;0\right);\left(1;+\infty\right)\)
Hàm nghịch biến trên \(\left(-\infty;-1\right);\left(0;1\right)\)
cho hàm số y=f(x)=-x^2-2x+1. Mệnh đề nào sau đây là đúng? A. Hàm số nghịch biến trên khoảng (-1;+vô cực) B. Hàm số nghịch biến trên khoảng (-vô cực;-1) C. Hàm số đồng biến trên khoảng (-1;+vô cực) D. Hàm số đồng biến trên khoảng (-vô cực;0)
B. Hàm số nghịch biến trên khoảng \(\left(-\infty;-1\right)\)
Cho hàm số có f đạo hàm trên khoảng I. Xét các mệnh đề sau:
(I). Nếu , thì hàm f '(x) < 0 "x ∈ I số nghịch biến trên I
(II). Nếu , f '(x) ≤ 0 "x ∈ I (dấu bằng chỉ xảy ra tại một số hữu hạn điểm trên I ) thì hàm số nghịch biến trên I
(III). Nếu , thì hàm f '( x) ≤ 0 "x ∈ I số nghịch biến trên khoảng I
(IV). Nếu , f '(x) ≤ 0 "x ∈ I và f '(x) = 0 tại vô số điểm trên thì hàm I số không f thể nghịch biến trên khoảng I
Trong các mệnh đề trên. Mệnh đề nào đúng, mệnh đề nào sai?
A. I, II và IV đúng, còn III sai.
B. I, II, III và IV đúng.
C. I và II đúng, còn III và IV sai.
D. I, II và III đúng, còn IV sai.
Đáp án là C
Câu III sai vì thiếu dấu bằng chỉ xảy ra tại một số hữu hạn điểm trên I
Câu IV sai vì có thể vô số điểm trên I xuất hiện rời rạc thì vẫn có thể nghịch biến trên khoảng I
cho hàm số y = 2x2 - (m - 1 )x +3, m là tham số
a. tìm khoảng đồng biến, nghịch biến của hàm số
b/ tìm các giái trị của m để hàm số đồng biến trên khoảng 1;+∞
c. tìm m để hàm số nghịch biến trên khoàng -4;8
d. tìm m để giá trị nhỏ nhất của hàm số là 9