Các câu hỏi tương tự
Câu 23 (NB) Hàm số nghịch biến trên khoảng : A. (-∞;0)
A. (-∞;0)
B (0;+∞)
C. R\{0}
D. R
Câu 1: Cho hàm số y=x-1 Trong các khẳng định sau, khẳng định nào sai?
A. Đồ thị cắt: trục hoành tại A ( 1;0 ) , trục tung tại B (0; -1) .
B.Hàm số đồng biến trên R .
C. Đồ thị không qua gốc tọa độ.
D.Hàm số nghịch biến trên R
cho hàm số y=f(x)=-x^2-2x+1. Mệnh đề nào sau đây là đúng? A. Hàm số nghịch biến trên khoảng (-1;+vô cực) B. Hàm số nghịch biến trên khoảng (-vô cực;-1) C. Hàm số đồng biến trên khoảng (-1;+vô cực) D. Hàm số đồng biến trên khoảng (-vô cực;0)
Tập xác định của hàm số
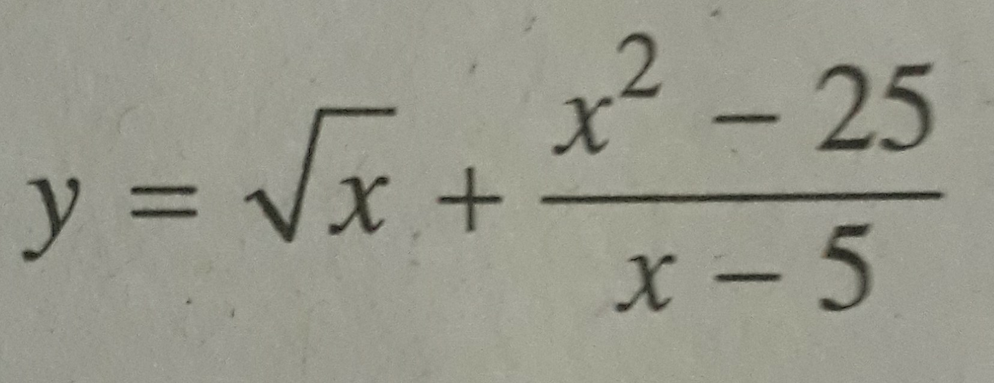
A. R B. [0; +∞) C. [0; +∞) \ {5} D. [0; 5)
Câu 48. Cho y|x+1|+|x−2|và các mệnh đề 1)Hàm số tăng lên trên(-1,+∞)2)Hàm số không đổi trên[−1;2)3) Hàm số giảm trên(-∞,-1)4) Hàm số giảm trên (-2,+∞)Hỏi có bao nhiêu mệnh đề đúng?A. 0 B. 1 C. 2 D. 3Câu 49. Hàm số y-√|2x+3|nghịch biến trên khoảng.A.(-dfrac{3}{2},+infty)B.(-∞,-dfrac{3}{2})C. RD.Cả 3 đáp án đều sai
Đọc tiếp
Câu 48. Cho y=|x+1|+|x−2|và các mệnh đề
1)Hàm số tăng lên trên(-1,+∞)
2)Hàm số không đổi trên[−1;2)
3) Hàm số giảm trên(-∞,-1)
4) Hàm số giảm trên (-2,+∞)
Hỏi có bao nhiêu mệnh đề đúng?
A. 0 B. 1 C. 2 D. 3
Câu 49. Hàm số y=-√|2x+3|nghịch biến trên khoảng.
A.(\(-\dfrac{3}{2},+\infty\))
B.(-∞,\(-\dfrac{3}{2}\))
C. R
D.Cả 3 đáp án đều sai
Câu 94. Cho hàm số y =x2 đồng biến trên khoảng
A.R B.(0,+∞) C.R\{0} D.(-∞,0)
Câu 95. Đỉnh của parabol y=-x2 +2x+3 có tọa độ là bao nhiêu.
Câu 96. Hàm số y=-x2 +2x+3 đồng biến trên khoảng:
A.(-1,+∞)
B.(-∞,-1)
C.(1,+∞)
D.(-∞,1)
Chỉ ra khoảng đồng biến, nghịch biến của hàm số : y = ax + b, trong mỗi trường hợp a > 0 ; a < 0.
Chỉ ra khoảng đồng biến, nghịch biến của hàm số: y = ax2 + bx + c, trong mỗi trường hợp a > 0 ; a < 0.
Có bao nhiêu giá trị nguyên của m thuộc đoạn [0; 3] để hàm số y = ( m 2 − 1)x đồng biến trên R.
A. 0
B. 1
C. 2
D. Kết quả khác
Xét tính đồng biến, nghịch biến của hàm số trên các khoảng tương ứng
y = -2x + 3 trên R








