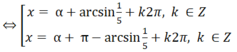a,Pt \(\Leftrightarrow cosx-sinx=\dfrac{1}{2}\)

\(\Leftrightarrow\sqrt{2}cos\left(x+\dfrac{\pi}{4}\right)=\dfrac{1}{2}\)

\(\Leftrightarrow cos\left(x+\dfrac{\pi}{4}\right)=\dfrac{1}{2\sqrt{2}}\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{4}+arc.cos\left(\dfrac{1}{2\sqrt{2}}\right)+k2\pi\\x=-\dfrac{\pi}{4}-arc.cos\left(\dfrac{1}{2\sqrt{2}}\right)+k2\pi\end{matrix}\right.\) ,\(k\in Z\)

b) Pt \(\Leftrightarrow\dfrac{4}{5}cosx-\dfrac{3}{5}sinx=\dfrac{3}{5}\)

Đặt \(cosa=\dfrac{4}{5}\Rightarrow sina=\dfrac{3}{5}\)

Pttt:\(cosx.cosa-sina.sinx=\dfrac{3}{5}\)

\(\Leftrightarrow cos\left(x+a\right)=\dfrac{3}{5}\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-a+arc.cos\left(\dfrac{3}{5}\right)+2k\pi\\x=-a-arc.cos\left(\dfrac{3}{5}\right)+2k\pi\end{matrix}\right.\)(\(k\in Z\))

Vậy...

c) Pt\(\Leftrightarrow\dfrac{3}{5}cos3x+\dfrac{4}{5}.sin3x=1\)

Đặt \(cosa=\dfrac{3}{5}\Rightarrow sina=\dfrac{4}{5}\)

Pttt:\(cos3x.cosa+sin3a.sina=1\)

\(\Leftrightarrow cos\left(3x-a\right)=1\)

\(\Leftrightarrow x=\dfrac{a}{3}+\dfrac{k2\pi}{3}\)(\(k\in Z\))

Vậy...

1)\(1+2sinx=2cosx\)

\(\Leftrightarrow cosx-sinx=\dfrac{1}{2}\)

\(\Leftrightarrow\left(cosx-sinx\right)^2=\dfrac{1}{4}\)

\(\Leftrightarrow cosx^2+sinx^2-2cosxsinx=\dfrac{1}{4}\)

\(\Leftrightarrow1-2cosxsinx=\dfrac{1}{4}\)

\(\Leftrightarrow2cosxsinx=\dfrac{3}{4}\)

\(\Leftrightarrow sin2x=\dfrac{3}{4}\)

\(\Rightarrow\left\{{}\begin{matrix}x=arcsin\dfrac{3}{8}+k\pi\\x=\pi-arcsin\dfrac{3}{8}+k\pi\end{matrix}\right.\) \(\left(K\in Z\right)\)

b) \(4cosx-3sinx=3\)

\(\Leftrightarrow\dfrac{4}{5}cosx-\dfrac{3}{5}sinx=\dfrac{3}{5}\)

Đặt \(cosa=\dfrac{3}{5},sina=\dfrac{4}{5}\)

Khi đó:

\(sinacosx-cosasinx=\dfrac{3}{5}\)

\(\Leftrightarrow sin\left(a-x\right)=\dfrac{3}{5}\)

\(\Leftrightarrow\left\{{}\begin{matrix}a-x=arcsin\dfrac{3}{5}+k2\pi\\a-x=\pi-arcsin\dfrac{3}{5}+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=a-arcsin\dfrac{3}{5}+k2\pi\\x=a-\pi-arcsin\dfrac{3}{5}+k2\pi\end{matrix}\right.\) \(\left(k\in Z\right)\)

3)\(3cos3x+4sin3x=5\)

\(\Leftrightarrow\dfrac{3}{5}cos3x+\dfrac{4}{5}sin3x=1\)

Đặt \(sina=\dfrac{3}{5},cosa=\dfrac{4}{5}\)

khi đó: \(sinacos3x+cosasin3x=1\)

\(\Leftrightarrow sin\left(a+3x\right)=\dfrac{\pi}{2}\)

\(\Leftrightarrow3x=\dfrac{\pi}{2}-a+k2\pi\)

\(\Leftrightarrow x=\dfrac{\pi}{6}-\dfrac{1}{3}a+k\dfrac{2}{3}\pi\),\(k\in Z\)

Chúc bạn học tốt^^

a: -1<=sin x<=1

=>-1+3<=sin x+3<=1+3

=>2<=sinx+3<=4

=>\(\dfrac{1}{2}>=\dfrac{1}{sinx+3}>=\dfrac{1}{4}\)

=>\(2>=\dfrac{4}{sinx+3}>=1\)

=>\(-2< =-\dfrac{4}{sinx+3}< =-1\)

=>-2+3<=y<=-1+3

=>1<=y<=2

y=1 khi \(\dfrac{-4}{sinx+3}+3=1\)

=>\(\dfrac{-4}{sinx+3}=-2\)

=>sinx+3=2

=>sin x=-1

=>x=-pi/2+k2pi

y=3 khi sin x=1

=>x=pi/2+k2pi

b: -1<=cosx<=1

=>4>=-4cosx>=-4

=>9>=-4cosx+5>=1

=>2/9<=2/5-4cosx<=2

=>2/9<=y<=2

\(y_{min}=\dfrac{2}{9}\) khi \(\dfrac{2}{5-4cosx}=\dfrac{2}{9}\)

=>\(5-4\cdot cosx=9\)

=>4*cosx=4

=>cosx=1

=>x=k2pi

y max khi cosx=-1

=>x=pi+k2pi

c: \(0< =cos^2x< =1\)

=>\(0< =2\cdot cos^2x< =2\)

=>\(-1< =y< =2\)

y min=-1 khi cos^2x=0

=>x=pi/2+kpi

y max=2 khi cos^2x=1

=>sin^2x=0

=>x=kpi

a: tan x=căn 3

=>sin x/cosx=căn 3

=>sin x=cosx*căn 3

\(A=\dfrac{\left(cosx\cdot\sqrt{3}\right)^2}{\left(cosx\cdot\sqrt{3}\right)^2-cos^2x}=\dfrac{3}{3-1}=\dfrac{3}{2}\)

b: cot x=-căn 3

=>cosx=-sinx*căn 3

\(A=\dfrac{sinx+4\cdot sinx\cdot\sqrt{3}}{2\cdot sinx+sinx\cdot\sqrt{3}}=\dfrac{1+4\sqrt{3}}{2+\sqrt{3}}=\left(4\sqrt{3}+1\right)\left(2-\sqrt{3}\right)\)

=8căn 3-12+2-căn 3

=7căn 3-10

Lời giải:

\(A=\frac{1}{\frac{\sin ^2x-\cos ^2x}{\sin ^2x}}=\frac{1}{1-(\frac{\cos x}{\sin x})^2}=\frac{1}{1-(\frac{1}{\tan x})^2}=\frac{1}{1-(\frac{1}{\sqrt{3}})^2}=\frac{3}{2}\)

\(A=\frac{\sin x-4\cos x}{2\sin x-\cos x}=\frac{1-4.\frac{\cos x}{\sin x}}{2-\frac{\cos x}{\sin x}}=\frac{1-4\cot x}{2-\cot x}=\frac{1-4.(-\sqrt{3})}{2-(-\sqrt{3})}=-10+7\sqrt{3}\)

\(A=\frac{3sinx-4cosx}{cosx+2sinx}=\frac{\frac{3sinx}{cosx}-4}{1+\frac{2sinx}{cosx}}=\frac{3tanx-4}{1+2tanx}=\frac{3.5-4}{1+2.5}=...\)

\(B=\frac{\frac{sinx}{cos^3x}+\frac{sin^3x}{cos^3x}}{\frac{3cos^3x}{cos^3x}+\frac{cosx}{cos^3x}}=\frac{tanx.\frac{1}{cos^2x}+tan^3x}{3+\frac{1}{cos^2x}}=\frac{tanx\left(1+tan^2x\right)+tan^3x}{3+\left(1+tan^2x\right)}=\frac{5\left(1+5^2\right)+5^3}{3+1+5^2}=...\)

câu d chỗ mình viết sai là căn nhé

3 sin 2 x   +   4 cos x   -   2   =   0

Answer:

\(\sin x+4\cos x=2+\sin2x\)

\(\Leftrightarrow\sin x-2+4\cos x-2\sin x\cos x=0\)

\(\Leftrightarrow\sin x-2+2\cos x\left(2-\sin x\right)=0\)

\(\Leftrightarrow\left(\sin x-2\right)\left(1-2\cos x\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}\sin x=2\text{(Loại)}\\\cos x=\frac{1}{2}\end{cases}}\)

\(\Leftrightarrow x=\pm\frac{\text{π}}{3}+k2\text{π}\left(k\inℤ\right)\)

3sinx – 4cosx = 1 ⇔ 3/5sinx - 4/5cosx = 1/5.

⇔ sin(x – α) = 1/5 (với cosα = 3/5 , sinα = 4/5)