bài khó quá mn ai giúp em vs được ko ạ
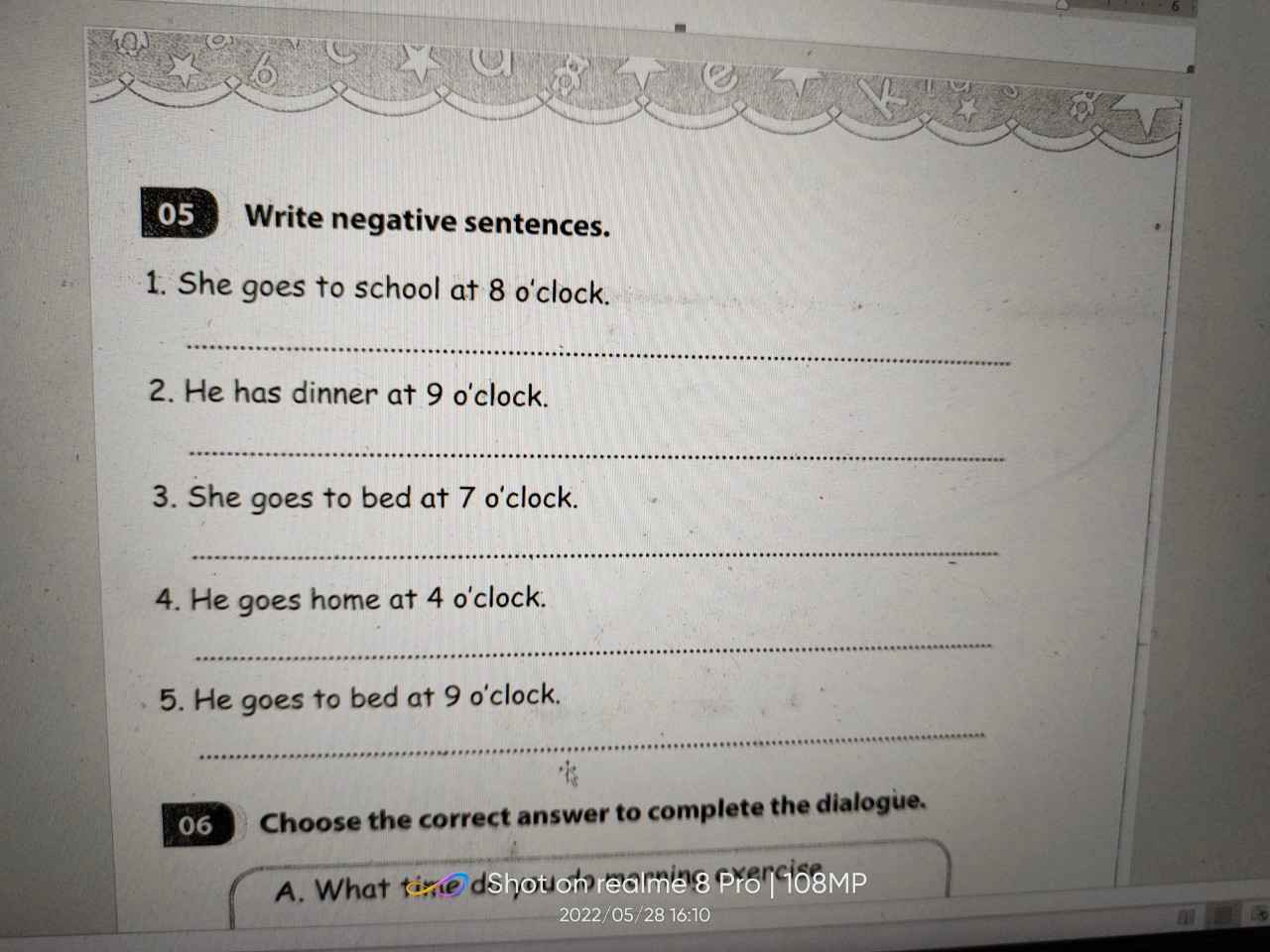
mn giúp em vs ạ. bài này em khó hiểu quá ạ
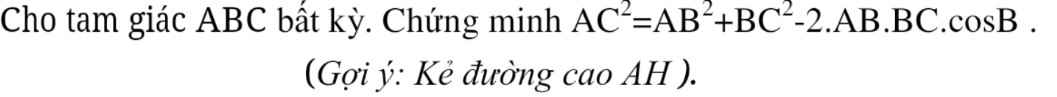
Kẻ AH⊥BC
ta có: \(VP=AB^2+BC^2-2.AB.BC.cosB=AB^2+BC^2-2.AB.BC.\dfrac{BH}{AB}=AB^2+BC^2-2.BH.BC=AB^2-BH^2+BC^2-2.BH.BC+BH^2=AH^2+\left(BC-BH\right)^2=AH^2+CH^2=AC^2=VT\)
Mn giúp em bài 11c và bài 4f với ạ mai em nộp rồi
Riêng bài 4f thì em có tìm được 1 dạng giải nhưng khó hiểu quá, ai có cách nào dễ hiểu hơn thì giúp em với

11c.
Từ đề bài ta có:
\(\left\{{}\begin{matrix}\dfrac{16a-b^2}{4a}=\dfrac{9}{2}\\16a+4b+4=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2b^2=-4a\\b=-4a-1\end{matrix}\right.\)
\(\Rightarrow2b^2-b=1\Leftrightarrow2b^2-b-1=0\Rightarrow\left[{}\begin{matrix}b=1\Rightarrow a=-\dfrac{1}{2}\\b=-\dfrac{1}{2}\Rightarrow a=-\dfrac{1}{8}\end{matrix}\right.\)
Có 2 parabol thỏa mãn: \(\left[{}\begin{matrix}y=-\dfrac{1}{2}x^2+x+4\\y=-\dfrac{1}{8}x^2-\dfrac{1}{2}x+4\end{matrix}\right.\)
4f.
Từ đề bài ta có:
\(\left\{{}\begin{matrix}1+b+c=0\\\dfrac{4c-b^2}{4}=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}c=-b-1\\c=\dfrac{b^2}{4}-1\end{matrix}\right.\)
\(\Rightarrow\dfrac{b^2}{4}+b=0\)
\(\Rightarrow\left[{}\begin{matrix}b=0\Rightarrow c=-1\\b=-4\Rightarrow c=3\end{matrix}\right.\)
Có 2 parabol thỏa mãn: \(\left[{}\begin{matrix}y=x^2-1\\y=x^2-4x+3\end{matrix}\right.\)
Ai biết bài"Chữa lỗi quan hệ từ" theo Vnen ý... soạn bài ý khó quá...ai giúp vs ạ..!!!
Soạn bài: Chữa lỗi về quan hệ từ
I. Các lỗi thường gặp về quan hệ từ
1. Lỗi thiếu quan hệ từ
a. Hai câu đã cho sai vì thiếu quan hệ từ.
b. Chữa lại:
Đừng nên nhìn hình thức mà đánh giá kẻ khác.
Câu tục ngữ này chỉ đúng với xã hội xưa, còn ngày nay thì không đúng.
2. Lỗi dùng quan hệ từ không thích hợp về nghĩa
a. Các quan hệ từ và, để dùng không đúng nghĩa, không thể hiện chính xác mối quan hệ giữa các thành phần câu.
b. Chữa: thay và bằng nhưng, thay để bằng vì.
3. Lỗi thừa quan hệ từ
a. Các câu này đều thiếu chủ ngữ. Các quan hệ từ qua, về ở đầu câu đã biến chủ ngữ của câu thành thành phần trạng ngữ. Đây là lỗi thừa quan hệ từ.
b. Cách chữa là bỏ quan hệ từ để khôi phục thành phần chủ ngữ cho câu:
Câu ca dao "Công cha như núi Thái Sơn, Nghĩa mẹ như nước trong nguồn chảy ra" cho ta thấy công lao to lớn của cha mẹ đối với con cái.
Hình thức có thể làm tăng giá trị nội dung đồng thời hình thức có thể làm thấp giá trị nội dung.
4. Lỗi dùng quan hệ từ mà không có tác dụng liên kết
a. Không những giỏi về môn toán, không những giỏi về môn Văn; ... không thích với chị. Quan hệ từ không những ... đòi hỏi phải có quan hệ từ mà còn... đi kèm. Quan hệ từ với trong trường hợp này thiết lập quan hệ giữa không thích và chị là không hợp lí, không tương ứng với vế trước.
b. Có thể chữa:
Nam là một học sinh giỏi toàn diện. Bạn ấy không những giỏi về môn toán, môn văn mà còn giỏi về nhiều môn khác.
Nó thích tâm sự với mẹ, không thích tâm sự với chị.
II. Luyện tập
Câu 1:
Nó chăm chú nghe kể chuyện từ đầu đến cuối.
Con xin báo một tin vui để cha mẹ mừng.
Câu 2: Thay các quan hệ từ dùng sai:
Ngày nay, chúng ta cũng có quan niệm như cha ông ta ngày xưa, lấy đạo đức, tài năng làm trọng.
Dù nước sơn có đẹp đến mấy mà chất gỗ không tốt thì đồ vật cũng không bền được.
Không nên chỉ đánh giá con người về hình thức bên ngoài mà nên đánh giá con người về những hành động, cử chỉ, cách đối xử của họ
Câu 3: Cách chữa chung cho loại lỗi này là bỏ các quan hệ từ để khôi phục chủ ngữ cho câu. Có thể sửa:
Bản thân em còn nhiều thiếu sót, em hứa sẽ tích cực sửa chữa.
Câu tục ngữ "Lá lành đùm lá rách" cho em hiểu đạo lí làm người là phải giúp đỡ người khác.
Bài thơ này đã nói lên tình cảm của Bác Hồ đối với thiếu nhi.
Câu 4: Các câu sai: (c), (e), (g), (i), có thể sửa như sau:
Chúng ta phải sống thế nào để chan hoà với mọi người. (bỏ từ cho)
Phải luôn luôn chống tư tưởng chỉ bo bo bảo vệ quyền lợi của bản thân mình. (sửa lại cụm bản thân của mình)
Sống trong xã hội phong kiến đương thời, nhân dân ta bị áp bức bóc lột vô cùng tàn bạo. (bỏ từ của)
Trời mà mưa thì con đường này sẽ rất trơn. (quan hệ từ giá chỉ dùng để biểu thị điều kiện thuận lợi).
ai giúp em làm bài này với ạ khó quá :(

Giúp em với ạ bài khó quá không làm được . Em cảm ơn ạ !
a: |x|=5,6
=>\(\left[{}\begin{matrix}x=5,6\\x=-5,6\end{matrix}\right.\)
c: \(\left|x\right|=3\dfrac{1}{5}\)
=>\(\left|x\right|=3,2\)
=>\(\left[{}\begin{matrix}x=3,2\\x=-3,2\end{matrix}\right.\)
d: |x|=-2,1
mà -2,1<0
nên \(x\in\varnothing\)
d: |x-3,5|=5
=>\(\left[{}\begin{matrix}x-3,5=5\\x-3,5=-5\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=8,5\\x=-1,5\end{matrix}\right.\)
e: \(\left|x+\dfrac{3}{4}\right|-\dfrac{1}{2}=0\)
=>\(\left|x+\dfrac{3}{4}\right|=\dfrac{1}{2}\)
=>\(\left[{}\begin{matrix}x+\dfrac{3}{4}=\dfrac{1}{2}\\x+\dfrac{3}{4}=-\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{4}\\x=-\dfrac{5}{4}\end{matrix}\right.\)
f: \(\left|4x\right|-\left|-13,5\right|=\left|2\dfrac{1}{4}\right|\)
=>\(4\left|x\right|=2,25+13,5=15,75\)
=>\(\left|x\right|=\dfrac{63}{16}\)
=>\(x=\pm\dfrac{63}{16}\)
g: \(\dfrac{5}{6}-\left|2-x\right|=\dfrac{1}{3}\)
=>\(\dfrac{5}{6}-\left|x-2\right|=\dfrac{1}{3}\)
=>\(\left|x-2\right|=\dfrac{5}{6}-\dfrac{1}{3}=\dfrac{1}{2}\)
=>\(\left[{}\begin{matrix}x-2=\dfrac{1}{2}\\x-2=-\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=\dfrac{3}{2}\end{matrix}\right.\)
h: \(\left|x-\dfrac{2}{5}\right|+\dfrac{1}{2}=\dfrac{3}{4}\)
=>\(\left|x-\dfrac{2}{5}\right|=\dfrac{3}{4}-\dfrac{1}{2}=\dfrac{1}{4}\)
=>\(\left[{}\begin{matrix}x-\dfrac{2}{5}=\dfrac{1}{4}\\x-\dfrac{2}{5}=-\dfrac{1}{4}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{4}+\dfrac{2}{5}=\dfrac{13}{20}\\x=-\dfrac{1}{4}+\dfrac{2}{5}=\dfrac{-5+8}{20}=\dfrac{3}{20}\end{matrix}\right.\)
i: \(\left|5-3x\right|+\dfrac{2}{3}=\dfrac{1}{6}\)
=>\(\left|3x-5\right|=\dfrac{1}{6}-\dfrac{2}{3}=\dfrac{1}{6}-\dfrac{4}{6}=-\dfrac{3}{6}=-\dfrac{1}{2}< 0\)
=>\(x\in\varnothing\)
k: \(-2,5+\left|3x+5\right|=-1,5\)
=>|3x+5|=-1,5+2,5=1
=>\(\left[{}\begin{matrix}3x+5=1\\3x+5=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}3x=-4\\3x=-6\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=-\dfrac{4}{3}\\x=-2\end{matrix}\right.\)
m: \(\dfrac{1}{5}-\left|\dfrac{1}{5}-x\right|=\dfrac{1}{5}\)
=>\(\left|\dfrac{1}{5}-x\right|=\dfrac{1}{5}-\dfrac{1}{5}=0\)
=>\(\dfrac{1}{5}-x=0\)
=>\(x=\dfrac{1}{5}\)
n: \(-\dfrac{22}{15}x+\dfrac{1}{3}=\left|-\dfrac{2}{3}+\dfrac{1}{5}\right|\)
=>\(-\dfrac{22}{15}x+\dfrac{1}{3}=\dfrac{2}{3}-\dfrac{1}{5}\)
=>\(-\dfrac{22}{15}x=\dfrac{1}{3}-\dfrac{1}{5}=\dfrac{2}{15}\)
=>-22x=2
=>\(x=-\dfrac{1}{11}\)
Bài khó quá nên nhờ ai học giỏi làm giúp em ạ! Em đang cần gấp :(
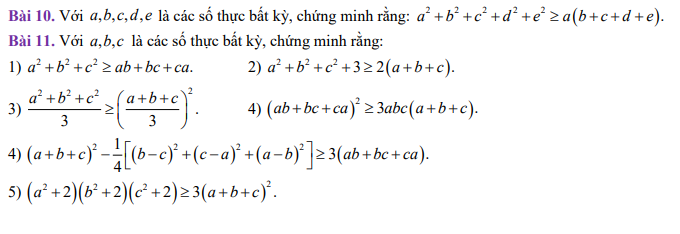
\(10,\\ a^2+b^2+c^2+d^2+e^2\ge a\left(b+c+d+e\right)\\ \Leftrightarrow4a^2+4b^2+4c^2+4d^2+4e^2\ge4ab+4ac+4ad+4ae\\ \Leftrightarrow\left(a^2-4ab+4b^2\right)+\left(a^2-4ac+4c^2\right)+\left(a^2-4ad+4d^2\right)+\left(a^2-4ae+4e^2\right)\ge0\\ \Leftrightarrow\left(a-2b\right)^2+\left(a-2c\right)^2+\left(a-2d\right)^2+\left(a-2e\right)^2\ge0\left(luôn.đúng\right)\)
Dấu \("="\Leftrightarrow\dfrac{a}{2}=b=c=d=e\)
\(4,\Leftrightarrow a^2+b^2+c^2+2ab+2bc+2ac-\dfrac{1}{4}\left(2a^2+2b^2+2c^2-2ab-2ac-2bc\right)\ge3ab+3bc+3ca\\ \Leftrightarrow a^2+b^2+c^2+2ab+2bc+2ac-\dfrac{1}{2}a^2-\dfrac{1}{2}b^2-\dfrac{1}{2}c^2-ab-bc-ac\ge0\\ \Leftrightarrow\dfrac{1}{2}a^2+\dfrac{1}{2}b^2+\dfrac{1}{2}c^2+ab+ac+bc\ge0\\ \Leftrightarrow a^2+b^2+c^2+2ab+2bc+2ac\ge0\\ \Leftrightarrow\left(a+b+c\right)^2\ge0\left(luôn.đúng\right)\)
Dấu \("="\Leftrightarrow a+b+c=0\)
\(1,a^2+b^2+c^2\ge ab+bc+ca\\ \Leftrightarrow2a^2+2b^2+2c^2-2ab-2ac-2bc\ge0\\ \Leftrightarrow\left(a^2-2ab+b^2\right)+\left(b^2-2bc+c^2\right)+\left(c^2-2ac+a^2\right)\ge0\\ \Leftrightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\ge0\left(luôn.đúng\right)\)
Dấu \("="\Leftrightarrow a=b=c\)
\(2,a^2+b^2+c^2+3\ge2\left(a+b+c\right)\\ \Leftrightarrow\left(a^2-2a+1\right)+\left(b^2-2b+1\right)+\left(c^2-2c+1\right)\ge0\\ \Leftrightarrow\left(a-1\right)^2+\left(b-1\right)^2+\left(c-1\right)^2\ge0\left(luôn.đúng\right)\)
Dấu \("="\Leftrightarrow a=b=c=1\)
\(3,\Leftrightarrow\dfrac{a^2+b^2+c^2}{3}\ge\dfrac{\left(a+b+c\right)^2}{9}\\ \Leftrightarrow9\left(a^2+b^2+c^2\right)\ge3\left(a+b+c\right)^2\\ \Leftrightarrow3\left(a^2+b^2+c^2\right)\ge\left(a+b+c\right)^2\\ \Leftrightarrow3a^2+3b^2+3c^2-a^2-b^2-c^2-2ab-2ac-2bc\ge0\\ \Leftrightarrow2a^2+2b^2+2c^2-2ab-2ac-2bc\ge0\left(luôn.đúng.do.câu.1\right)\)
Dấu \("="\Leftrightarrow a=b=c\)
\(4,\Leftrightarrow a^2b^2+b^2c^2+a^2c^2+2a^2bc+2ab^2c+2abc^2\ge3a^2bc+3ab^2c+3abc^2\\ \Leftrightarrow a^2b^2+b^2c^2+a^2c^2-a^2bc-ab^2c-abc^2\ge0\\ \Leftrightarrow2a^2b^2+2b^2c^2+2a^2c^2-2a^2bc-2ab^2c-2abc^2\ge0\\ \Leftrightarrow\left(a^2b^2-2a^2bc+a^2c^2\right)+\left(a^2b^2-2ab^2c+b^2c^2\right)+\left(b^2c^2-2abc^2+a^2c^2\right)\ge0\\ \Leftrightarrow\left(ab-ac\right)^2+\left(ab-bc\right)^2+\left(bc-ac\right)^2\ge0\left(luôn.đúng\right)\)
Dấu \("="\Leftrightarrow ab=bc=ac\)

* Khó khăn:
- Lực lượng chưa lớn mạnh.
- Nhà Minh áp đặt được bộ máy cai trị lâu dài.
- Quân Minh vây quét và tấn công:
+ Năm 1418, quân Minh đã tấn công căn cứ ở vùng núi Chi Linh. Lê Lai đã liều minh cứu chúa (Lê Lợi).
+ Cuối năm 1421, quân Minh thực hiện cuộc tấn công vào căn cứ của nghĩa quân => Nghĩa quân buộc phải rút lui lên núi Chí Linh.
+ Năm 1423, Lê Lợi chủ động hòa hoãn với quân Minh.
+ Năm 1424, quân Minh tấn công => Cuộc khởi nghĩa Lam Sơn chuyển sang giai đoạn mới.
mn ơi ai thấy bài này giúp em được ko ạ,e đang cần gấp lắm
a, Vì D,M là trung điểm AB,AC nên DM là đtb tg ABC
Do đó \(DM=\dfrac{1}{2}BC=\dfrac{7}{2}\left(cm\right)\) và DM//BC
Mọi người ơi giúp e vs bài 3 khó quá ạ 🥺