\(10,\\ a^2+b^2+c^2+d^2+e^2\ge a\left(b+c+d+e\right)\\ \Leftrightarrow4a^2+4b^2+4c^2+4d^2+4e^2\ge4ab+4ac+4ad+4ae\\ \Leftrightarrow\left(a^2-4ab+4b^2\right)+\left(a^2-4ac+4c^2\right)+\left(a^2-4ad+4d^2\right)+\left(a^2-4ae+4e^2\right)\ge0\\ \Leftrightarrow\left(a-2b\right)^2+\left(a-2c\right)^2+\left(a-2d\right)^2+\left(a-2e\right)^2\ge0\left(luôn.đúng\right)\)
Dấu \("="\Leftrightarrow\dfrac{a}{2}=b=c=d=e\)
\(4,\Leftrightarrow a^2+b^2+c^2+2ab+2bc+2ac-\dfrac{1}{4}\left(2a^2+2b^2+2c^2-2ab-2ac-2bc\right)\ge3ab+3bc+3ca\\ \Leftrightarrow a^2+b^2+c^2+2ab+2bc+2ac-\dfrac{1}{2}a^2-\dfrac{1}{2}b^2-\dfrac{1}{2}c^2-ab-bc-ac\ge0\\ \Leftrightarrow\dfrac{1}{2}a^2+\dfrac{1}{2}b^2+\dfrac{1}{2}c^2+ab+ac+bc\ge0\\ \Leftrightarrow a^2+b^2+c^2+2ab+2bc+2ac\ge0\\ \Leftrightarrow\left(a+b+c\right)^2\ge0\left(luôn.đúng\right)\)
Dấu \("="\Leftrightarrow a+b+c=0\)
\(1,a^2+b^2+c^2\ge ab+bc+ca\\ \Leftrightarrow2a^2+2b^2+2c^2-2ab-2ac-2bc\ge0\\ \Leftrightarrow\left(a^2-2ab+b^2\right)+\left(b^2-2bc+c^2\right)+\left(c^2-2ac+a^2\right)\ge0\\ \Leftrightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\ge0\left(luôn.đúng\right)\)
Dấu \("="\Leftrightarrow a=b=c\)
\(2,a^2+b^2+c^2+3\ge2\left(a+b+c\right)\\ \Leftrightarrow\left(a^2-2a+1\right)+\left(b^2-2b+1\right)+\left(c^2-2c+1\right)\ge0\\ \Leftrightarrow\left(a-1\right)^2+\left(b-1\right)^2+\left(c-1\right)^2\ge0\left(luôn.đúng\right)\)
Dấu \("="\Leftrightarrow a=b=c=1\)
\(3,\Leftrightarrow\dfrac{a^2+b^2+c^2}{3}\ge\dfrac{\left(a+b+c\right)^2}{9}\\ \Leftrightarrow9\left(a^2+b^2+c^2\right)\ge3\left(a+b+c\right)^2\\ \Leftrightarrow3\left(a^2+b^2+c^2\right)\ge\left(a+b+c\right)^2\\ \Leftrightarrow3a^2+3b^2+3c^2-a^2-b^2-c^2-2ab-2ac-2bc\ge0\\ \Leftrightarrow2a^2+2b^2+2c^2-2ab-2ac-2bc\ge0\left(luôn.đúng.do.câu.1\right)\)
Dấu \("="\Leftrightarrow a=b=c\)
\(4,\Leftrightarrow a^2b^2+b^2c^2+a^2c^2+2a^2bc+2ab^2c+2abc^2\ge3a^2bc+3ab^2c+3abc^2\\ \Leftrightarrow a^2b^2+b^2c^2+a^2c^2-a^2bc-ab^2c-abc^2\ge0\\ \Leftrightarrow2a^2b^2+2b^2c^2+2a^2c^2-2a^2bc-2ab^2c-2abc^2\ge0\\ \Leftrightarrow\left(a^2b^2-2a^2bc+a^2c^2\right)+\left(a^2b^2-2ab^2c+b^2c^2\right)+\left(b^2c^2-2abc^2+a^2c^2\right)\ge0\\ \Leftrightarrow\left(ab-ac\right)^2+\left(ab-bc\right)^2+\left(bc-ac\right)^2\ge0\left(luôn.đúng\right)\)
Dấu \("="\Leftrightarrow ab=bc=ac\)
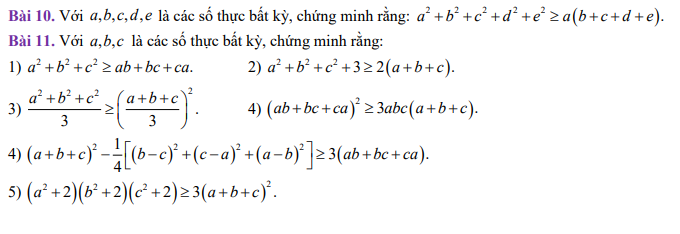
ai giúp em với ạ :3 e cảm ơn m.ng trước !! thân ái
