tìm x biết :x (x-2)-(x+5):(x-1)=23
tìm x biết :x (x-2)-(x+5):(x-1)=23
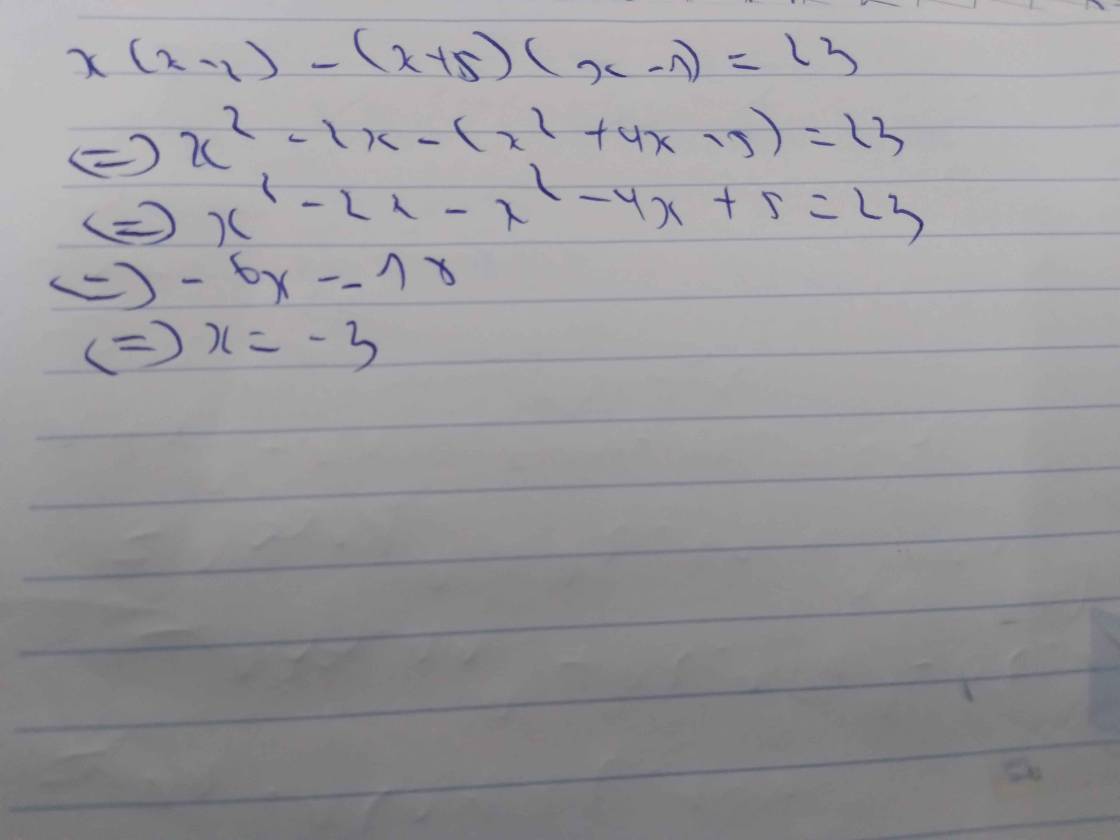 cái này cho phép mình sửa đề chỗ chia x-1 thành nhân x-1 nha
cái này cho phép mình sửa đề chỗ chia x-1 thành nhân x-1 nha
\(A=2xy+\dfrac{1}{2}x\left(2x-4xy+4\right)-x\left(x+2\right)\\ =2xy+x^2-2xy+2x-x^2-2x\\ =\left(2xy-2xy\right)+\left(x^2-x^2\right)+\left(2x-2x\right)=0\)
Vậy GT biểu thwusc A không phụ thuộc vào giá trị của biến
\(B=\left(2x-1\right)\left(2x+1\right)-\left(2x-3\right)^2-12\\ =\left[\left(2x\right)^2-1^2\right]-\left[\left(2x\right)^2-2.2x.3+3^2\right]-12\\ =4x^2-1-\left(4x^2-12x+9\right)-12\\ =\left(4x^2-4x^2\right)+12x+\left(-9-1-12\right)\\ =12x^2-22\)
Vậy biểu thức B có phụ thuộc vào giá trị biến
a: =2xy+1/2x*2x-1/2x*4y+1/2x*4-x^2-2x
=2xy-x^2+2x+x^2-2xy+2x
=0
b: \(=4x^2-1-12-\left(4x^2-12x+9\right)\)
=4x^2-13-4x^2+12x-9
=12x-22
c: \(=x^3+6x^2+12x+8-\left(x^3-9x^2+27x-27\right)-10x\)
=x^3+6x^2+2x+8-x^3+9x^2-27x+27
=15x^2-25x+35
d: \(=x^3-3x^2+3x-1-x\left(x^2-4\right)-\left(x^3+x^2+x+2x^2+2x+2\right)\)
\(=x^3-3x^2+3x-1-x^3+4x-\left(x^3+3x^2+3x+2\right)\)
\(=-3x^2+7x-1-x^3-3x^2-3x-2\)
=-x^3-6x^2+4x-3
Rút gọn
a. (3x3y2 - 9x2y2 + 15xy3) : 3xy2
\(\left(3x^3y^2-9x^2y^2+15xy^3\right):3xy^2\)
\(=3x^3y^2:3xy^2-9x^2y^2:3xy^2+15xy^3:3xy^2\)
\(=\left(3:3\right)\cdot x^{3-1}\cdot y^{2-2}-\left(9:3\right)\cdot x^{2-1}\cdot y^{2-2}+\left(15:3\right)\cdot x^{1-1}\cdot y^{3-2}\)
\(=x^2-3x+5y\)
Phân tích đa thúc thành nhân tử:
1,4x^2-4xy-y^2+25
\(1)\) \(-4x^2-4xy-y^2+25\) (sửa đề)
\(=25-\left(4x^2+4xy+y^2\right)\)
\(=5^2-\left(2x+y\right)^2\)
\(=\left(5-2x-y\right)\left(5+2x+y\right)\)
#Ayumu
Dùng tính chất cơ bản của phân thức, hãy giải thích vì sao có thể viết:
a, 2/6x= 4/12x
b, 3x+y/y= 3xy/y^2/y^2
- Giúp mình với ạ, mai mình thi rồi-
a: \(\dfrac{2}{6x}=\dfrac{2\cdot2}{6x\cdot2}=\dfrac{4}{12x}\)
b: \(\dfrac{3x+y}{y}=\dfrac{y\left(3x+y\right)}{y\cdot y}=\dfrac{3xy+y^2}{y^2}\)
Cho a,b,c là số thực,a+b+c=3,d+e+f=3.ad+be+cf=3.Cmr a+b+c+d+e+f
a.
\(P=\left(21x^4y^5\right):\left(7x^3y^3\right)=3xy^2\)
Tại \(x=-0,5;y=-2\Rightarrow P=3.\left(-0,5\right).\left(-2\right)^2=-6\)
b.
\(A=-2y+2x^3+8y-35-x^3=x^3+6y-35\)
Tại \(x=3;y=-4\Rightarrow A=3^3+6.\left(-4\right)-35=-32\)
c.
Đặt \(B=3x^2-4y+4x-3y^2=3\left(x^2-y^2\right)+4\left(x-y\right)\)
\(=3\left(x-y\right)\left(x+y\right)+4\left(x-y\right)=\left(x-y\right)\left[3\left(x+y\right)+4\right]\)
Tại \(x=-1;y=10\Rightarrow B=\left(-1-10\right)\left[3\left(-1+10\right)+4\right]=-341\)
d.
Đặt \(C=\dfrac{x^2-4x+4}{x-2}=\dfrac{\left(x-2\right)^2}{x-2}=x-2\)
Khi \(x=2020\Rightarrow C=2020-2=2018\)
e.
Đặt \(D=4x^2y+xy^2+5x^2y-xy^2=9x^2y\)
Tại \(x=-2;y=\dfrac{1}{2}\Rightarrow D=9.\left(-2\right)^2.\dfrac{1}{2}=18\)
1,
B=(1-2 trên x+1):(1-x^2-2 trên x^2-1)
C=9
Cho a,b,c là số thực,a+b+c=3,d+e+f=3.ad+be+cf=3.Cmr a+b+c+d+e+f
tìm x biết (x-1)^2=(2x+14)^2
\(\left(x-1\right)^2=\left(2x+14\right)^2\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=2x+14\\x-1=-\left(2x+14\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-x=-1-14\\x-1=-2x-14\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-15\\x+2x=-14+1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-15\\3x=-13\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-15\\x=-\dfrac{13}{3}\end{matrix}\right.\)
Vậy: \(S=\left\{-15;-\dfrac{13}{3}\right\}\)