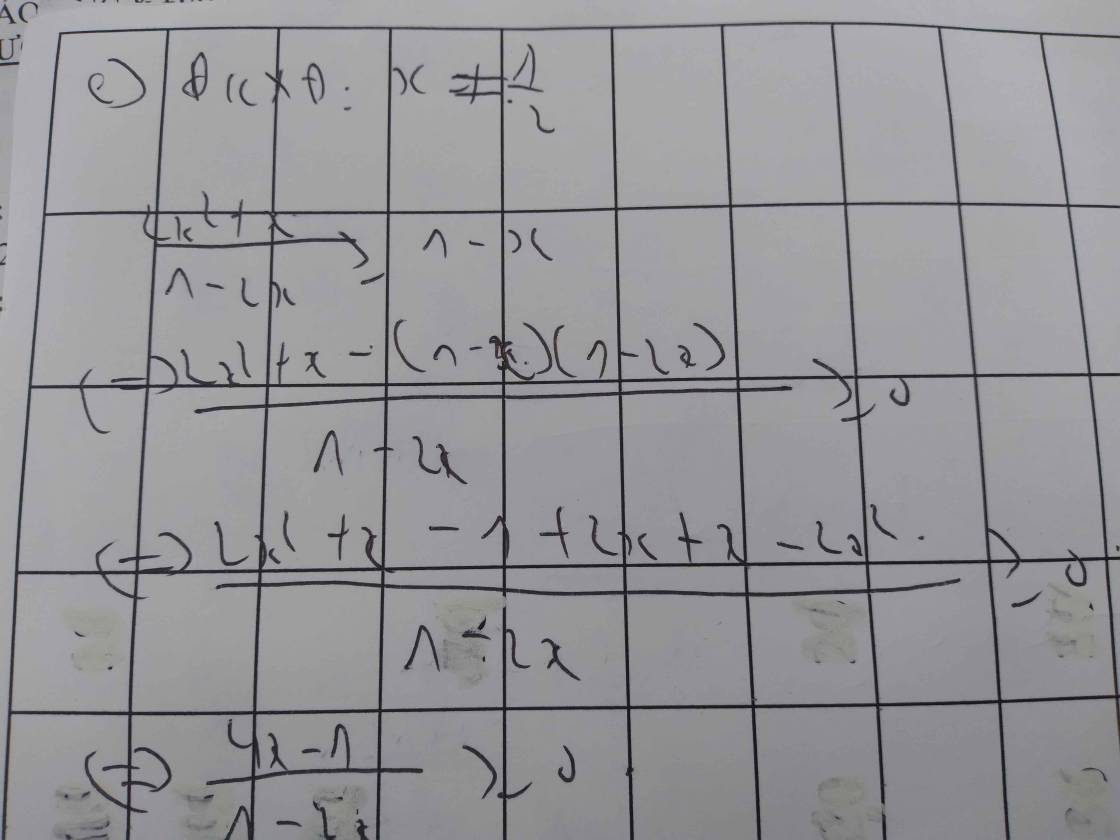
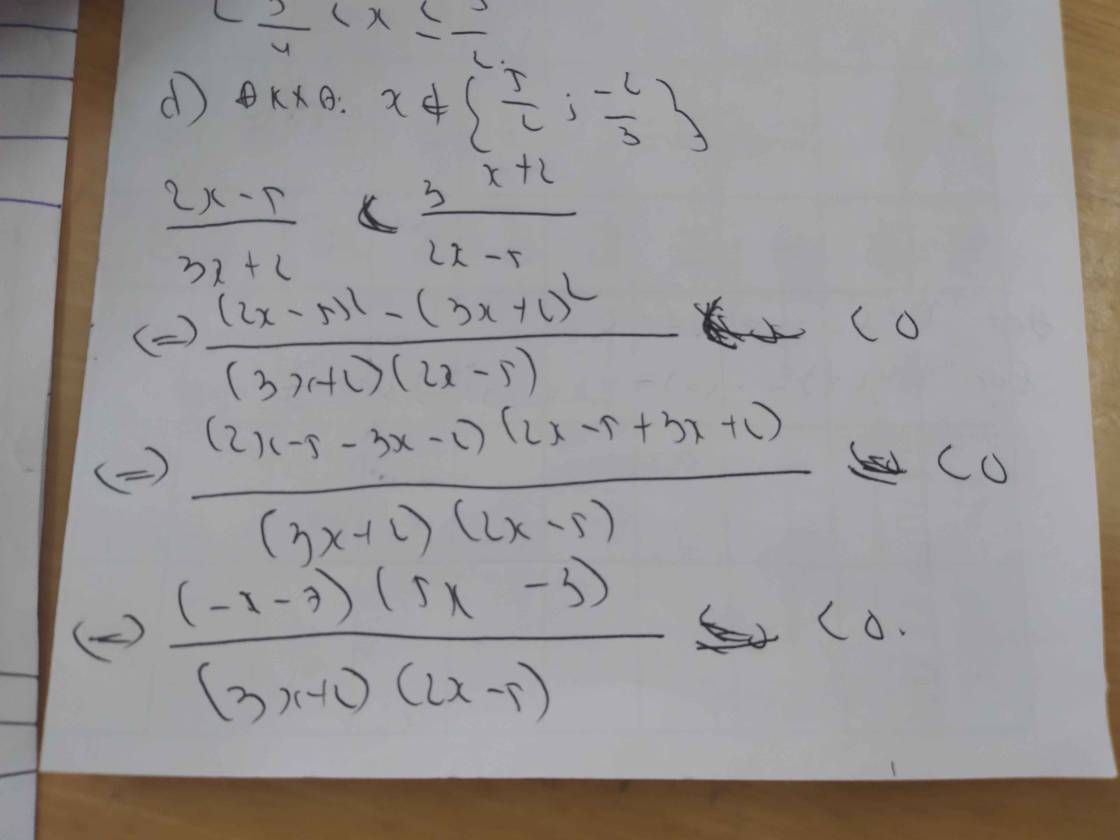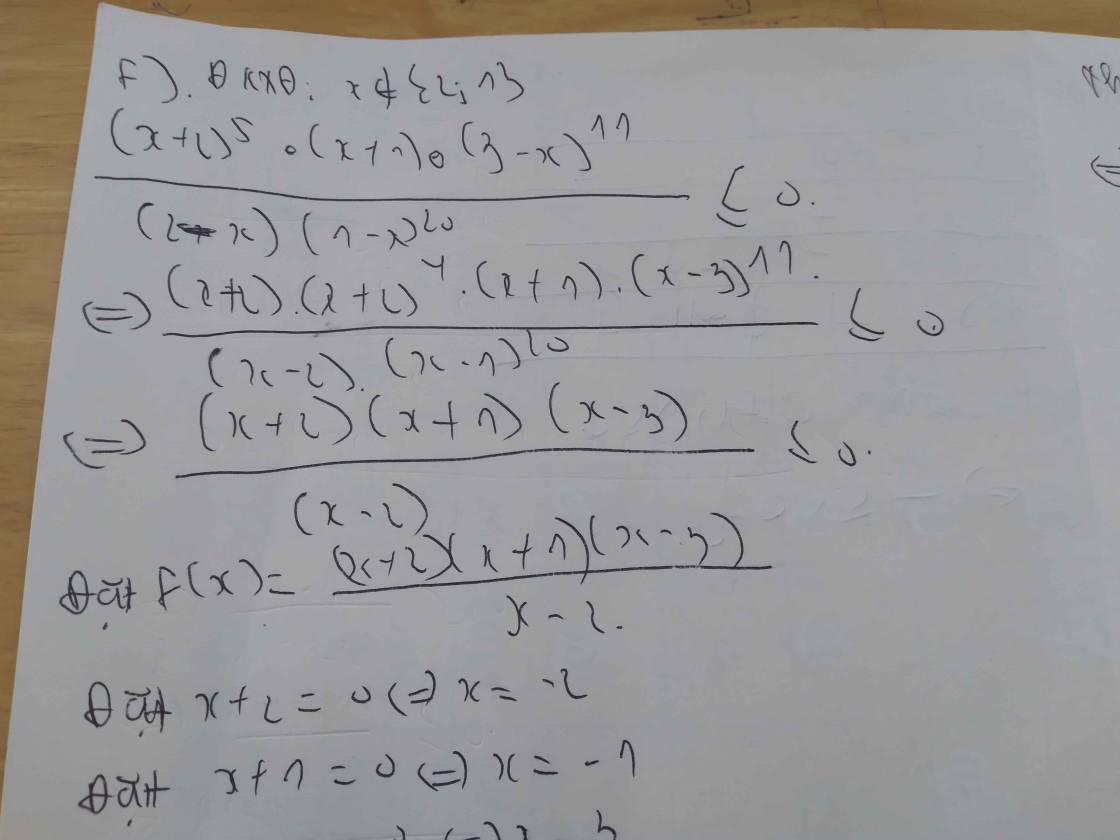\(\dfrac{2x+x^2+1}{x^2+1}\le0\)

Những câu hỏi liên quan
giải bpt
a. \(x^2-3x+2\le0\)
b.\(x^4-3x^2+2\le0\)
c.\(\dfrac{1}{x^2-x+1}\le\dfrac{1}{2x^2+x+2}\)
a: =>(x-1)(x-2)<=0
=>1<=x<=2
b: =>(x^2-1)(x^2-2)<=0
=>1<=x^2<=2
=>\(\left[{}\begin{matrix}1< =x< =\sqrt{2}\\-1>=x>=-\sqrt{2}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Giải các bất phương trình saua/ (x+1).(x-1).(3x-6)0b/ dfrac{x+3}{x-2}le0c/ dfrac{left(2x-5right).left(x+2right)}{-4x+3}ge0d/ dfrac{2x-5}{3x+2} dfrac{3x+2}{2x-5}e/ dfrac{2x^2+x}{1-2x}ge1-xf/ dfrac{left(2+xright)^5.left(x+1right).left(3-xright)^{11}}{left(2-xright).left(1-xright)^{20}}le0
Đọc tiếp
Giải các bất phương trình sau
a/ (x+1).(x-1).(3x-6)>0
b/ \(\dfrac{x+3}{x-2}\le0\)
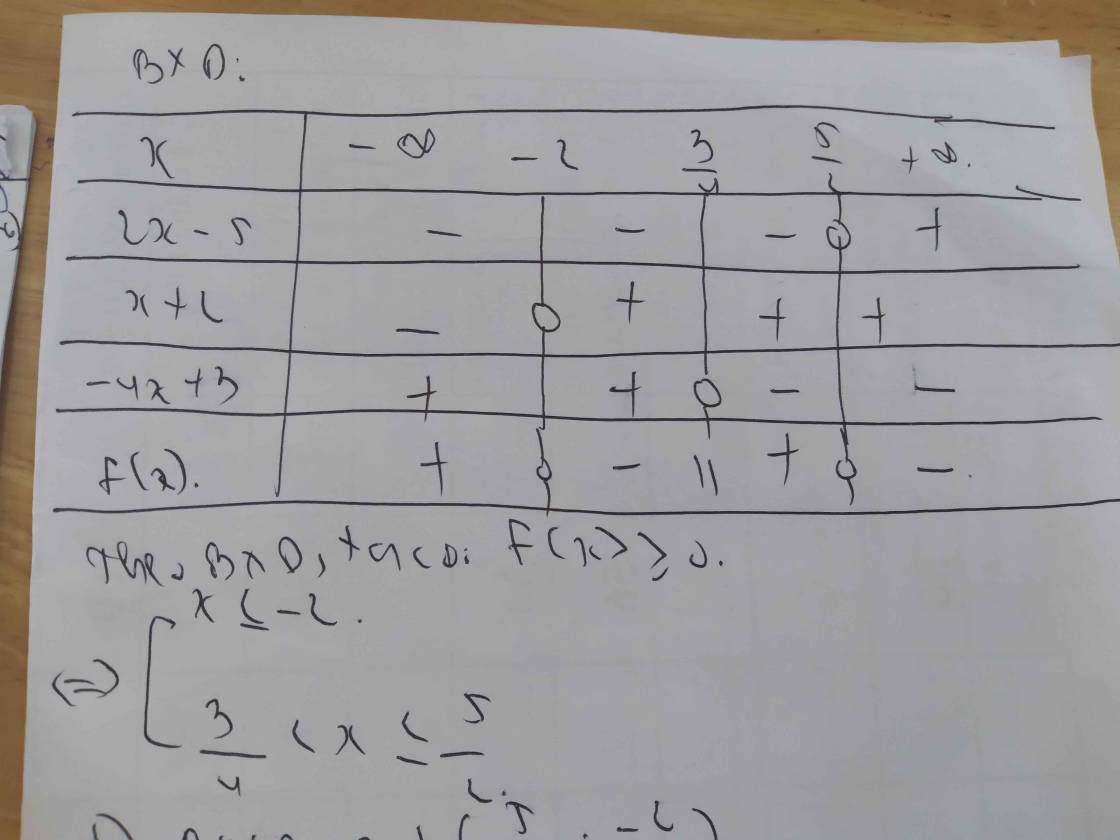
c/ \(\dfrac{\left(2x-5\right).\left(x+2\right)}{-4x+3}\ge0\)
d/ \(\dfrac{2x-5}{3x+2}< \dfrac{3x+2}{2x-5}\)
e/ \(\dfrac{2x^2+x}{1-2x}\ge1-x\)
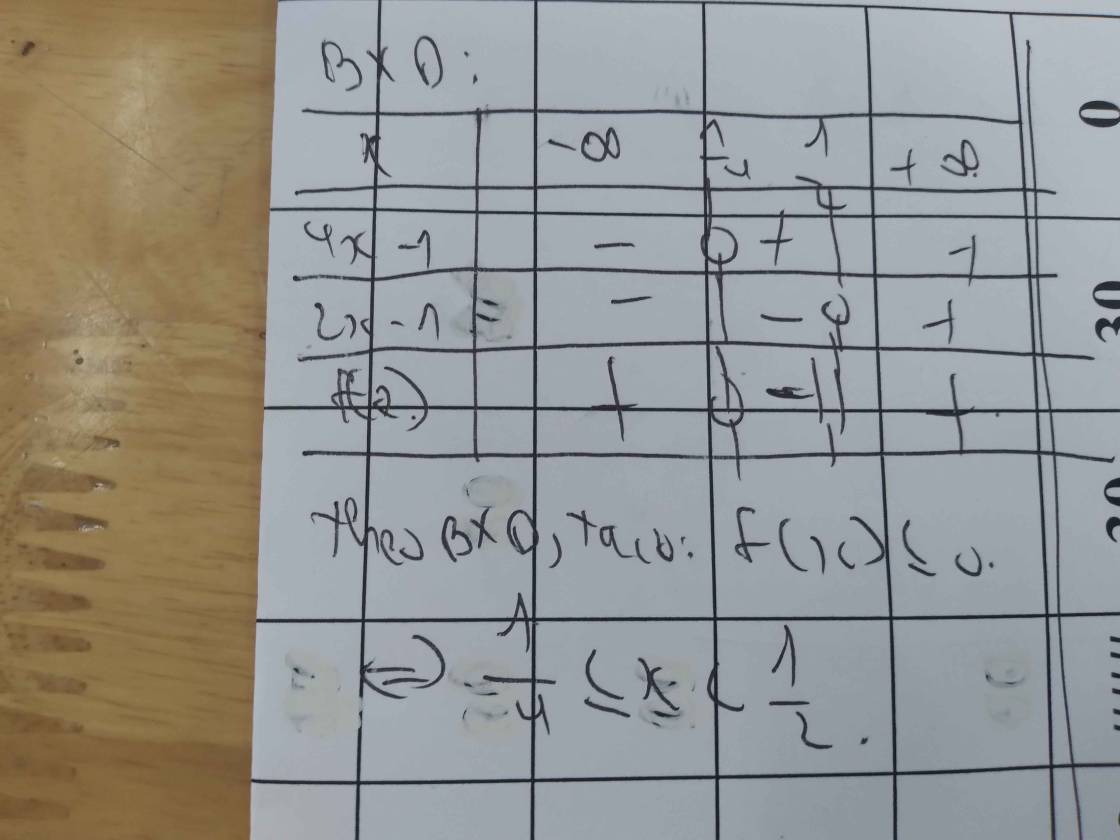
f/ \(\dfrac{\left(2+x\right)^5.\left(x+1\right).\left(3-x\right)^{11}}{\left(2-x\right).\left(1-x\right)^{20}}\le0\)
a) \(\left(x+1\right)\left(x-1\right)\left(3x-6\right)>0\)
Lập bảng xét dấu ta được kết quả :
\(Bpt\Leftrightarrow\left[{}\begin{matrix}-1< x< 1\\x>2\end{matrix}\right.\)
b) \(\dfrac{x+3}{x-2}\le0\)
Lập bảng xét dấu ta được kết quả :
\(Bpt\Leftrightarrow-3\le x< 2\)
d) \(\dfrac{2x-5}{3x+2}< \dfrac{3x+2}{2x-5}\)
\(\Leftrightarrow\dfrac{2x-5}{3x+2}-\dfrac{3x+2}{2x-5}< 0\)
\(\Leftrightarrow\dfrac{\left(2x-5\right)^2-\left(3x+2\right)^2}{\left(3x+2\right)\left(2x-5\right)}< 0\)
\(\Leftrightarrow\dfrac{\left(2x-5+3x+2\right)\left(2x-5-3x-2\right)}{\left(3x+2\right)\left(2x-5\right)}< 0\)
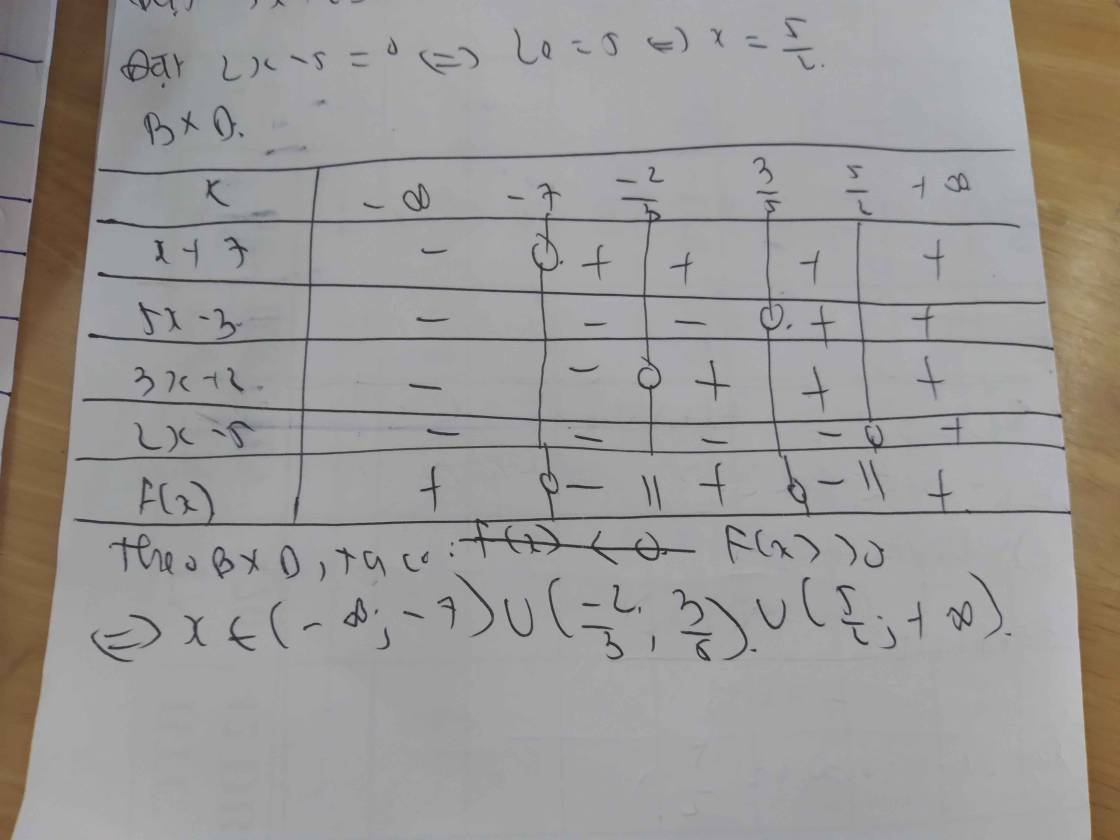
\(\Leftrightarrow\dfrac{-\left(5x-3\right)\left(x+7\right)}{\left(3x+2\right)\left(2x-5\right)}< 0\)
Lập bảng xét dấu ta được kết quả :
\(Bpt\Leftrightarrow\left[{}\begin{matrix}-7< x< -\dfrac{2}{3}\\\dfrac{5}{3}< x< \dfrac{5}{2}\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Giải các bất phương trình saua/ (x+1).(x-1).(3x-6)0b/ dfrac{x+3}{x-2}le0c/ dfrac{left(2x-5right).left(x+2right)}{-4x+3}ge0d/ dfrac{2x-5}{3x+2} dfrac{3x+2}{2x-5}e/ dfrac{2x^2+x}{1-2x}ge1-xf/ dfrac{left(2+xright)^5.left(x+1right).left(3-xright)^{11}}{left(2-xright).left(1-xright)^{20}}le0
Đọc tiếp
Giải các bất phương trình sau
a/ (x+1).(x-1).(3x-6)>0
b/ \(\dfrac{x+3}{x-2}\le0\)
c/ \(\dfrac{\left(2x-5\right).\left(x+2\right)}{-4x+3}\ge0\)
d/ \(\dfrac{2x-5}{3x+2}< \dfrac{3x+2}{2x-5}\)
e/ \(\dfrac{2x^2+x}{1-2x}\ge1-x\)
f/ \(\dfrac{\left(2+x\right)^5.\left(x+1\right).\left(3-x\right)^{11}}{\left(2-x\right).\left(1-x\right)^{20}}\le0\)
Tập nghiệm của bất phương trình \(\dfrac{2x\left(x^2-1\right)}{3-2x-x^2}\le0\) là
Tập nghiệm của BPT là: \(\left[{}\begin{matrix}-3< x\le-1\\0\le x< 1\\x>1\end{matrix}\right.\)
Đúng 1
Bình luận (0)
giúp mình giải bpt vs
\(\dfrac{\left|2x-1\right|-x}{2x}>1;\dfrac{2-\left|x-2\right|}{x^2-1}\ge0;\dfrac{\sqrt{x+4}-2}{4-9x^2}\le0;\dfrac{x^2-2x-3}{\sqrt[3]{3x-1}+\sqrt[3]{4-5x}}\ge0;\)\(3x^2-10x+3\ge0;\left(\sqrt{2}-x\right)\left(x^2-2\right)\left(2x-4\right)< 0;\dfrac{1}{x+9}-\dfrac{1}{x}>\dfrac{1}{2};\dfrac{2}{1-2x}\le\dfrac{3}{x+1}\)
Giải các bất phương trình sau
1) \(\dfrac{\text{x - 2}}{x+1}-\dfrac{3}{x+2}>0\) 2) \(\dfrac{\text{x + 1}}{x+2}+\dfrac{x}{x-3}\le0\)
3) \(\dfrac{\text{x}^2+2x+5}{x+4}>x-3\) 4) \(\sqrt{\text{x^2}-3x+2}\ge3\)
\(\dfrac{x-2}{x+1}-\dfrac{3}{x+2}>0.\left(x\ne-1;-2\right).\\ \Leftrightarrow\dfrac{x^2-4-3x-3}{\left(x+1\right)\left(x+2\right)}>0.\\ \Leftrightarrow\dfrac{x^2-3x-7}{\left(x+1\right)\left(x+2\right)}>0.\)
Đặt \(f\left(x\right)=\dfrac{x^2-3x-7}{\left(x+1\right)\left(x+2\right)}>0.\)
Ta có: \(x^2-3x-7=0.\Rightarrow\left[{}\begin{matrix}x=\dfrac{3+\sqrt{37}}{2}.\\x=\dfrac{3-\sqrt{37}}{2}.\end{matrix}\right.\)
\(x+1=0.\Leftrightarrow x=-1.\\ x+2=0.\Leftrightarrow x=-2.\)
Bảng xét dấu:
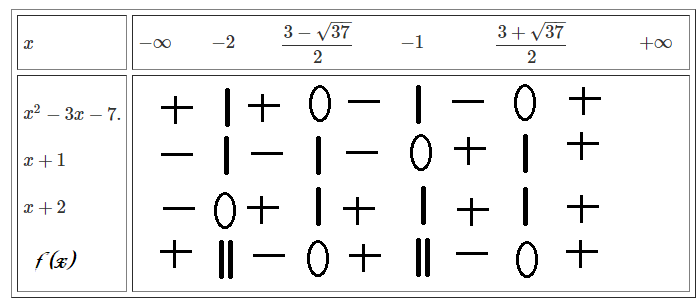
\(\Rightarrow f\left(x\right)>0\Leftrightarrow x\in\left(-\infty-2\right)\cup\left(\dfrac{3-\sqrt{37}}{2};-1\right)\cup\left(\dfrac{3+\sqrt{37}}{2};+\infty\right).\)
\(\sqrt{x^2-3x+2}\ge3.\\ \Leftrightarrow x^2-3x+2\ge9.\\ \Leftrightarrow x^2-3x-7\ge0.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{3-\sqrt{37}}{2}.\\x=\dfrac{3+\sqrt{37}}{2}.\end{matrix}\right.\)
Đặt \(f\left(x\right)=x^2-3x-7.\)
\(f\left(x\right)=x^2-3x-7.\)
\(\Rightarrow f\left(x\right)\ge0\Leftrightarrow x\in(-\infty;\dfrac{3-\sqrt{37}}{2}]\cup[\dfrac{3+\sqrt{37}}{2};+\infty).\)
\(\Rightarrow\sqrt{x^2-3x+2}\ge3\Leftrightarrow x\in(-\infty;\dfrac{3-\sqrt{37}}{2}]\cup[\dfrac{3+\sqrt{37}}{2};+\infty).\)
Đúng 1
Bình luận (0)
tìm TXĐ của hàm số:
y=\(\left\{{}\begin{matrix}\dfrac{2x-3}{x-1},x\le0\\-x^2+3x,x>0\end{matrix}\right.\)
Ta có \(-x^2+3x\) xác định với mọi \(x>0\)
\(x-1\ne0;\forall x\le0\Rightarrow\dfrac{2x-3}{x-1}\) xác định với mọi \(x\le0\)
\(\Rightarrow\) Hàm xác định với mọi x thuộc R hay \(D=R\)
Đúng 0
Bình luận (0)
Giải các BPT sau:
a) \(16x-5x^2-3\le0\)
b) \(\dfrac{2x+5}{x-24}>1\)
`a)16x-5x^2-3 <= 0`
`<=>5x^2-16x+3 >= 0`
`<=>5x^2-15x-x+3 >= 0`
`<=>(x-3)(5x-1) >= 0`
`<=>` $\left[\begin{matrix} \begin{cases} x-3 \ge 0<=>x \ge 3\\5x-1 \ge 0<=>x \ge \dfrac{1}{5} \end{cases}\\ \begin{cases} x-3 \le 0<=>x \le 3\\5x-1 \le 0<=>x \le \dfrac{1}{5} \end{cases}\end{matrix}\right.$
`<=>` $\left[\begin{matrix} x \ge 3\\ x \le \dfrac{1}{5}\end{matrix}\right.$
Vậy `S={x|x >= 3\text{ hoặc }x <= 1/5}`
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
`b)[2x+5]/[x-24] > 1`
`<=>[2x+5]/[x-24]-1 > 0`
`<=>[2x+5-x+24]/[x-24] > 0`
`<=>[x+29]/[x-24] > 0`
`<=>` $\left[\begin{matrix} x < -29 \\ x > 24\end{matrix}\right.$
Vậy `S={x|x > 24\text{ hoặc }x < -29}`
Đúng 2
Bình luận (0)
Tìm m để các hàm số f(x) = \(\left\{{}\begin{matrix}\dfrac{\sqrt{x+1}-1}{2x}khix>0\\2x^2+3mx+1khix\le0\end{matrix}\right.\) liên tục tại x=0
Lời giải:
Để hàm liên tục tại $x=0$ thì:
\(\lim\limits_{x\to 0+}f(x)=\lim\limits_{x\to 0-}f(x)=f(0)\)
\(\Leftrightarrow \lim\limits_{x\to 0+}\frac{\sqrt{x+1}-1}{2x}=\lim\limits_{x\to 0-}(2x^2+3mx+1)=1\)
\(\Leftrightarrow \lim\limits_{x\to 0+}\frac{1}{2(\sqrt{x+1}+1)}=0\Leftrightarrow \frac{1}{2}=0\) (vô lý)
Vậy không tồn tại $m$ thỏa mãn.
Đúng 0
Bình luận (0)