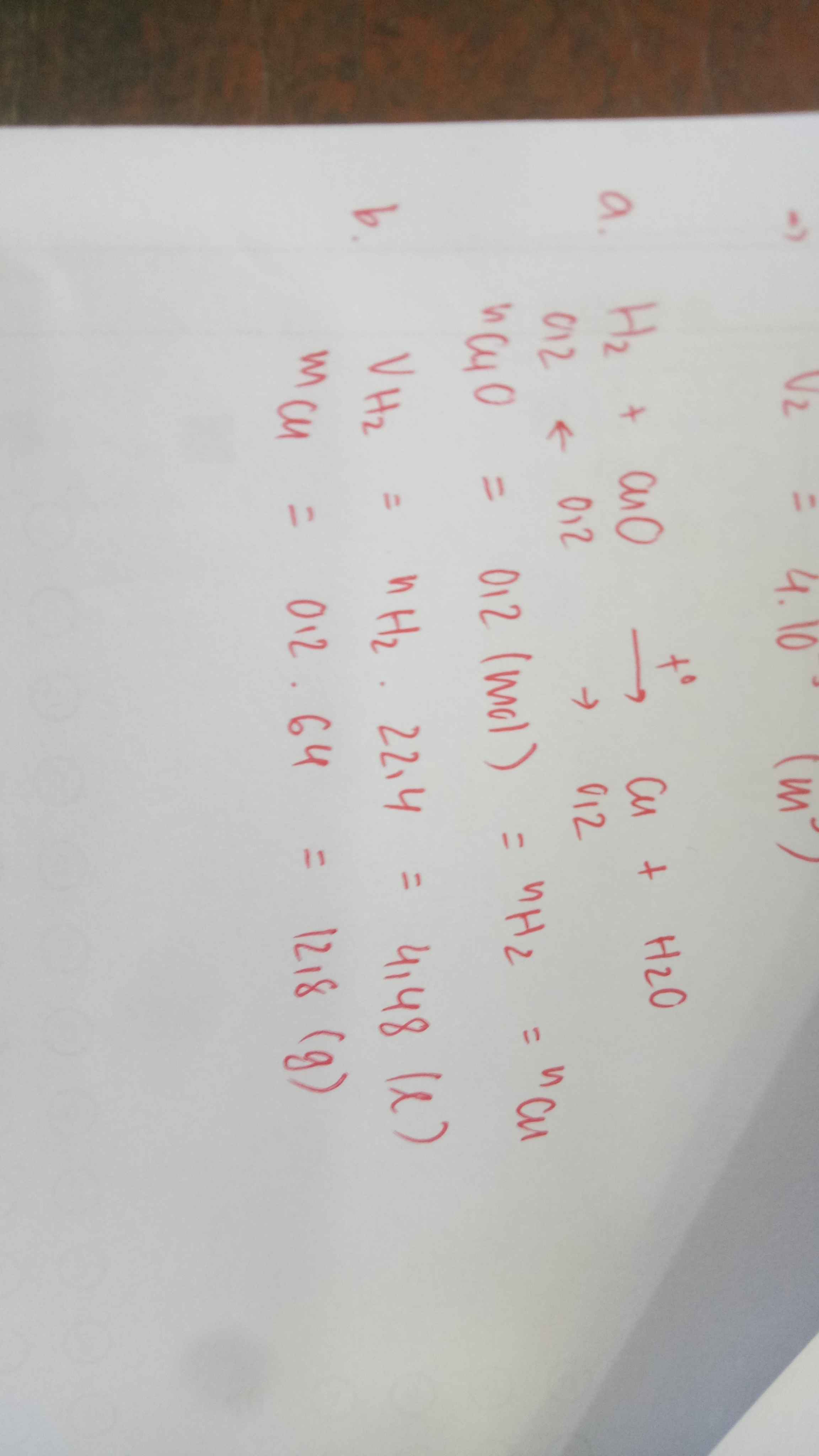BẠN VÀO CÂU HỎI TƯƠNG TỰ NHÉ

đây đâu phải là toán

\(\sqrt{10-2\sqrt{21}}+\sqrt{10+2\sqrt{21}}\)

\(=\sqrt{7-2\sqrt{21}+3}+\sqrt{7+2\sqrt{21}+3}\)

\(=\sqrt{\left(\sqrt{7}\right)^2-2.\sqrt{7}.\sqrt{3}+\left(\sqrt{3}\right)^2}+\sqrt{\left(\sqrt{7}\right)^2+2.\sqrt{7}.\sqrt{3}+\left(\sqrt{3}\right)^2}\)

\(=\sqrt{\left(\sqrt{7}-\sqrt{3}\right)^2}+\sqrt{\left(\sqrt{7}+\sqrt{3}\right)^2}\)

\(=\left|\sqrt{7}-\sqrt{3}\right|+\left|\sqrt{7}+\sqrt{3}\right|\)

\(=\sqrt{7}-\sqrt{3}+\sqrt{7}+\sqrt{3}\)

\(=\sqrt{7}+\sqrt{7}=2\sqrt{7}\)

Ta có: \(\sqrt{10-2\sqrt{21}}+\sqrt{10+2\sqrt{21}}\)

\(=\sqrt{7}-\sqrt{3}+\sqrt{7}+\sqrt{3}\)

\(=2\sqrt{7}\)

đặt \(A=\sqrt{10-2\sqrt{21}}+\sqrt{10+2\sqrt{21}}\)

\(=>A^2=10-2\sqrt{21}+10+2\sqrt{21}+2\sqrt{\left(10-2\sqrt{21}\right)\left(10+2\sqrt{21}\right)}\)

\(=>A^2=20+2\sqrt{10^2-\left(2\sqrt{21}\right)^2}=20+2\sqrt{16}=20+2.4=28\)

\(=>A=\sqrt{28}=2\sqrt{7}\)

Ta có :

​Vì 101¹⁰>99¹⁰\(\Leftrightarrow\)101¹⁰.99¹⁰>99¹⁰.99¹⁰\(\Leftrightarrow\)9999¹⁰>99²⁰

Vậy 9999¹⁰>99²⁰

99^20 < 9999^10

Câu hỏi tương tự nha bạn

( 2003 x 58 + 52 x 2003 - 10 x 2003 ) + ( 670 - 335 ) x 100

= 2003 x ( 58 + 52 -10 ) + 315 x 100

= 2003 x 100 + 315 x 100

= 200300 + 31500

= 231800

( 2003 x 58 + 52 x 2003 - 10 x 2003 ) + ( 670 - 355 ) x 100

= 200300      +  315   x100

=        200300   + 31500                    

=      231800

2003 x 58 + 52 x 2003 - 10 x 2003 ) + ( 670 - 335 ) x 100

= 2003 x ( 58 + 52 -10 ) + 315 x 100

= 2003 x 100 + 315 x 100

= 200300 + 31500

= 231800

315𝑥_¹⁰⁰+200300

( 2003 x 58 + 52 x 2003 - 10 x 2003 ) + ( 670 - 355 ) x 100

= 200300      +  315   x100

=        200300   + 31500                    

=      231800

( 2003 x 58 + 52 x 2003 - 10 x 2003 ) + ( 670 - 355 ) x 100

=  [2003 x ( 58 + 52 - 10 ] + 315 x 100

= ( 2003 x 100 ) + 315 x 100

= 200300 + 31500

= 231800

Ta có

 \(a^2+1=a^2+ab+bc+ca=a\left(a+b\right)+c\left(a+b\right)=\left(a+b\right).\left(a+c\right)\\ Cmtt:b^2+1=\left(b+a\right).\left(b+c\right)\\ c^2+1=\left(c+a\right).\left(c+b\right)\)

Nên

 \(\dfrac{b-c}{a^2+1}+\dfrac{c-a}{b^2+1}+\dfrac{a-b}{c^2+1}\\ =\dfrac{\left(b-c\right)}{\left(a+b\right)\left(a+c\right)}+\dfrac{\left(c-a\right)}{\left(b+c\right)\left(b+a\right)}+\dfrac{\left(a-b\right)}{\left(c+a\right)\left(c+b\right)}\\ =\dfrac{\left(b-c\right)\left(b+c\right)+\left(c-a\right)\left(c+a\right)+\left(a-b\right)\left(a+b\right)}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}\\ =\dfrac{b^2-c^2+c^2-a^2+a^2-b^2}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}\\ =0\)

\(\dfrac{b-c}{a^2+1}+\dfrac{c-a}{b^2+1}+\dfrac{a-b}{c^2+1}\)

\(=\dfrac{b-c}{a^2+ab+bc+ac}+\dfrac{c-a}{b^2+ab+bc+ca}+\dfrac{a-b}{c^2+ab+bc+ca}\)

\(=\dfrac{b-c}{a\left(a+b\right)+c\left(a+b\right)}+\dfrac{c-a}{b\left(a+b\right)+c\left(a+b\right)}+\dfrac{a-b}{c\left(c+a\right)+b\left(a+c\right)}\)

\(=\dfrac{b-c}{\left(a+c\right)\left(a+b\right)}+\dfrac{c-a}{\left(b+c\right)\left(a+b\right)}+\dfrac{a-b}{\left(b+c\right)\left(a+c\right)}\)

\(=\dfrac{\left(b-c\right)\left(b+c\right)+\left(c-a\right)\left(a+c\right)+\left(a-b\right)\left(a+b\right)}{\left(a+c\right)\left(a+b\right)\left(b+c\right)}\)

\(=\dfrac{b^2-c^2+c^2-a^2+a^2-b^2}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}=0\) 

?

giải j bn?

:)?

Kẻ OM vuông óc với CD 

Vì CD là 1 dây của (O)

=> M là trung điểm của CD 

=> MC = MD
Có: AH // BK (cùng vuông góc với CD)

=> AHKB là Hình thang

Lại có: OM vuông góc với CD; O là trung điểm của AB

=> M là trung điểm của HK

=> MH = MK

Có: \(\left\{{}\begin{matrix}HD+MD=HM\\MC+CK=MK\end{matrix}\right.\)

Mà: MH = MK (cmt) và MD = MC (cmt)

=> HD = CK