a) Cho \(a^m=a^n\left(a\in Q;m,n\in N\right)\)Tìm các số m,n
b) Cho \(a^m=a^n\left(a\in Q;\right)a>0;m,n\in N\)So sánh m,n
a) Cho phân số \(\frac{a}{b}\left(a,b\in N;b\ne0\right)\).
Biết \(\frac{a}{b}< 1\left(m\in N,m\ne0\right)\)
CM rằng:\(\frac{a}{b}< \frac{a+m}{b+m}\)
Ta có:
\(\frac{a}{b}< 1\\ \Rightarrow a< b\\ \Rightarrow am< bm\left(m\in N^{\cdot}\right)\\ \Rightarrow am+ab< bm+ab\\\Rightarrow a\left(b+m\right)< b\left(a+m\right)\\ \Rightarrow\frac{a}{b} < \frac{a+m}{b+m}\)
1, Tìm \(n\in N\)* để: \(A=2016n+3\) là lập phương của một số tự nhiên.
2, Tìm \(a,b,c\in N\)* sao cho: \(A=\dfrac{\left(ab-1\right)\left(bc-1\right)\left(ac-1\right)}{abc}\in Z\)
3, Tìm \(a,b,c\in Z\) biết:
\(\left|a-b\right|+\left|b-c\right|+\left|a-c\right|=2017^{2018}\)
Cho \(A=\left\{x\in N|11-3x>0\right\}\)
\(B=\left\{x\in Z|\left|x\right|\le3\right\}\)
a, Tìm \(A\cup B,A\cap B,C_BA,\) A \ B, B \ A.
b, Tìm X là tập các số nguyên thỏa mãn \(A\subset X\subset B\)
\(11-3x>0\Leftrightarrow x< \frac{11}{3}\Rightarrow A=\left\{0;1;2;3\right\}\)
\(B=\left\{-3;-2;-1;0;1;2;3\right\}\)
\(A\cup B=B=...\)
\(A\cap B=A=...\)
\(C_BA=\left\{-3;-2;-1\right\}\)
\(A\backslash B=\varnothing\)
\(B\backslash A=\left\{-3;-2;-1\right\}\)
\(X=A;\left\{-3;0;1;2;3\right\};\left\{-2;0;1;2;3\right\};\left\{-1;0;1;2;3\right\}\) ; \(\left\{-3;-2;0;1;2;3\right\};\left\{-3;-1;0;1;2;3\right\};\left\{-2;-1;0;1;2;3\right\};B\)
Cho A={\(x\in Z||x|\le\dfrac{10}{3}\)}
B=\(\left\{x\in R\left|\left(x^2-4\right)\times\left(16-x^2\right)\right|=0\right\}\)
1, Tìm \(A\cap B\)\(,A\cup B\)A-B,B-A
2, Tìm tất cả tập X thỏa mãn : \(X\in A\), \(X\in B\)
3, Tìm tập hợp Y thỏa mãn :\(Y\subset A,Y\cap B\ne\varnothing\)
4, Tìm số tập hợp D thỏa mãn : \(D\subset A,D\subseteq B\)
1: A={-3;-2;-1;0;1;2;3}
B={2;-2;4;-4}
A giao B={2;-2}
A hợp B={-3;-2;-1;0;1;2;3;4;-4}
2: x thuộc A giao B
=>\(x=\left\{2;-2\right\}\)
Cho \(A=\left\{3k+1|k\in N\right\};B=\left\{6m+1|m\in N\right\}\)
Hãy xác định tập hợp \(A\cap B;A\) \ B
Ta thấy 3k+1 là số chẵn, 6m+1 là số lẻ với \(k,m\ne0\). Với k=m=0: 3k+1=6m+1=1.
Vậy \(A\cap B=\left\{1\right\}\);A\B={3k+1|\(k\in\text{ℕ*}\)}
#Walker
Cho a,b,c \(\in\) Q thỏa mãn a.b+b.c+c.a =1
CM:\(\sqrt{\left(a^2+1\right).\left(b^2+1\right).\left(c^2+1\right)}\in Q\)
thay trực tiếp giả thiết ta có
\(\sqrt{\left(a^2+1\right)}=\sqrt{a^2+ab+bc+ac}=\sqrt{a\left(a+b\right)+c\left(a+b\right)}=\sqrt{\left(a+c\right)\left(a+b\right)}\)
tương tự ta có
\(\sqrt{b^2+1}=\sqrt{\left(b+a\right)\left(b+c\right)}\)
\(\sqrt{c^2+1}=\sqrt{\left(c+a\right)\left(c+b\right)}\)
nên
\(\sqrt{\left(a^2+1\right)\left(b^2+1\right)\left(c^2+1\right)}=\sqrt{\left(\left(a+b\right)\left(a+c\right)\left(b+c\right)\right)^2}=\left|\left(a+b\right)\left(a+c\right)\left(b+c\right)\right|\)
mà \(a,b,c\in Q\) nên \(\left|\left(a+b\right)\left(a+c\right)\left(b+c\right)\right|\in Q\Rightarrowđpcm\)
Có thể có phân số \(\dfrac{a}{b},\left(a,b\in\mathbb{Z},b\ne0\right)\) sao cho :
\(\dfrac{a}{b}=\dfrac{a.m}{b.n},\left(m,n\in\mathbb{Z};m,n\ne0,m\ne n\right)\) hay không ?
Có thể có phân số a/b (a, b ∈ Z, b ≠ 0) sao cho:
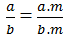
Vì 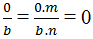
cho tập A = \(\left\{\frac{1}{6};\frac{1}{12};\frac{1}{30};...;\frac{1}{420}\right\}\) ta có thể viết lại tập A là?
A. A=\(\left\{\frac{1}{x\left(x-2\right)}|x\in Z;1\le x\le19\right\}\)
B. A= \(\left\{\frac{1}{x\left(x+1\right)}|x\in N;2\le x\le22\right\}\)
C. A=\(\left\{\frac{1}{x\left(x+2\right)}|x\in Z;1\le x\le20\right\}\)
D. A=\(\left\{\frac{1}{x\left(x+1\right)}|x\in N;2\le x\le20\right\}\)
bạn nào giúp mình chọn đáp án đúng và giải thích làm như nào hộ mk vs ạ. mình cảm ơn
Lời giải:
Tập A sửa lại thành \(A=\left\{\frac{1}{6};\frac{1}{12};\frac{1}{20}; \frac{1}{30};....;\frac{1}{420}\right\}\)
Ta thấy:
\(\frac{1}{6}=\frac{1}{2.3}\)
\(\frac{1}{12}=\frac{1}{3.4}\)
\(\frac{1}{20}=\frac{1}{4.5}\)
.....
\(\frac{1}{420}=\frac{1}{20.21}\)
Do đó công thức tổng quát của các phần tử thuộc tập A là \(\frac{1}{x(x+1)}|x\in \mathbb{N}; 2\leq x\leq 20\)
Đáp án D.
Bài 1:Cho A=\(\frac{4}{\left(n-2\right).\left(n+1\right)}\),\(n\in Z\)
a)Với \(n\in Z\)nào thì A không tồn tại
b)Viết tập hợp M các số nguyên n để A tồn tại
c) Tìm phân số A, biết n=2, n=0, n=11
d)Tìm \(n\in Z\) để A=\(\frac{1}{7}\)
a) 2 hoặc -1
b)M={-3;-2;0;1;3;4;5}