Sao suy ra được chỗ này vậy

Những câu hỏi liên quan
Tại sao chỗ này ra được 12 vậy???
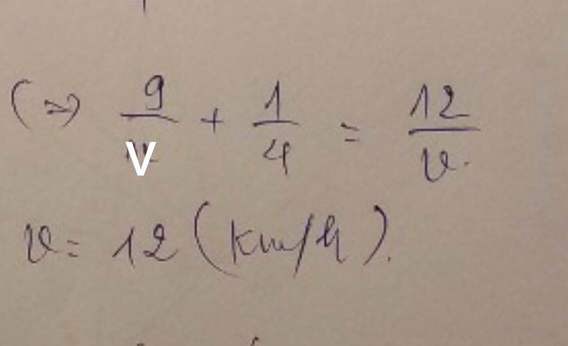
\(\dfrac{9}{v}+\dfrac{1}{4}=\dfrac{12}{v}\)
=> \(9+\dfrac{1}{4}v=12\)
=> \(v=\dfrac{12-9}{\dfrac{1}{4}}=12\left(km/h\right)\)
Đúng 4
Bình luận (0)
Mn ơi cho em hỏi từ chỗ dấu bằng số 2 làm sao suy ra mẫu chung đó được vậy ạ? E cám ơn ạ
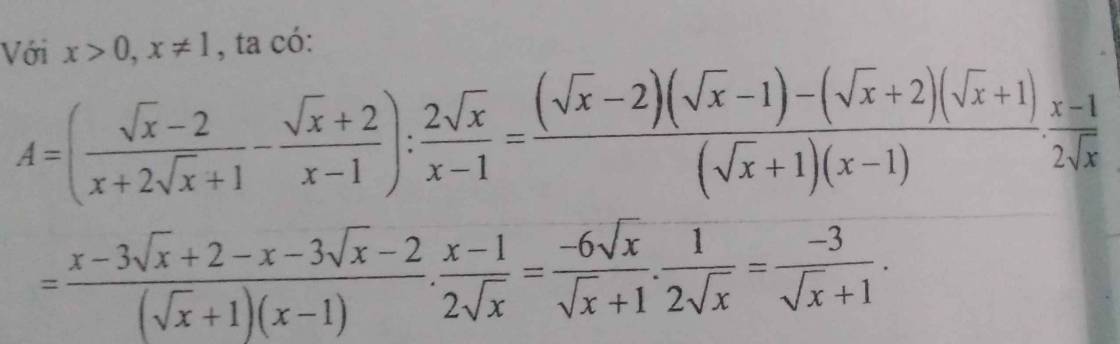
\(A=\left(\dfrac{\sqrt{x}-2}{x+2\sqrt{x}+1}-\dfrac{\sqrt{x}+2}{x-1}\right):\dfrac{2\sqrt{x}}{x-1}\)
\(=\left(\dfrac{\sqrt{x}-2}{\sqrt{x}^2+2\sqrt{x}+1^2}-\dfrac{\sqrt{x}+2}{\sqrt{x}^2-1^2}\right).\dfrac{x-1}{2\sqrt{x}}\)
\(=\left(\dfrac{\sqrt{x}-2}{\left(\sqrt{x}+1\right)^2}-\dfrac{\sqrt{x}+2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right).\dfrac{x-1}{2\sqrt{x}}\)
Tới đây là có được mẫu chung ở dấu = thứ 2 rồi.
Đúng 5
Bình luận (2)
\(A=\left(\dfrac{\sqrt{x}-2}{x+2\sqrt{x}+1}-\dfrac{\sqrt{x}+2}{x-1}\right):\dfrac{2\sqrt{x}}{x-1}\) ( với x>0;\(x\ne1\) )
\(=\left[\dfrac{\sqrt{x}-2}{\left(\sqrt{x}+1\right)^2}-\dfrac{\sqrt{x}+2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right].\dfrac{x-1}{2\sqrt{x}}\)
\(=\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)-\left(\sqrt{x}+2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)\left(x-1\right)}.\dfrac{x-1}{2\sqrt{x}}\)
\(=.....\) ( theo như trên )
Đúng 3
Bình luận (0)
Cái này là một phần bài giải mà em nhận được nhưng cái chỗ để ra x=0,2 và y=0,1 chỗ đó em ko biết làm sao để ra như vậy. Mọi người giải chi tiết chỗ đó dùm em ạ tại cô em bắt giải chi tiết ạ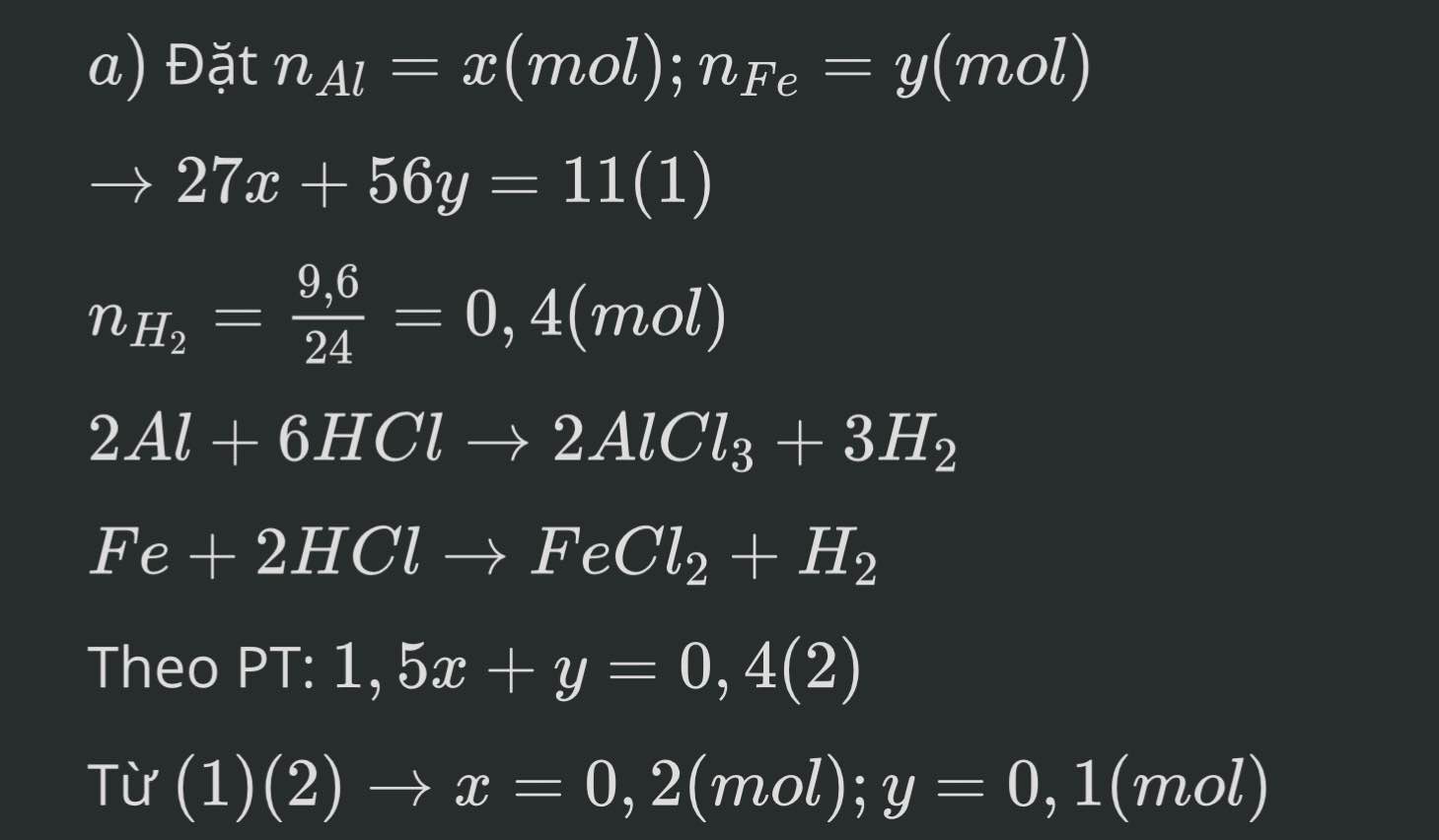
bạn bấm máy tính hoặc giải hệ:
\(\left\{{}\begin{matrix}27x+56y=11\\1,5x+y=0,4\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}27x+56y=11\\84x+56y=22,4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}57x=11,4\\27x+56y=11\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=0,2\\27.0,2+56y=11\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=0,2\\y=0,1\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Các Bạn không cần làm mà chỉ mình chỗ này mình chưa hiểu :
Phần B Khi mà giải ra B = 4/( 3 - căn x) thì làm sao để biết được (3 - căn x) này là âm ạ. Hay cả trên tử cũng vậy (1+căn x) 
\(3-\sqrt{x}\) chưa chắc đã âm
thử x=4=>3-2=1>0
Đúng 0
Bình luận (1)
mn ơi tại sao từ hàng trên suy ra hàng dưới được vậy ạaa
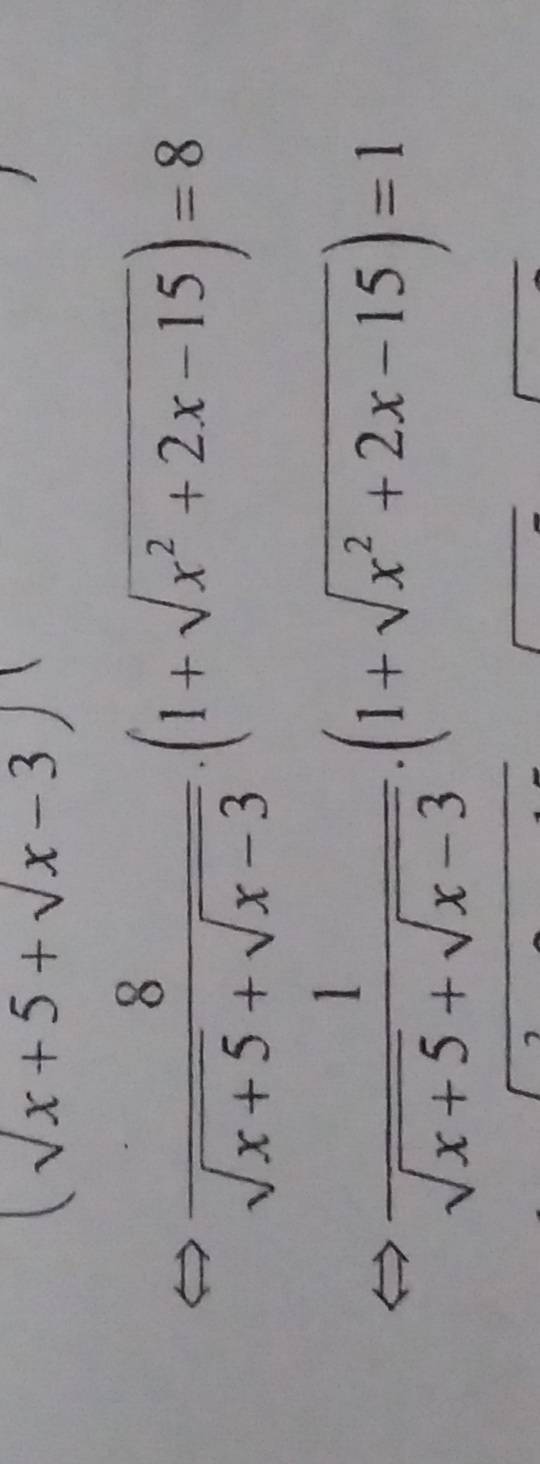
Các Bạn không cần làm mà chỉ mình chỗ này mình chưa hiểu : Phần B Khi mà giải ra B = 4/( 3 - căn x) thì làm sao để biết được (3 - căn x) này là âm ạ. Hay cả trên tử cũng vậy (1+căn x) ( liên quan tới hình ảnh bên dưới) 
cái này thì ko nhất thiết phải Cm nha bạn
Câu b kêu tìm x để B ko nhỏ hơn hoặc bằng A
Nghĩa là
\(\dfrac{4}{3-\sqrt{x}}>1\)
\(\Leftrightarrow\dfrac{4}{3-\sqrt{x}}-1>0\)
\(\Leftrightarrow\dfrac{4-\left(3-\sqrt{x}\right)}{3-\sqrt{x}}>0\)
\(\Leftrightarrow\dfrac{\sqrt{x}+1}{3-\sqrt{x}}>0\)
\(\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}\sqrt{x}+1>0\\3-\sqrt{x}>0\end{matrix}\right.\\\left\{{}\begin{matrix}\sqrt{x}+1< 0\left(VL\right)\\3-\sqrt{x}< 0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow3-\sqrt{x}>0\)
\(\Leftrightarrow\sqrt{x}< 3\)
\(\Leftrightarrow x< 9\)
Theo Đk ta có x≥0
Vậy 0≤x<9 thì B ko nhỏ hơn hoặc bằng A
Đúng 1
Bình luận (1)
Lời giải giống như bạn dưới đã viết.
Để $B$ không nhỏ hơn hoặc bằng $A$
Tức là $B>A$
$\Leftrightarrow \frac{4}{3-\sqrt{x}}>1$
$\Leftrightarrow \frac{4}{3-\sqrt{x}}-1>0\Leftrightarrow \frac{\sqrt{x}+1}{3-\sqrt{x}}>0$
Để phân thức này dương thì tử và mẫu phải cùng dấu.
Mà $\sqrt{x}+1\geq 0+1>0$ (dương rồi) nên $\sqrt{3}-x$ cũng dương.
------------------------
Đây là cách dễ làm nhất đối với bài này.
------------------------
Về phần lời giải của cô em, chị nghĩ trong lúc giảng em bị miss mất 1 số ý chứ ý cô không phải khẳng định mẫu âm đâu. Có lẽ ý của cô em thế này:
Khi em có: $\frac{4}{3-\sqrt{x}}>1$ thì em không nên nhân chéo mà nên trừ để đưa về hiệu >0 (như bạn Khoa đã giải). Nếu nhân chéo, em sẽ mắc phải 2 TH mẫu âm, mẫu dương như sau:
TH1: $3-\sqrt{x}>0$ thì $\frac{4}{3-\sqrt{x}}>1$ tương đương với $4> 3-\sqrt{x}$
TH2: $3-\sqrt{x}< 0$ thì tương đương $4< 3-\sqrt{x}$ (khi nhân 2 vế với số âm thì phải đổi dấu)
Như vậy thì rất là phức tạp. Nên để tránh TH mẫu âm mà hs giữ nguyên dấu khi nhân chéo thì cô em khuyên như vậy.
Đúng 0
Bình luận (0)
Em còn chỗ nào chưa hiểu thì cứ hỏi thoải mái.
Đúng 0
Bình luận (0)
Tại sao f'(t)>0 suy ra được mcosx-sinx=2(1-sinx) vậy ạ

Tính chất hàm đặc trưng
Nếu \(f\left(x\right)\) đơn điệu thì \(f\left(x_1\right)=f\left(x_2\right)\Leftrightarrow x_1=x_2\)
Ở đây \(f\left(t\right)=e^t+t\) đơn điệu nên \(f\left(t_1\right)=f\left(t_2\right)\Leftrightarrow t_1=t_2\)
Trong đó \(\left\{{}\begin{matrix}t_1=m.cosx-sinx\\t_2=2\left(1-sinx\right)\end{matrix}\right.\)
Đúng 3
Bình luận (0)
cho mình hỏi tại sao ra được chỗ màu đỏ vậy. mình cảm ơn nha


Mọi người ơi, giải thích giùm em chỗ này với ạ .Tại sao cos2x + 60 lại phân tích được sin(90 -(2x+ 6.....vậy ạ. Em cảm ơn
Đọc tiếp
Mọi người ơi, giải thích giùm em chỗ này với ạ .Tại sao cos2x + 60 lại phân tích được sin(90 -(2x\(+\) 6.....vậy ạ. Em cảm ơn
Sử dụng công thức: \(cos\alpha=sin\left(90^0-\alpha\right)\)
Đúng 1
Bình luận (0)





























