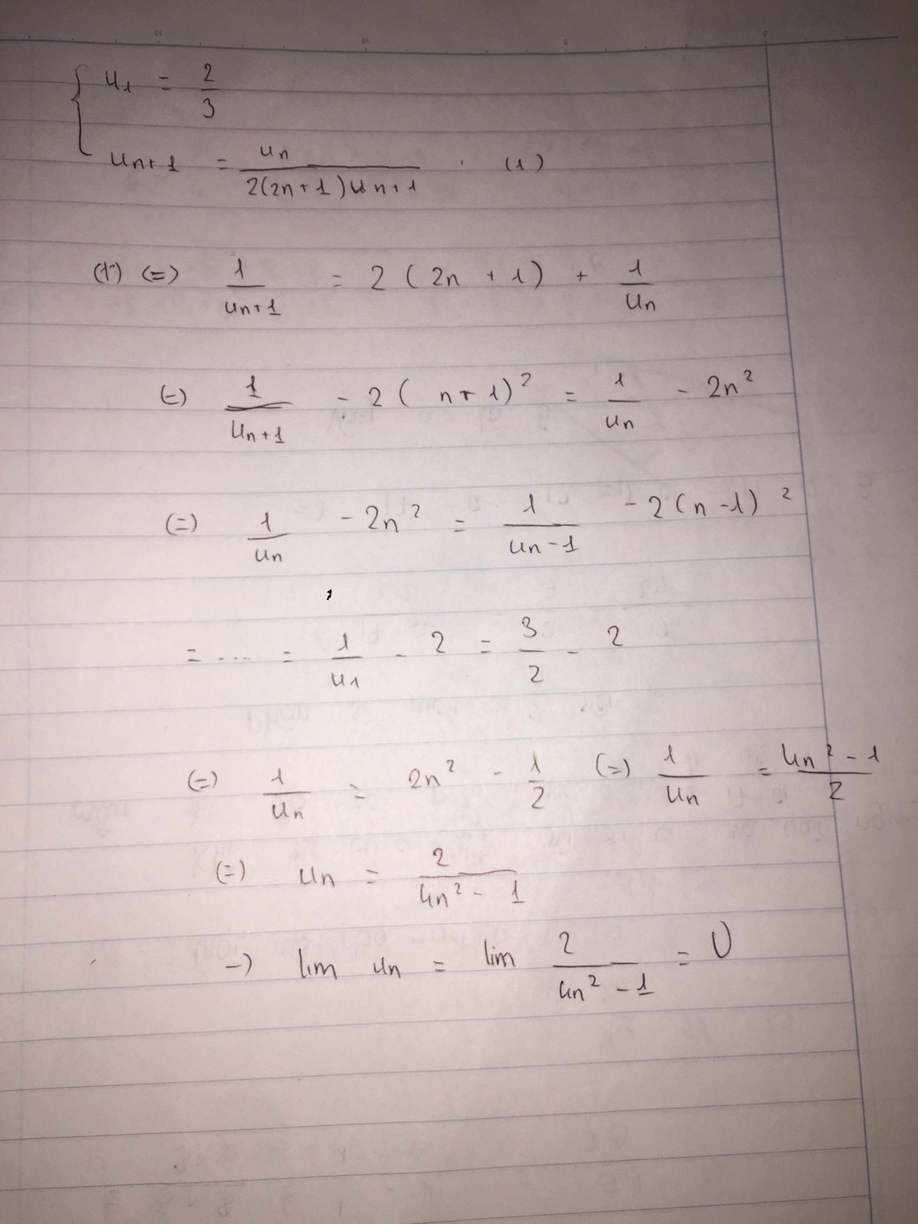\(u_n=\dfrac{1}{2^2-1}+\dfrac{1}{3^2-1}+...+\dfrac{1}{n^2-1}\)

\(=\dfrac{1}{\left(2-1\right)\left(2+1\right)}+\dfrac{1}{\left(3-1\right)\left(3+1\right)}+...+\dfrac{1}{\left(n-1\right)\left(n+1\right)}\)

\(=\dfrac{1}{1\cdot3}+\dfrac{1}{2\cdot4}+...+\dfrac{1}{\left(n-1\right)\cdot\left(n+1\right)}\)

\(=\dfrac{1}{2}\left(\dfrac{2}{1\cdot3}+\dfrac{2}{2\cdot4}+...+\dfrac{2}{\left(n-1\right)\left(n+1\right)}\right)\)

\(=\dfrac{1}{2}\cdot\left(1-\dfrac{1}{3}+\dfrac{1}{2}-\dfrac{1}{4}+...+\dfrac{1}{\left(n-1\right)}-\dfrac{1}{\left(n+1\right)}\right)\)

\(=\dfrac{1}{2}\left(1+\dfrac{1}{2}-\dfrac{1}{n+1}\right)=\dfrac{1}{2}\cdot\left(\dfrac{3}{2}-\dfrac{1}{n+1}\right)\)

\(=\dfrac{3}{4}-\dfrac{1}{2n+2}\)

\(\lim\limits u_n=\lim\limits\left(\dfrac{3}{4}-\dfrac{1}{2n+2}\right)\)

\(=\lim\limits\dfrac{3}{4}-\lim\limits\dfrac{1}{2n+2}\)

\(=\dfrac{3}{4}-\lim\limits\dfrac{\dfrac{1}{n}}{2+\dfrac{1}{n}}\)

=3/4

=>Chọn A

Bạn tham khảo câu trả lời của anh Lâm

https://hoc24.vn/cau-hoi/.334447965337

a) Để chứng minh rằng Un > 1 đối với mọi N và Un là dãy tăng, ta có thể sử dụng phương pháp quy nạp.

Bước cơ sở: Ta thấy rằng u1 = 2 > 1.

Bước giả sử: Giả sử đúng đối với một số nguyên k ≥ 1, tức là uk > 1.

Bước bước: Ta sẽ chứng minh rằng uk+1 > 1. Từ công thức cho dãy (Un), ta có:

uk+1 = uk-2015 + uk + 1/uk - uk + 3

Vì uk > 1 (theo giả thiết giả sử), ta có uk - 2015 > 0 và uk + 3 > 0. Do đó, uk+1 > 0.

Vì vậy, ta có uk+1 > 1, và đẳng thức này đúng đối với mọi số nguyên k ≥ 1.

Do đó, ta chứng minh được rằng Un > 1 đối với mọi N và Un là dãy tăng.

b) Để tính limn∑i=11uk - i + 2, ta có thể sử dụng định nghĩa của dãy (Un) và công thức tổng của dãy số aritmeti.

Từ công thức cho dãy (Un), ta có:

uk - i + 2 = uk - 2015 - i + uk + 1 - i + uk + 2 - i

Vì Un là dãy tăng, ta có thể viết lại công thức trên như sau:

uk - i + 2 = uk - 2015 - i + uk + 1 - i + uk + 2 - i

= (uk+1 - 2015 + uk + 1) - (uk - 2015 + uk) + (uk+1 - uk)

= 2uk+1 - 2uk + 2015

Do đó, ta có thể viết lại tổng như sau:

∑i=11uk - i + 2 = 2∑i=11uk+1 - 2∑i=11uk + 2015∑i=1

= 2(u12 - u2) + 2015(12)

Với giá trị cụ thể của u12 và u2, ta có thể tính được tổng trên.

a.

\(u_n=\dfrac{1}{\left(2-1\right)\left(2+1\right)}+\dfrac{1}{\left(3-1\right)\left(3+1\right)}+...+\dfrac{1}{\left(n-1\right)\left(n+1\right)}\)

\(=\dfrac{1}{1.3}+\dfrac{1}{2.4}+\dfrac{1}{3.5}+...+\dfrac{1}{\left(n-2\right)n}+\dfrac{1}{\left(n-1\right)\left(n+1\right)}\)

\(=\dfrac{1}{2}\left(1-\dfrac{1}{3}+\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{n-2}-\dfrac{1}{n}+\dfrac{1}{n-1}-\dfrac{1}{n+1}\right)\)

\(=\dfrac{1}{2}\left(1+\dfrac{1}{2}-\dfrac{1}{n}-\dfrac{1}{n+1}\right)\)

\(=\dfrac{1}{2}\left(\dfrac{3}{2}-\dfrac{1}{n}-\dfrac{1}{n+1}\right)\)

\(\Rightarrow\lim u_n=\lim\left(\dfrac{1}{2}\left(\dfrac{3}{2}-\dfrac{1}{n}-\dfrac{1}{n+1}\right)\right)=\dfrac{1}{2}.\dfrac{3}{2}=\dfrac{3}{4}\)

b.

\(u_n=\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{n\left(n+1\right)}\)

\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{n}-\dfrac{1}{n+1}\)

\(=1-\dfrac{1}{n+1}\)

\(\Rightarrow\lim u_n=\lim\left(1-\dfrac{1}{n+1}\right)=1\)

c.

\(1+2+...+n=\dfrac{n\left(n+1\right)}{2}\)

\(\Rightarrow\dfrac{1}{1+2+...+n}=\dfrac{2}{n\left(n+1\right)}=\dfrac{2}{n}-\dfrac{2}{n+1}\)

\(\Rightarrow u_n=1+\dfrac{2}{2}-\dfrac{2}{3}+\dfrac{2}{3}-\dfrac{2}{4}+...+\dfrac{2}{n}-\dfrac{2}{n+1}\)

\(=1+1-\dfrac{2}{n+1}=2-\dfrac{2}{n+1}\)

\(\Rightarrow\lim u_n=\lim\left(2-\dfrac{2}{n+1}\right)=2\)