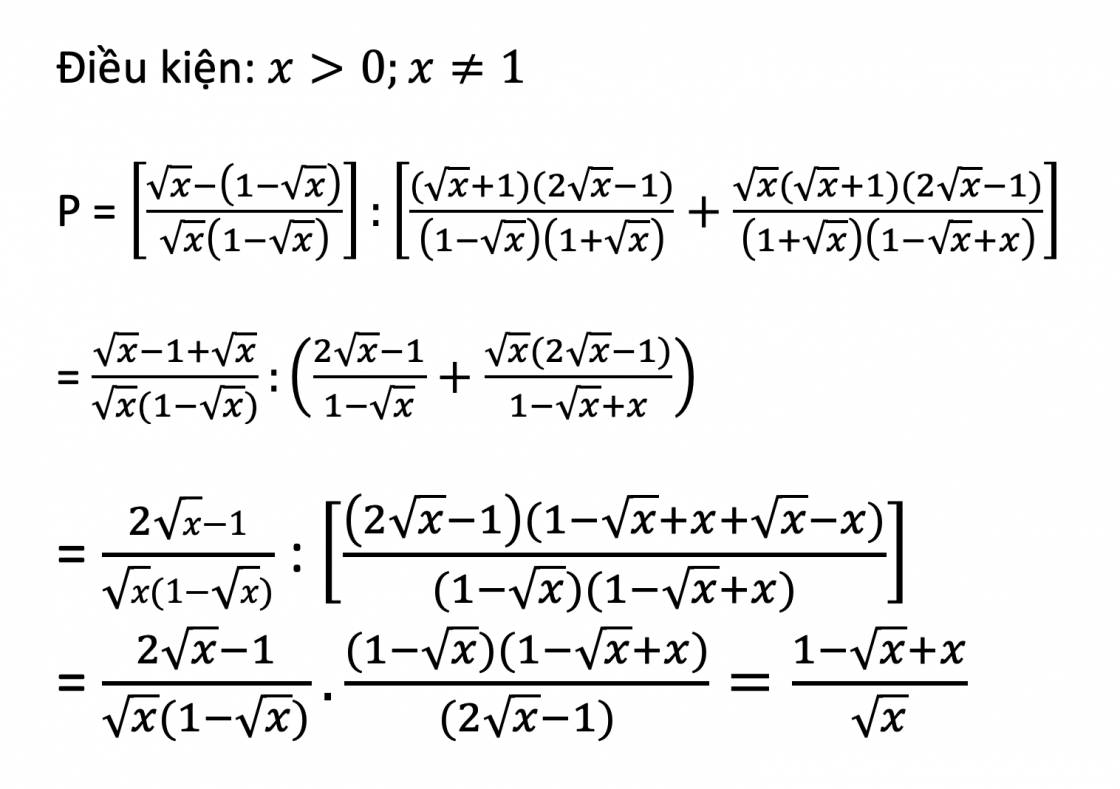\(3\sqrt{x}+\dfrac{3}{\sqrt{x}}< 2x+\dfrac{1}{2x}-7\)

Những câu hỏi liên quan
giải pt :
a, (x+5)(2-x)=3\(\sqrt{x^2+3x}\)
b, \(\sqrt[3]{\dfrac{2x}{x+1}}+\sqrt[3]{\dfrac{1}{2}+\dfrac{1}{2x}}=2\)
c,\(\sqrt[5]{\dfrac{16x}{x-1}}+\sqrt[5]{\dfrac{x-1}{16x}}=\dfrac{5}{2}\)
d, \(\sqrt{5x^2+10x+1}=7-2x-x^2\)
e, \(\sqrt{2x^2+4x+1}=1-2x-x^2\)
tính giới hạn của các hàm số sau:a, limx→0dfrac{sqrt{1+x}-sqrt{1-x}}{sqrt[3]{1+x}-sqrt{1-x}}b, limx→0(dfrac{1}{x}-dfrac{1}{x^2})c, limx→+∞ dfrac{x^4-x^3+11}{2x-7}d, limx→5 ( dfrac{7}{left(x-1right)^2}.dfrac{2x+1}{2x-3} )
Đọc tiếp
tính giới hạn của các hàm số sau:
a, limx→0\(\dfrac{\sqrt{1+x}-\sqrt{1-x}}{\sqrt[3]{1+x}-\sqrt{1-x}}\)
b, limx→0(\(\dfrac{1}{x}-\dfrac{1}{x^2}\))
c, limx→+∞ \(\dfrac{x^4-x^3+11}{2x-7}\)
d, limx→5 ( \(\dfrac{7}{\left(x-1\right)^2}.\dfrac{2x+1}{2x-3}\) )
a. Áp dụng công thức L'Hospital:
\(\lim\limits_{x\to 0}\frac{\sqrt{x+1}-\sqrt{1-x}}{\sqrt[3]{x+1}-\sqrt{1-x}}=\lim\limits_{x\to 0}\frac{\frac{1}{2}(x+1)^{\frac{-1}{2}}+\frac{1}{2}(1-x)^{\frac{-1}{2}}}{\frac{1}{3}(x+1)^{\frac{-2}{3}}+\frac{1}{2}(1-x)^{\frac{-1}{2}}}=\frac{1}{\frac{5}{6}}=\frac{6}{5}\)
b.
\(\lim\limits_{x\to 0}(\frac{1}{x}-\frac{1}{x^2})=\lim\limits_{x\to 0}\frac{x-1}{x^2}=-\infty\)
Đúng 1
Bình luận (0)
c. Áp dụng quy tắc L'Hospital:
\(\lim\limits_{x\to +\infty}\frac{x^4-x^3+11}{2x-7}=\lim\limits_{x\to +\infty}\frac{4x^3-3x^2}{2}=+\infty \)
d.
\(\lim\limits_{x\to 5}\frac{7}{(x-1)^2}.\frac{2x+1}{2x-3}=\frac{7}{(5-1)^2}.\frac{2.5+11}{2.5-3}=\frac{11}{16}\)
Đúng 1
Bình luận (0)
Giải phương trình:
1. sqrt{2x^2+4x+7}x^4+4x^3+3x^2-2x-7
2. dfrac{4}{x}+sqrt{x-dfrac{1}{x}}x+sqrt{2x-dfrac{5}{x}}
3. dfrac{6-2x}{sqrt{5-x}}+dfrac{6+2x}{sqrt{5+x}}dfrac{8}{3}
4. x^2+1-left(x+1right)sqrt{x^2-2x+3}0
5. 2sqrt{2x+4}+4sqrt{2-x}sqrt{9x^2+16}
6. left(2x+7right)sqrt{2x+7}x^2+9x+7
Đọc tiếp
Giải phương trình:
1. \(\sqrt{2x^2+4x+7}=x^4+4x^3+3x^2-2x-7\)
2. \(\dfrac{4}{x}+\sqrt{x-\dfrac{1}{x}}=x+\sqrt{2x-\dfrac{5}{x}}\)
3. \(\dfrac{6-2x}{\sqrt{5-x}}+\dfrac{6+2x}{\sqrt{5+x}}=\dfrac{8}{3}\)
4. \(x^2+1-\left(x+1\right)\sqrt{x^2-2x+3}=0\)
5. \(2\sqrt{2x+4}+4\sqrt{2-x}=\sqrt{9x^2+16}\)
6. \(\left(2x+7\right)\sqrt{2x+7}=x^2+9x+7\)
a) lim \(\dfrac{x\sqrt{x^2+1}-2x+1}{^3\sqrt{2x^3-2}+1}\)
x-> -∞
b) lim \(\dfrac{\left(2x+1\right)^3\left(x+2\right)^4}{\left(3-2x\right)^7}\)
x-> -∞
c) lim \(\dfrac{\sqrt{4x^2+x}+^3\sqrt{8x^3+x-1}}{^4\sqrt{x^4+3}}\)
x-> +∞
a/ \(=\lim\limits_{x\rightarrow-\infty}\dfrac{\dfrac{x\sqrt{x^2+1}}{x}-\dfrac{2x}{x}+\dfrac{1}{x}}{\sqrt[3]{\dfrac{2x^3}{x^3}-\dfrac{2x}{x^3}}+\dfrac{1}{x}}=0\)
b/ \(=\lim\limits_{x\rightarrow-\infty}\dfrac{\dfrac{8x^7}{x^7}}{\dfrac{\left(-2x^7\right)}{x^7}}=-\dfrac{8}{2^7}\)
c/ \(=\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt{\dfrac{4x^2}{x^2}+\dfrac{x}{x^2}}+\sqrt[3]{\dfrac{8x^3}{x^3}+\dfrac{x}{x^3}-\dfrac{1}{x^3}}}{\sqrt[4]{\dfrac{x^4}{x^4}+\dfrac{3}{x^4}}}=\dfrac{2+2}{1}=4\)
Đúng 1
Bình luận (0)
tìm điều kiện bài toán:
a) \(y=\dfrac{1}{x}-\dfrac{\sqrt{2x-1}}{x^2-3x+2}\)
b) \(y=\dfrac{1}{x^2-1}-\sqrt{7-2x}\)
c) \(y=\dfrac{2}{x}+\dfrac{3}{4-2x+x^2}\)
d) \(y=\sqrt{25-x^2}-2\sqrt{x}+3\)
Lời giải:
a.
\(\left\{\begin{matrix} x\neq 0\\ 2x-1\geq 0\\ x^2-3x+2=(x-1)(x-2)\neq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\neq 0\\ x\geq \frac{1}{2}\\ x\neq 1; x\neq 2\end{matrix}\right.\)
$\Leftrightarrow x\geq \frac{1}{2}; x\neq 1; x\neq 2$
b. \(\left\{\begin{matrix}
x^2-1=(x-1)(x+1)\neq 0\\
7-2x\geq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
x\neq \pm 1\\
x\leq \frac{7}{2}\end{matrix}\right.\)
c.
\(\left\{\begin{matrix} x\neq 0\\ 4-2x+x^2\neq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\neq 0\\ (x-1)^2+3\neq 0\end{matrix}\right.\Leftrightarrow x\neq 0\)
d.
\(\left\{\begin{matrix} 25-x^2=(5-x)(5+x)\geq 0\\ x\geq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} -5\leq x\leq 5\\ x\geq 0\end{matrix}\right.\Leftrightarrow 0\leq x\leq 5\)
Đúng 1
Bình luận (0)
a) \(y=\dfrac{1}{x}-\dfrac{\sqrt[]{2x-1}}{x^2-3x+2}\)
Điều kiện \(\) \(2x-1\ge0;x\ne0;x^2-3x+2\ne0\)
\(\Leftrightarrow x\ge\dfrac{1}{2};x\ne0;\left(x-1\right)\left(x-2\right)\ne0\)
\(\Leftrightarrow x\ge\dfrac{1}{2};x\ne0;x\ne1;x\ne2\)
Đúng 0
Bình luận (0)
a) \(x\ge\dfrac{1}{2};x\ne1;x\ne2\)
b) \(x\le\dfrac{7}{2};x\ne\pm1\)
c) \(x\ne0\)
d) \(0\le x\le5\)
Đúng 0
Bình luận (0)
Giải các phương trình sau:1) sqrt{3x^2+5x+8}-sqrt{3x^2+5x+1}12) x^2-2x-12+4sqrt{left(4-xright)left(2+xright)}03) 3sqrt{x}+dfrac{3}{2sqrt{x}}2x+dfrac{1}{2x}-74) sqrt{x}-dfrac{4}{sqrt{x+2}}+sqrt{x+2}05)left(x-7right)sqrt{dfrac{x+3}{x-7}}x+46) 2sqrt{x-4}+sqrt{x-1}sqrt{2x-3}+sqrt{4x-16}7) sqrt{x+2sqrt{x-1}}+sqrt{x-2sqrt{x-1}}dfrac{x+3}{2}Giúp mình với ajk, mink đang cần gấp
Đọc tiếp
Giải các phương trình sau:
1) \(\sqrt{3x^2+5x+8}-\sqrt{3x^2+5x+1}=1\)
2) \(x^2-2x-12+4\sqrt{\left(4-x\right)\left(2+x\right)}=0\)
3) \(3\sqrt{x}+\dfrac{3}{2\sqrt{x}}=2x+\dfrac{1}{2x}-7\)
4) \(\sqrt{x}-\dfrac{4}{\sqrt{x+2}}+\sqrt{x+2}=0\)
5)\(\left(x-7\right)\sqrt{\dfrac{x+3}{x-7}}=x+4\)
6) \(2\sqrt{x-4}+\sqrt{x-1}=\sqrt{2x-3}+\sqrt{4x-16}\)
7) \(\sqrt{x+2\sqrt{x-1}}+\sqrt{x-2\sqrt{x-1}}=\dfrac{x+3}{2}\)
Giúp mình với ajk, mink đang cần gấp
Giải phương trình:
1. \(5x^2+2x+10=7\sqrt{x^4+4}\)
2. \(\dfrac{4}{x}+\sqrt{x-\dfrac{1}{x}}=x+\sqrt{2x-\dfrac{5}{x}}\)
3. \(\sqrt{x^2+2x}=\sqrt{3x^2+4x+1}-\sqrt{3x^2+4x+1}\)
Tìm x
1) \(\sqrt{\dfrac{3x-1}{x+2}}=2\)
2)\(\sqrt{\dfrac{5x-7}{2x- 1}}=2\)
3)\(\dfrac{\sqrt{x}-2}{\sqrt{x}+1}=\dfrac{\sqrt{x}-1}{\sqrt{x}+3}\)
4) \(\dfrac{\sqrt{x}-3}{\sqrt{x}+2}=\dfrac{\sqrt{x}-2}{\sqrt{x}+1}\)
1: \(\Leftrightarrow\dfrac{3x-1}{x+2}=4\)
=>4x+8=3x-1
=>x=-9
2: \(\Leftrightarrow\dfrac{5x-7}{2x-1}=4\)
=>8x-4=5x-7
=>3x=-3
=>x=-1
3: ĐKXD: x>=0
\(PT\Leftrightarrow\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)=\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)\)
=>\(x+\sqrt{x}-6=x-1\)
=>căn x=-1+6=5
=>x=25
4: ĐKXĐ: x>=0
PT =>\(\left(\sqrt{x}-3\right)\left(\sqrt{x}+1\right)=\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)\)
=>x-2*căn x-3=x-4
=>-2căn x-3=-4
=>2căn x+3=4
=>2căn x=1
=>căn x=1/2
=>x=1/4
Đúng 0
Bình luận (0)
P=\(\left(\dfrac{1}{1-\sqrt{x}}-\dfrac{1}{\sqrt{x}}\right)\):\(\left(\dfrac{2x+\sqrt{x}-1}{1-x}+\dfrac{2x\sqrt{x}+x-\sqrt{x}}{1+x\sqrt{x}}\right)\)
Rút gọnP
Tính giá trị của P với \(x=7-4\sqrt{3}\)