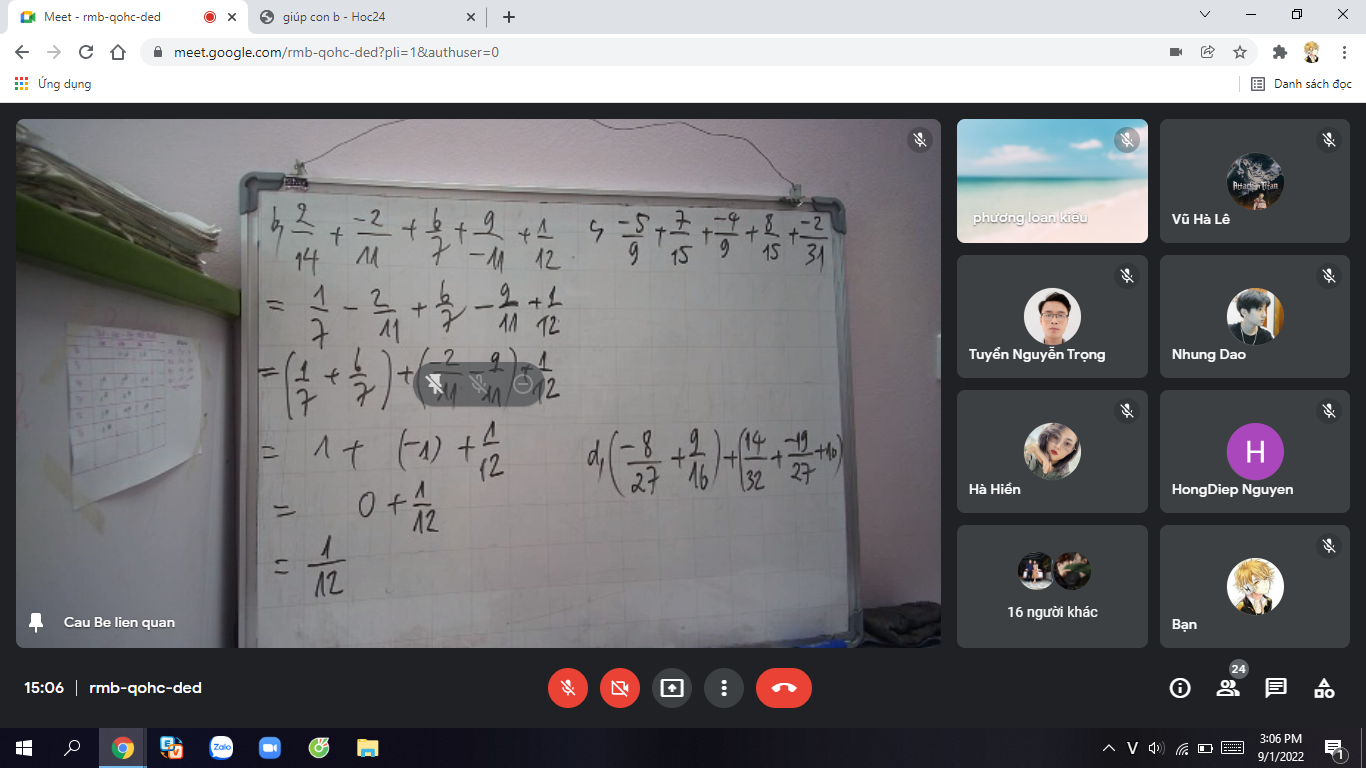
giúp câu d với
gấpppppppppppppppppppppppppppp
GIÚP EM CÂU C,D BÀI 1,CÂU B,D BÀI 2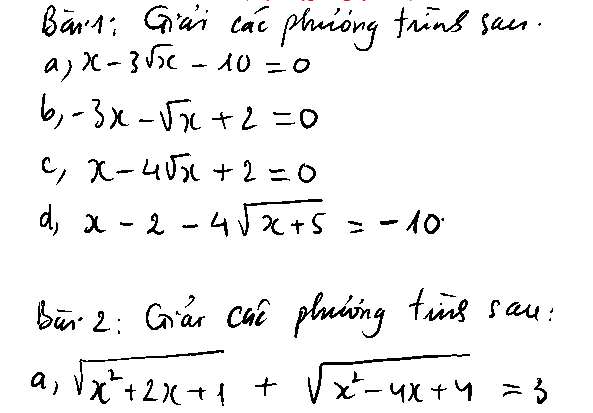
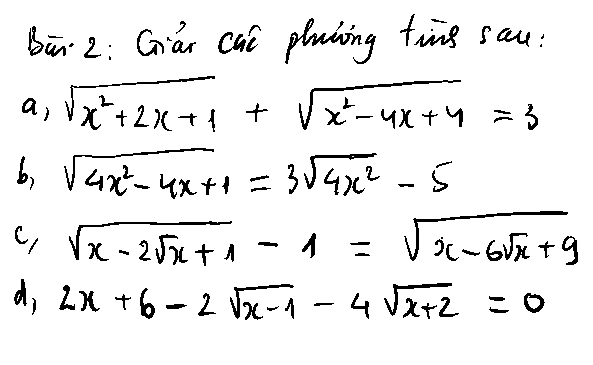
1.
d, ĐK: \(x\ge-5\)
\(x-2-4\sqrt{x+5}=-10\)
\(\Leftrightarrow x+5-4\sqrt{x+5}+3=0\)
\(\Leftrightarrow\left(\sqrt{x+5}-1\right)\left(\sqrt{x+5}-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x+5}=1\\\sqrt{x+5}=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x+5=1\\x+5=9\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-4\\x=4\end{matrix}\right.\)
\(\Leftrightarrow x=\pm4\left(tm\right)\)
2.
ĐK: \(x\in R\)
\(\sqrt{x^2+2x+1}+\sqrt{x^2-4x+4}=3\)
\(\Leftrightarrow\sqrt{\left(x+1\right)^2}+\sqrt{\left(x-2\right)^2}=3\)
\(\Leftrightarrow\left|x+1\right|+\left|x-2\right|=3\)
Áp dụng BĐT \(\left|a\right|+\left|b\right|\ge\left|a+b\right|\).
\(\left|x+1\right|+\left|x-2\right|=\left|x+1\right|+\left|2-x\right|\ge\left|x+1+2-x\right|=3\)
Đẳng thức xảy ra khi:
\(\left(x+1\right)\left(2-x\right)\ge0\)
\(\Leftrightarrow-1\le x\le2\)
a)\(\left(\left(\sqrt{x}\right)^2-2\sqrt{x}\dfrac{3}{2}+\dfrac{9}{4}\right)-\dfrac{49}{4}=0\)
⇒\(\left(\sqrt{x}-\dfrac{3}{2}\right)^2=\dfrac{49}{4}\)
TH1:\(\sqrt{x}-\dfrac{3}{2}=\dfrac{7}{2}\)⇒\(\sqrt{x}=5\)⇒x=25
TH2:\(\sqrt{x}-\dfrac{3}{2}=\dfrac{-7}{2}\)⇒\(\sqrt{x}=-2\) vì \(\sqrt{x}\)≥0 loại
Giúp em câu c với câu d
a. \(\Delta'=1^2-1.\left(-3\right)=4>0\)
Do \(\Delta'>0\) nên PT luôn có 2 nghiệm phân biệt.
b. Dựa vào hệ thức Vi - ét, ta có:
\(\left\{{}\begin{matrix}S=x_1+x_2=-\dfrac{b}{a}=-\dfrac{2}{1}=-2\\P=x_1x_2=\dfrac{c}{a}=-\dfrac{3}{1}=-3\end{matrix}\right.\)
c. \(U=\left(x_2-x_2\right)^2-2x_1^2x_2^2\)
\(=x_1^2-2x_1x_2+x_2^2-2\left(x_1x_2\right)^2\)
\(=x_1^2+x^2_2-2x_1x_2-2\left(x_1x_2\right)^2\)
\(=\left(x_1+x_2\right)^2-2x_1x_2-2\left(x_1x_2\right)^2\)
\(=\left(-2\right)^2-2.\left(-3\right)-2.\left(-3\right)^2\)
\(=-8\)
d. \(A=\dfrac{1}{x_1}+\dfrac{1}{x_2}-3\)
\(=\dfrac{x_2}{x_1x_2}+\dfrac{x_1}{x_1x_2}-3\)
\(=\dfrac{x_1+x_2}{x_1x_2}-3\)
\(=\dfrac{-2}{-3}-3\)
\(=-\dfrac{7}{3}\)
giúp mình bài 6 với ạ trừ câu a còn các câu b,c,d, giúp mình với ạ
\(b,N=\left(2x-1\right)^2-4\ge-4\\ N_{min}=-4\Leftrightarrow x=\dfrac{1}{2}\\ c,P=\left(2x-5\right)^2+6\left(2x-5\right)+9-4\\ P=\left(2x-5+3\right)^2-4=\left(2x-2\right)^2-4\ge-4\\ P_{min}=-4\Leftrightarrow x=1\\ d,Q=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+1\\ Q=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1\\ Q_{min}=1\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
6a.
$M=x^2-x+1=(x^2-x+\frac{1}{4})+\frac{3}{4}$
$=(x-\frac{1}{2})^2+\frac{3}{4}\geq \frac{3}{4}$
Vậy $M_{\min}=\frac{3}{4}$ khi $x-\frac{1}{2}=0\Leftrightarrow x=\frac{1}{2}$
Giúp em câu b với câu d với ạ.
Giúp mình câu d và câu e với ạ

d: Xét ΔABC có
BK,CH là đường cao
BK cắt CH tại I
=>I là trực tâm
=>AI vuông góc BC
mà HF vuông góc BC
nên AI//HF
e: Xét ΔABC cân tại A có góc BAC=60 độ
nên ΔABC đều
Xét ΔABC đều có I là trực tâm
nên I là tâm đường tròn ngoại tiếp ΔABC
=>IA=IB=IC
giúp em bài 1 câu c câu d với ạ!!!

`D=(sqrt{3}.sqrt{5-2sqrt6})/(sqrt3-sqrt2)-1/(2-sqrt3)`
`=(sqrt3*sqrt{3-2sqrt{3}.sqrt2+2})/(sqrt3-sqrt2)-(2+sqrt3)/(4-3)`
`=(sqrt3.sqrt{(sqrt3-sqrt2)^2})/(sqrt3-sqrt2)-2-sqrt3`
`=sqrt3-2-sqrt3=-2`
c) Ta có: \(C=\sqrt{\dfrac{3\sqrt{5}+1}{2\sqrt{5}-3}}\cdot\left(\sqrt{10}-\sqrt{2}\right)\)
\(=\dfrac{\sqrt{\left(3\sqrt{5}+1\right)\left(2\sqrt{5}-3\right)}}{2\sqrt{5}-3}\cdot\left(\sqrt{10}-\sqrt{2}\right)\)
\(=\dfrac{\sqrt{30-9\sqrt{5}+2\sqrt{5}-3}}{2\sqrt{5}-3}\cdot\left(\sqrt{10}-\sqrt{2}\right)\)
\(=\dfrac{\sqrt{27-7\sqrt{5}}}{2\sqrt{5}-3}\cdot\left(\sqrt{10}-\sqrt{2}\right)\)
\(=\dfrac{\sqrt{54-14\sqrt{5}}}{2\sqrt{10}-3\sqrt{2}}\cdot\left(\sqrt{10}-\sqrt{2}\right)\)
\(=\dfrac{\left(7-\sqrt{5}\right)\cdot\sqrt{2}\left(\sqrt{5}-1\right)}{\sqrt{2}\cdot\left(2\sqrt{5}-3\right)}\)
\(=\dfrac{7\sqrt{5}-7-5+\sqrt{5}}{2\sqrt{5}-3}\)
\(=\dfrac{8\sqrt{5}-12}{2\sqrt{5}-3}\)
\(=\dfrac{4\left(2\sqrt{5}-3\right)}{2\sqrt{5}-3}=4\)
Giúp mình câu d với câu e.Mình đang cần gấp!!
a: Thay x=0 và y=3 vào (d), ta được:
2m-5=3
hay m=4
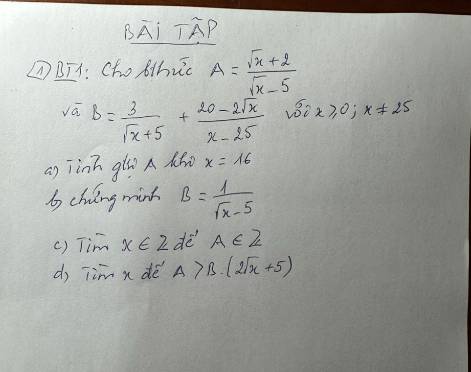
giải giúp mình câu C với câu D với ạ
a) \(A=\dfrac{\sqrt[]{x}+2}{\sqrt[]{x}-5}\) có nghĩa \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\sqrt[]{x}-5\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\sqrt[]{x}\ne5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x\ne25\end{matrix}\right.\)
Khi \(x=16\Rightarrow A=\dfrac{\sqrt[]{16}+2}{\sqrt[]{16}-5}=\dfrac{4+2}{4-5}=-6\)
b) \(B=\dfrac{3}{\sqrt[]{x}+5}+\dfrac{20-2\sqrt[]{x}}{x-25}\)
B có nghĩa \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x-25\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x\ne25\end{matrix}\right.\)
\(\Leftrightarrow B=\dfrac{3\left(\sqrt[]{x}-5\right)+20-2\sqrt[]{x}}{\left(\sqrt[]{x}+5\right)\left(\sqrt[]{x}-5\right)}\)
\(\Leftrightarrow B=\dfrac{3\sqrt[]{x}-15+20-2\sqrt[]{x}}{\left(\sqrt[]{x}+5\right)\left(\sqrt[]{x}-5\right)}\)
\(\Leftrightarrow B=\dfrac{\sqrt[]{x}+5}{\left(\sqrt[]{x}+5\right)\left(\sqrt[]{x}-5\right)}\)
\(\Leftrightarrow B=\dfrac{1}{\sqrt[]{x}-5}\left(dpcm\right)\)
c) \(A=\dfrac{\sqrt[]{x}+2}{\sqrt[]{x}-5}\in Z\left(x\in Z\right)\)
\(\Leftrightarrow\sqrt[]{x}+2⋮\sqrt[]{x}-5\)
\(\Leftrightarrow\sqrt[]{x}+2-\left(\sqrt[]{x}-5\right)⋮\sqrt[]{x}-5\)
\(\Leftrightarrow\sqrt[]{x}+2-\sqrt[]{x}+5⋮\sqrt[]{x}-5\)
\(\Leftrightarrow7⋮\sqrt[]{x}-5\)
\(\Leftrightarrow\sqrt[]{x}-5\in U\left(7\right)=\left\{-1;1;-7;7\right\}\)
\(\Leftrightarrow x\in\left\{16;36;144\right\}\)
d) \(A>B\left(2\sqrt[]{x}+5\right)\)
\(\Leftrightarrow\dfrac{\sqrt[]{x}+2}{\sqrt[]{x}-5}>\dfrac{1}{\sqrt[]{x}-5}\left(2\sqrt[]{x}+5\right)\)
\(\Leftrightarrow\sqrt[]{x}+2>2\sqrt[]{x}+5\)
\(\Leftrightarrow\sqrt[]{x}< -3\)
mà \(\sqrt[]{x}\ge0\)
\(\Leftrightarrow x\in\varnothing\)