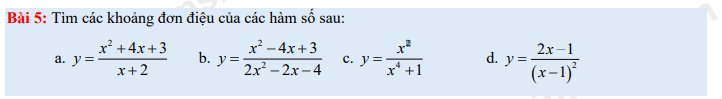b: ĐKXĐ: \(2x^2-2x-4<>0\)
=>\(x^2-x-2<>0\)
=>(x-2)(x+1)<>0
=>x∉{2;-1}
Ta có: \(y=\frac{x^2-4x+3}{2x^2-2x-4}\)
=>\(y^{\prime}=\frac{\left(x^2-4x+3\right)^{\prime}\left(2x^2-2x-4\right)-\left(x^2-4x+3\right)\left(2x^2-2x-4\right)^{\prime}}{\left(2x^2-2x-4\right)^2}\)
=>\(y^{\prime}=\frac{\left(2x-4\right)\left(2x^2-2x-4\right)-\left(x^2-4x+3\right)\left(4x-2\right)}{\left(2x^2-2x-4\right)^2}\)
=>\(y^{\prime}=\frac{4x^3-4x^2-8x-8x^2+8x+16-\left(4x^3-2x^2-16x^2+8x+12x-6\right)}{\left(2x^2-2x-4\right)^2}\)
=>\(y^{\prime}=\frac{4x^3-12x^2+16-\left(4x^3-18x^2+20x-6\right)}{\left(2x^2-2x-4\right)^2}=\frac{6x^2-20x+22}{\left(2x^2-2x-4\right)^2}\)
Đặt y'>0
=>\(6x^2-20x+22>0\)
=>\(3x^2-10x+11>0\)
=>\(x^2-\frac{10}{3}x+\frac{11}{3}>0\)
=>\(x^2-\frac{10}{3}x+\frac{25}{9}+\frac{11}{3}-\frac{25}{9}>0\)
=>\(\left(x-\frac53\right)^2+\frac89>0\) (luôn đúng)
=>Hàm số đồng biến trên các khoảng xác định của nó
=>Hàm số đồng biến trên các khoảng (-∞;-1); (-1;2); (2;+∞)
d: \(y=\frac{2x-1}{\left(x-1\right)^2}\) (ĐKXĐ: x<>1)
=>\(y=\frac{2x-1}{x^2-2x+1}\)
=>\(y^{\prime}=\frac{\left(2x-1\right)^{\prime}\left(x^2-2x+1\right)-\left(2x-1\right)\left(x^2-2x+1\right)^{\prime}}{\left(x^2-2x+1\right)^2}\)
=>\(y^{\prime}=\frac{2\left(x^2-2x+1\right)-\left(2x-1\right)\left(2x-2\right)}{\left(x^2-2x+1\right)^2}=\frac{2x^2-4x+2-\left(4x^2-6x+2\right)}{\left(x^2-2x+1\right)^2}\)
\(=\frac{2x^2-4x+2-4x^2+6x-2}{\left(x^2-2x+1\right)^2}=\frac{-2x^2+2x}{\left(x^2-2x+1\right)^2}=\frac{-2x\left(x-1\right)}{\left(x^2-2x+1\right)^2}\)
Đặt y'<0
=>-2x(x-1)<0
=>x(x-1)>0
=>\(\left[\begin{array}{l}x>1\\ x<0\end{array}\right.\)
=>Hàm số nghịch biến trên các khoảng (1;+∞) và (-∞;0)
Đặt y'>0
=>-2x(x-1)>0
=>x(x-1)<0
=>0<x<1
=>Hàm số đồng biến trên khoảng (0;1)