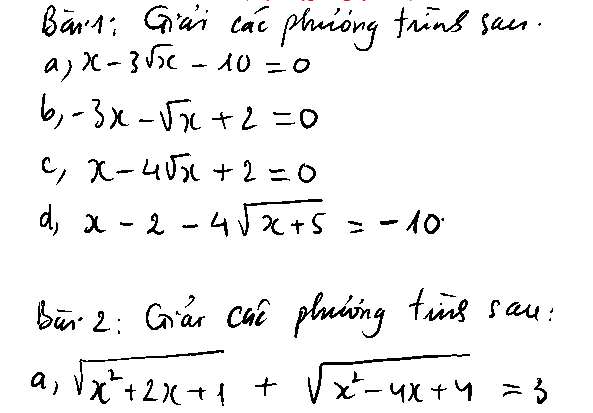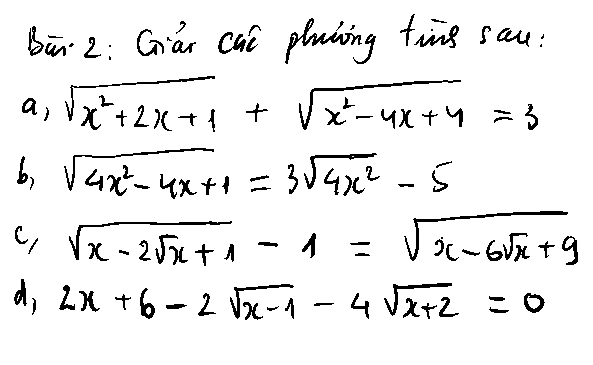a. \(\Delta'=1^2-1.\left(-3\right)=4>0\)
Do \(\Delta'>0\) nên PT luôn có 2 nghiệm phân biệt.
b. Dựa vào hệ thức Vi - ét, ta có:
\(\left\{{}\begin{matrix}S=x_1+x_2=-\dfrac{b}{a}=-\dfrac{2}{1}=-2\\P=x_1x_2=\dfrac{c}{a}=-\dfrac{3}{1}=-3\end{matrix}\right.\)
c. \(U=\left(x_2-x_2\right)^2-2x_1^2x_2^2\)
\(=x_1^2-2x_1x_2+x_2^2-2\left(x_1x_2\right)^2\)
\(=x_1^2+x^2_2-2x_1x_2-2\left(x_1x_2\right)^2\)
\(=\left(x_1+x_2\right)^2-2x_1x_2-2\left(x_1x_2\right)^2\)
\(=\left(-2\right)^2-2.\left(-3\right)-2.\left(-3\right)^2\)
\(=-8\)
d. \(A=\dfrac{1}{x_1}+\dfrac{1}{x_2}-3\)
\(=\dfrac{x_2}{x_1x_2}+\dfrac{x_1}{x_1x_2}-3\)
\(=\dfrac{x_1+x_2}{x_1x_2}-3\)
\(=\dfrac{-2}{-3}-3\)
\(=-\dfrac{7}{3}\)
Em cần giúp câu c và d ạ, mn giúp em với em đang cần gấp
