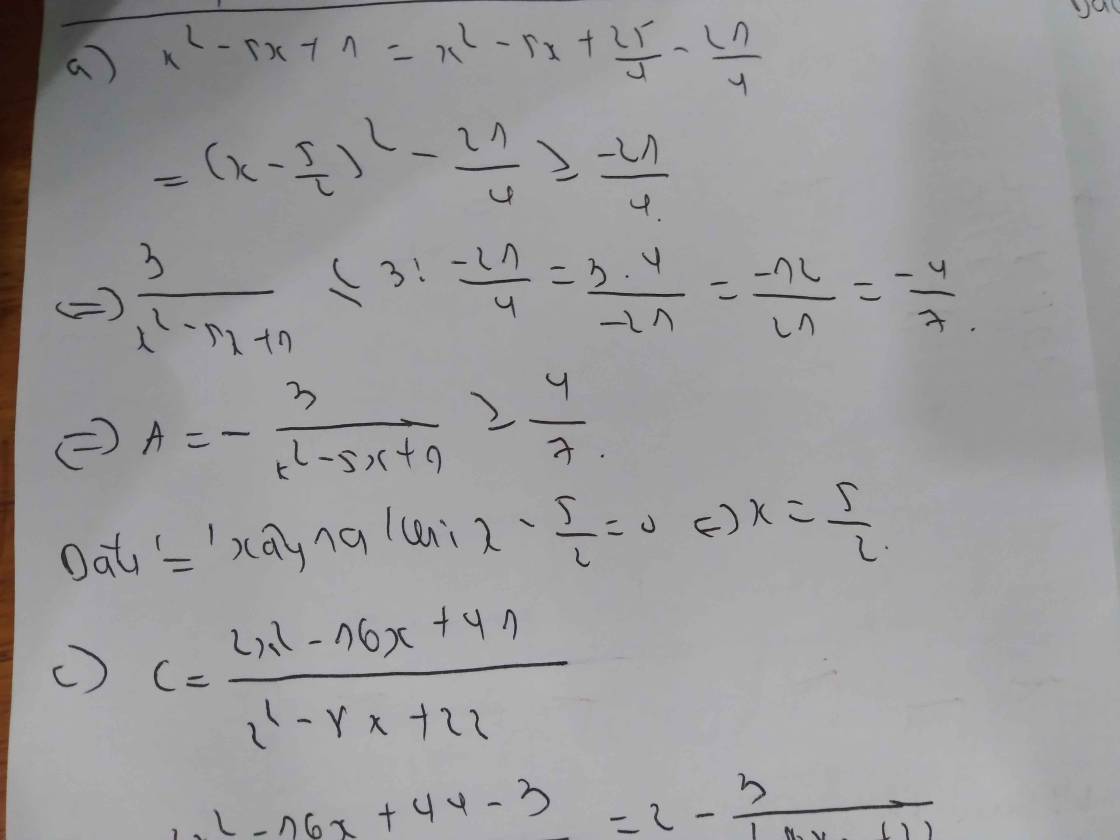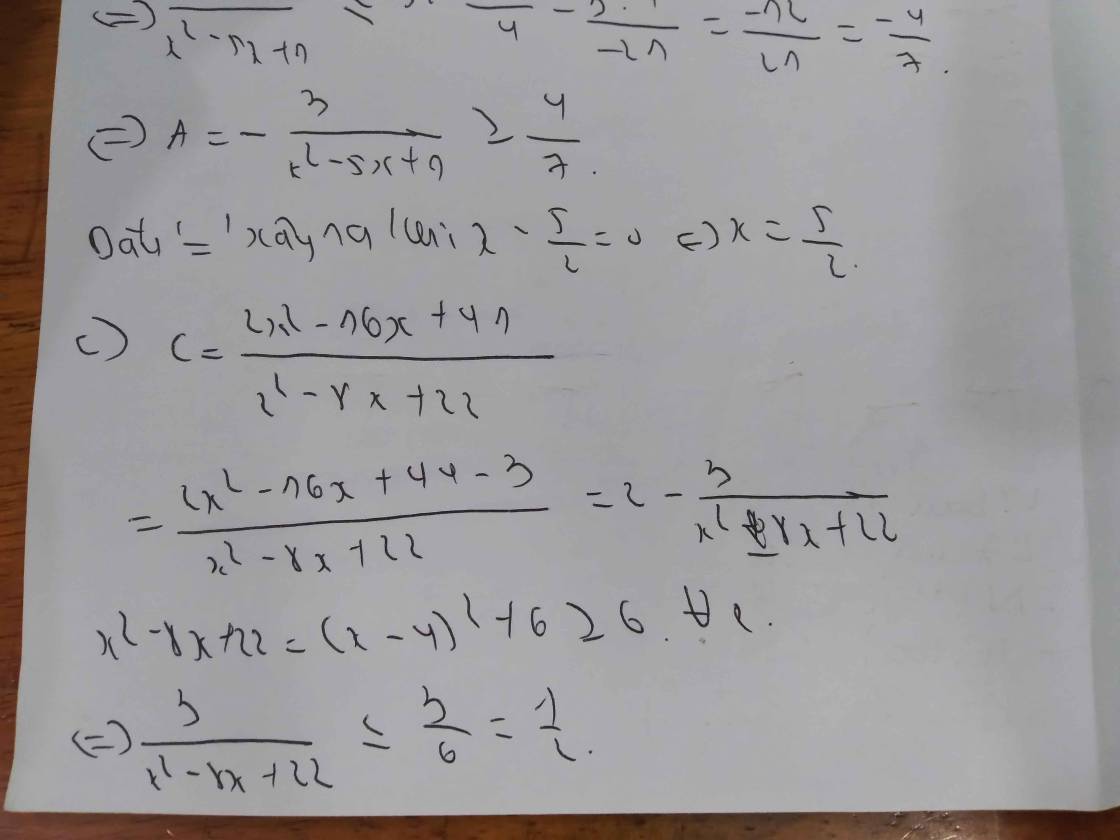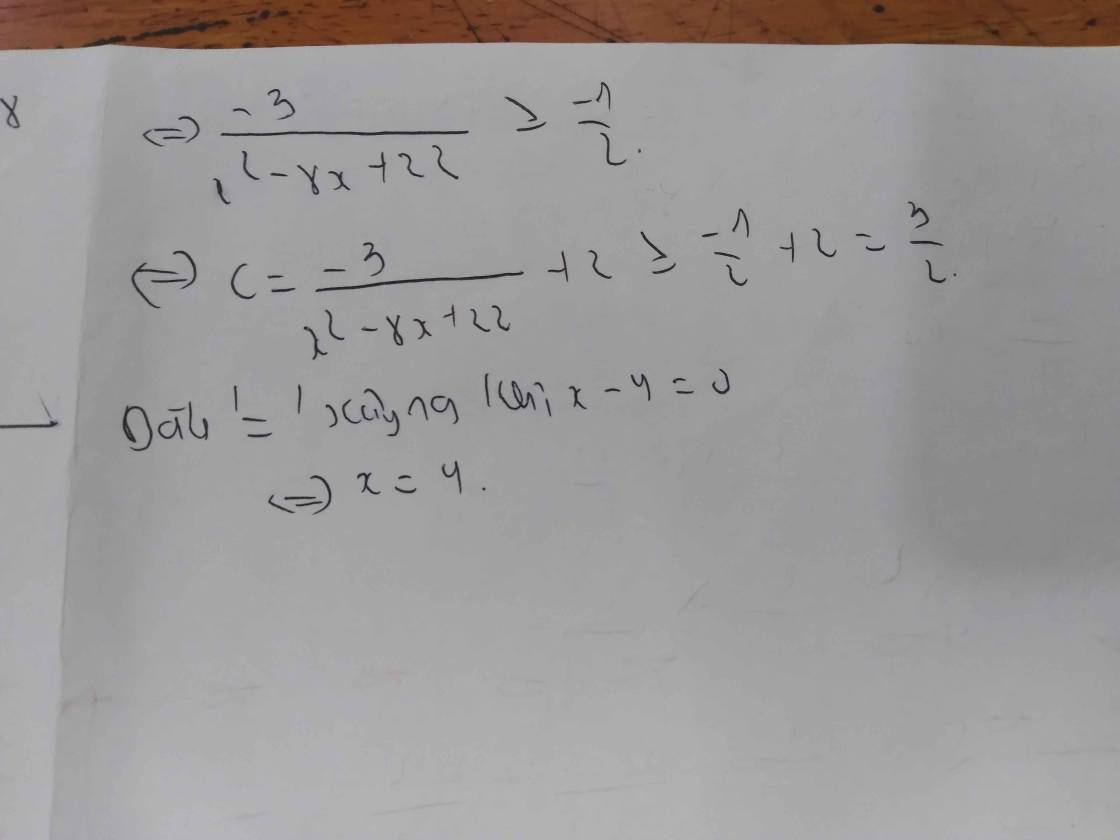Tìm giá trị lớn nhất của C= \(\dfrac{x^2-4x-4}{x^2-4x+5}\)

Những câu hỏi liên quan
Tìm giá trị lớn nhất hoặc giá trị nhỏ nhất của các biểu thức sau:
a) S= \(\dfrac{3}{2x^2+2x+3}\)
b) T= \(\dfrac{5}{3x^2+4x+15}\)
c) V= \(\dfrac{1}{-x^2+2x-2}\)
d) X= \(\dfrac{2}{-4x^2+8x-5}\)
a) Tìm giá trị nhỏ nhất của biểu thức: S= \(\dfrac{5x^4+4x^2+10}{x^4+2}\)
b) Tìm giá trị lớn nhất của biểu thức: T=\(\dfrac{2x^4-4x^2+8}{x^4+4}\)
c) Cho a là hằng số và a>0. Tìm giá trị nhỏ nhất của biểu thức: M=\(\dfrac{8y^8+2a\left(y-3\right)^2+2a^2}{4y^8+a^2}\)
Tìm giá trị lớn nhất (GTNN) của các biểu thức sau:
A= \(\dfrac{4+5\left|1-2x\right|}{7}\)
B= \(\dfrac{x^2+4x-6}{3}\)
C= \(\dfrac{5}{x^2-2x+3}\)
. a.Tìm giá trị nhỏ nhất của biểu thức:
A = x^2 -2x +9
B = x^2+ 6x - 3
C = (x -1 )(x - 3) + 9
b. Tìm giá trị lớn nhất của biểu thức:
E = -x^2 – 4x +7
F = 5 - 4x^2 + 4
\(A=\left(x-1\right)^2+8\ge8\\ A_{min}=8\Leftrightarrow x=1\\ B=\left(x+3\right)^2-12\ge-12\\ B_{min}=-12\Leftrightarrow x=-3\\ C=x^2-4x+3+9=\left(x-2\right)^2+8\ge8\\ C_{min}=8\Leftrightarrow x=2\\ E=-\left(x+2\right)^2+11\le11\\ E_{max}=11\Leftrightarrow x=-2\\ F=9-4x^2\le9\\ F_{max}=9\Leftrightarrow x=0\)
Đúng 2
Bình luận (0)
tìm giá trị nhỏ nhất của biểu thức\(A=x^2-4x+\dfrac{1}{x^2-4x+4}+5\)
`A=x^2-4x+1/(x^2-4x+4)+5`
`=x^2-4x+4+1/(x^2-4x+4)+1`
Áp dụng BĐT cosi với 2 số dương ta có:
`x^2-4x+4+1/(x^2-4x+4)=(x-2)^2+1/(x-2)^2>=2`
`=>x^2-4x+4+1/(x^2-4x+4)+1>=3`
Dấu "=" xảy ra khi `(x-2)^2=1/(x-2)^2`
`<=>(x-2)^4=1`
`<=>` $\left[ \begin{array}{l}x=3\\x=1\end{array} \right.$
Vậy `min_A=3<=>` $\left[ \begin{array}{l}x=3\\x=1\end{array} \right.$
Đúng 2
Bình luận (0)
Tìm giá trị nhỏ nhất hoặc lớn nhất của các biểu thức sau
a) A= \(\dfrac{-3}{x^2-5x+1}\)
b) B=\(\dfrac{2x^2+4x+4}{x^2}\)
c) C= \(\dfrac{2x^2-16x+41}{x^2-8x+22}\)
Với x là số thực,tìm giá trị nhỏ nhất của các biểu thức sau:
1, A = 2x^2 + 4x + 1
2, B = 3x - x^2 + 4
3, C = 8x - 4x^2
4, D = \(\dfrac{1}{4x^2-4x+5}\)
HELPPPPP Me T.T
\(A=2x^2+4x+1=2\left(x^2+2x+1\right)-1=2\left(x+1\right)^2-1\ge-1\)
\(A_{min}=-1\) khi \(x=-1\)
Câu B chỉ có max, ko có min
\(B=-x^2+3x+4=-\left(x^2-3x+\dfrac{9}{4}\right)+\dfrac{25}{4}=-\left(x-\dfrac{3}{2}\right)^2+\dfrac{25}{4}\le\dfrac{25}{4}\)
\(B_{max}=\dfrac{25}{4}\) khi \(x=\dfrac{3}{2}\)
Câu C cũng chỉ có max, không có min
\(C=-4x^2+8x=-4\left(x^2-2x+1\right)+4=-4\left(x-1\right)^2+4\le4\)
\(C_{max}=4\) khi \(x=1\)
Câu D cũng chỉ có max, không có min
\(D=\dfrac{3}{4x^2-4x+1+4}=\dfrac{3}{\left(2x-1\right)^2+4}\le\dfrac{3}{4}\)
\(C_{max}=\dfrac{3}{4}\) khi \(x=\dfrac{1}{2}\)
(4 câu có 3 câu sai đề)
Đúng 1
Bình luận (5)
Tìm giá trị nhỏ nhất của các biểu thức sauAx^2-4x+1 B4x^2+4x+11 Cleft(x-1right)left(x+3right)left(x+2right)left(x+6right)D2x^2+y^2-2xy+2x-4y+9 Tìm giá trị lớn nhất của các biểu thức sauE5-8x-x^2F4x-x^2+1
Đọc tiếp
Tìm giá trị nhỏ nhất của các biểu thức sau
A=\(x^2-4x+1\) \(B=4x^2+4x+11\)
\(C=\left(x-1\right)\left(x+3\right)\left(x+2\right)\left(x+6\right)\)
\(D=2x^2+y^2-2xy+2x-4y+9\)
Tìm giá trị lớn nhất của các biểu thức sau
\(E=5-8x-x^2\)
\(F=4x-x^2+1\)
Tìm giá trị lớn nhất và giá trị nhỏ nhất của P = \(\dfrac{3x^2-4x+8}{x^2+2}\)
\(P=\dfrac{2\left(x^2+2\right)+x^2-4x+4}{x^2+2}=2+\dfrac{\left(x-2\right)^2}{x^2+2}\ge2\)
\(P=\dfrac{5\left(x^2+2\right)-2x^2-4x-2}{x^2+2}=5-\dfrac{2\left(x+1\right)^2}{x^2+2}\le5\)
Đúng 0
Bình luận (0)