Biết tích ∫ 1 4 f t d t = 3 và ∫ 1 2 f t d t = 3 . Phát biểu nào sau đây nhận giá trị đúng?
A. ∫ 2 4 f t d t = 3
B. ∫ 2 4 f x d x = - 3
C. ∫ 2 4 f x d x = 3
D. ∫ 2 4 f x d x = 0
Những câu hỏi liên quan
Cho hàm số f(x) xác định trên R{±1} thỏa mãn f (x)
1
x
2
-
1
. Biết f(–3) +f(3) 0 và f
-
1
2
+ f
1
2
2. Giá trị T f(–2) + f(0) + f(4) bằng: A. ...
Đọc tiếp
Cho hàm số f(x) xác định trên R\{±1} thỏa mãn f '(x) = 1 x 2 - 1 . Biết f(–3) +f(3) = 0 và f - 1 2 + f 1 2 = 2. Giá trị T = f(–2) + f(0) + f(4) bằng:
A. T = 1 2 ln 9 5
B. T = 2 + 1 2 ln 9 5
C. T = 3 + 1 2 ln 9 5
D. T = 1 + 1 2 ln 9 5
Đáp án D.
Phương pháp: 
Cách giải: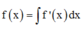 
=> f(x) =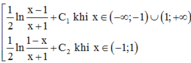 
=> f(x) =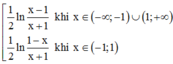 
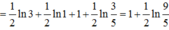
Đúng 0
Bình luận (0)
tìm các hệ số a,b,c,d của đa thức f(x)=ax^3+bx^2+cx+d biết f(0)=-5;f(1)=4;f(2)=31;f(3)=88
Đúng 0
Bình luận (2)
cho hàm số : y= f(x) = ax+4
a, tìm a, biết x= -2 thì y= -4
b, với a vừa tìm được ở câu a , hãy tính
f(-1/2) ; f (-3) ; f (5)
f(4/3) ; f(0,5) ; f(1/1/2)
a: Thay x=-2 và y=-4 vào y=ax+4, ta được:
-2a+4=-4
=>-2a=-8
=>a=4
=>y=4x+4
b: f(-1/2)=4*(-1/2)+4=4-2=2
f(-3)=-12+4=-8
f(5)=4*5+4=24
f(4/3)=4*4/3+4=16/3+4=32/3
f(1/2)=4*1/2+4=2+4=6
f(3/2)=4*3/2+4=6+4=10
Đúng 0
Bình luận (0)
Cho hàm số f (x) = 9^x / (9^x + 3) .Biết a + b= 3, tính S = f (a) + f (b - 2). A. S=1. B. S=2. C. S=1/4. D. S=3/4
Lời giải:
\(a+b=3\Rightarrow a+(b-2)=1\Rightarrow b-2=1-a\)
Ta có:
\(f(x)=\frac{9^x}{9^x+3}\Rightarrow f(a)=\frac{9^a}{9^a+3}\) (1)
\(f(b-2)=f(1-a)=\frac{9^{1-a}}{9^{1-a}+3}=\frac{9}{9^a\left(\frac{9}{9^a}+3\right)}\)
\(=\frac{9}{9+3.9^a}=\frac{3}{3+9^a}\) (2)
Từ (1),(2) suy ra \(f(a)+f(b-2)=\frac{9^a}{9^a+3}+\frac{3}{3+9^a}=\frac{9^a+3}{9^a+3}=1\)
Đáp án A
Đúng 0
Bình luận (0)
cho y f(x) x-1/x-2 a) Tính f(1), f(-1), f(0), f(2)...
Đọc tiếp
cho y = f(x) = x-1/x-2 a) Tính f(1), f(-1), f(0), f(2) b) Cho f(x) = 2. Tìm x c) Tìm x thuộc Z để y thuộc Z d) Tìm a biết f(a) = 5
a: \(f\left(1\right)=\dfrac{1-1}{1-2}=-1\)
\(f\left(-1\right)=\dfrac{-1-1}{-1-2}=-\dfrac{2}{-3}=\dfrac{2}{3}\)
\(f\left(0\right)=\dfrac{0-1}{0-2}=\dfrac{1}{2}\)
\(f\left(2\right)=\dfrac{2-1}{2-2}=\varnothing\)
b: f(x)=2 nên x-1=2x-4
=>2x-4=x-1
=>x=3
c: Để y là số ngyên thì \(x-2+1⋮x-2\)
\(\Leftrightarrow x-2\in\left\{1;-1\right\}\)
hay \(x\in\left\{3;1\right\}\)
Đúng 0
Bình luận (0)
cho y f(x) x-1/ x-2 a) Tính f(1), f(-1), f(0), f(2)...
Đọc tiếp
cho y = f(x) = x-1/ x-2 a) Tính f(1), f(-1), f(0), f(2) b) Cho f(x) = 2.Tìm x c) Tìm x thuộc Z để y thuộc Z d) Tìm a biết f(a) = 5
\(y=f\left(x\right)=\dfrac{x-1}{x-2}\)
a)
\(y=f\left(1\right)=\dfrac{1-1}{1-2}=\dfrac{0}{-1}=0\)
\(y=f\left(-1\right)=\dfrac{\left(-1\right)-1}{\left(-1\right)-2}=\dfrac{-1-1}{-1-2}=\dfrac{-\left(1+1\right)}{-\left(1+2\right)}=\dfrac{-2}{-3}=\dfrac{2}{3}\)
\(y=f\left(0\right)=\dfrac{0-1}{0-2}=\dfrac{-1}{-2}=\dfrac{1}{2}\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tìm đa thức bậc 4 biết : f(0) = -1; f(1) = 2; f(2) = 31; f(3) =47
Bài 1 : Tính giá trị biết với x = -1 ; y=3 :
A=x^2y-y+xy^2-x
B=x^2y^2+xy+x^3+y^3
C=2x+xy^2-x^2y-2y
D=3x^3-2y^3+6x^2y^2+xy
Bài 2 : f(x)= 3x-6 ; g(t)=-4t+8 . Tìm giá trị biến để :
a ) f(x)=0;g(t)=0
b) f(x)=1;g(t)=1
c) f(x)>0;g(t)>0
d ) f(x)<0;g(t)<1
Bài 1:
\(A=x^2y-y+xy^2-x=\left(x^2y+xy^2\right)-\left(x+y\right)\\ =xy\left(x+y\right)-\left(x+y\right)=\left(x+y\right)\left(xy-1\right)\)
Voqis x=-1;y=3 ta có:
\(A=\left(-1+3\right)\left(-1\cdot3-1\right)=2\cdot\left(-4\right)=-8\)
b) \(B=x^2y^2+xy+x^3+y^3=\left(x^2y^2+x^3\right)+\left(xy+y^3\right)\\ =x^2\left(y^2+x\right)+y\left(x+y^2\right)=\left(x+y^2\right)\left(x^2+y\right)\)
Với x=-1;y=3 ta có:
\(B=\left(-1+3^2\right)\left(-1^2+3\right)=8\cdot2=16\)
c) \(C=2x+xy^2-x^2y-2y=\left(2x-2y\right)+\left(xy^2-x^2y\right)\\ =2\left(x-y\right)+xy\left(y-x\right)=\left(x-y\right)\left(2-xy\right)\)
Với x=-1;y=3 ta có:
\(C=\left(-1-3\right)\left(2-\left(-1\right)\cdot3\right)=-4\cdot5=-20\)
d) phân tích tt
Đúng 0
Bình luận (0)
Cho đa thức bậc 3 f(x) biết:
f(0)=10; f(1)=12; f(2)=4;f(3)=1 Tính f(10)= ?
Lời giải :
Đa thức bậc 3 có dạng :\(ax^3+bx^2+cx+d=0\)
Theo giả thiết bài ra ta có hệ phương trình :
\(\left\{{}\begin{matrix}f\left(0\right)=d=10\\f\left(1\right)=a+b+c+10=12\\f\left(2\right)=8a+4b+2c+10=4\\f\left(3\right)=27a+9b+3c+10=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}d=10\\a+b+c=2\\8a+4b+2c=-6\\27a+9b+3c=-9\end{matrix}\right.\)
Giai trên máy ta tìm được a , b , c , d lần lượt là :
\(\left\{{}\begin{matrix}a=2,5\\b=-12,5\\c=12\\d=10\end{matrix}\right.\)
Đa thức f(x) có dạng : \(2,5x^3-12,5x^2+12x+10\)
Nhập biểu thức đó bấm CALC , 10 . Ta tìm được số dư là 1380
Đúng 0
Bình luận (0)
Cho hàm số y = f(x) = ax
a) Biết a = 2 tính f(1); f(-2); f(-4)
b) Tìm a biết: f(2) = 4; Vẽ đồ thị hàm số khi a = 2; a = -3
c) Trong các điểm sau điếm nào thuộc đồ thị hàm số khi a = 2
A(1;4) B(-1;-2) C(-2;4) D(-2;4)
a, Có a = 2 \(\Rightarrow\)f(1) = 2 . 1 = 2
f(-2) = 2 . (-2)=-4
f(-4) = 2 . (-4) = -8
b, Theo công thức y = f(x) = a.x
mà f(x) =4 \(\Rightarrow\)a = 4 : 2 =2
CÂU C KHÓ QUÁ , 2 CÂU TRÊN MÌNH CHẮC ĐÚNG KHOẢNG 70 % \(\rightarrow\)80%
CHÚC BẠN HC TỐT