Cho điểm A x 0 ; y 0 và đường thẳng ∆: ax + by + c = 0. Khoảng các từ A đến đường thẳng ∆ được cho bởi công thức
A. a x 0 + b y 0 + c a 2 + b 2
B. a x 0 + b y 0 + c a 2 + b 2
C. a x 0 + b y 0 + c a 2 + b 2
D. a x 0 + b y 0 + c a 2 + b 2
Cho đường thẳng Δ : x – y + 2 = 0 và hai điểm O(0; 0), A(2; 0).
a, Tìm điểm đối xứng của O qua Δ.
b, Tìm điểm M trên Δ sao cho độ dài đường gấp khúc OMA ngắn nhất.
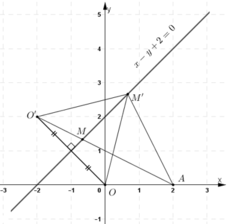
a, Cách 1: Gọi O’ là điểm đối xứng với O qua (Δ)
⇒ OO’ ⊥ Δ tại trung điểm I của OO’.
+ (Δ) nhận 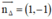 là một vtpt ⇒ (Δ) nhận
là một vtpt ⇒ (Δ) nhận 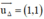 là một vtcp
là một vtcp
OO’ ⊥ Δ ⇒ OO’ nhận 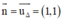 là một vtpt. Mà O(0, 0) ∈ OO’
là một vtpt. Mà O(0, 0) ∈ OO’
⇒ Phương trình đường thẳng OO’: x + y = 0.
+ I là giao OO’ và Δ nên tọa độ của I là nghiệm của hệ phương trình:
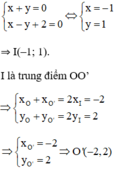
Cách 2: Gọi O’(x, y) là điểm đối xứng với O qua Δ.
+ Trung điểm I của OO’ là 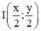
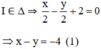
+ (Δ) nhận 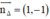 là một vtpt ⇒ (Δ) nhận
là một vtpt ⇒ (Δ) nhận 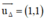 là một vtcp.
là một vtcp.
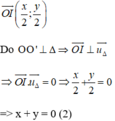
Từ (1) và (2) ta có hệ phương trình
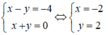
Vậy O’(–2; 2).
b)
+ Vì O và A nằm cùng một nửa mặt phẳng bờ là đường thẳng Δ nên đoạn thẳng OA không cắt Δ.
O’ và A thuộc hai nửa mặt phẳng khác nhau bờ là đường thẳng Δ nên O’A cắt Δ.
Do O’ đối xứng với O qua đường thẳng ∆ nên ∆ là đường trung trực của đoạn thẳng OO’, với mọi M ∈ Δ ta có MO = MO’.
Độ dài đường gấp khúc OMA bằng OM + MA = O’M + MA ≥ O’A.
⇒ O’M + MA ngắn nhất khi O’M + MA = O’A ⇔ M là giao điểm của O’A và Δ.
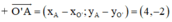
⇒ O’A nhận 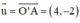 là một vtcp
là một vtcp
⇒ O’A nhận 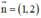 là một vtpt. Mà A(2; 0) ∈ O’A
là một vtpt. Mà A(2; 0) ∈ O’A
⇒ Phương trình đường thẳng O’A : 1(x - 2) + 2(y - 0)= 0 hay x + 2y – 2 = 0.
M là giao điểm của O’A và Δ nên tọa độ điểm M là nghiệm của hệ :
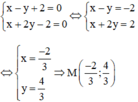
Vậy điểm M cần tìm là 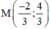
Cho đường thẳng Δ : x – y + 2 = 0 và hai điểm O(0; 0), A(2; 0). Tìm điểm M trên Δ sao cho độ dài đường gấp khúc OMA ngắn nhất.
Trước hết ta thấy O, A nằm trên cùng một mặt phẳng bờ \(\Delta\).
Qua A kẻ đường thẳng d vuông góc với \(\Delta\) tại H.
Đường thẳng d có phương trình: \(x+y-2=0\)
\(\Rightarrow H\) có tọa độ là nghiệm hệ \(\left\{{}\begin{matrix}x-y+2=0\\x+y-2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=2\end{matrix}\right.\Rightarrow H=\left(0;2\right)\)
Gọi A' là điểm đối xứng với A qua d
\(\Rightarrow\left\{{}\begin{matrix}x_{A'}=2x_H-x_A=-2\\y_{A'}=2y_H-y_A=4\end{matrix}\right.\Rightarrow A'=\left(-2;4\right)\)
\(\Rightarrow OA'=2\sqrt{5}\)
Phương trình đường thẳng OA': \(2x+y=0\)
Khi đó: \(OM+MA=OM+MA'\ge OA'=2\sqrt{5}\)
\(min=2\sqrt{5}\Leftrightarrow M\) là giao điểm của \(\Delta\) và OA'
\(\Leftrightarrow M\) có tọa độ là nghiệm hệ \(\left\{{}\begin{matrix}x-y+2=0\\2x+y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{2}{3}\\y=\dfrac{4}{3}\end{matrix}\right.\Rightarrow M=\left(-\dfrac{2}{3};\dfrac{4}{3}\right)\)
Lời giải:
Vì $M$ thuộc $\Delta$ nên $M$ có tọa độ $(a-2,a)$
Độ dài đường gấp khúc $OMA$ là:
$OM+MA=\sqrt{a^2+(a-2)^2}+\sqrt{(a-4)^2+a^2}$
$=\sqrt{2}.(\sqrt{(a-1)^2+1}+\sqrt{(2-a)^2+2^2})$
$\geq \sqrt{2}.\sqrt{(a-1+2-a)^2+(1+2)^2}$ (theo BĐT Mincopxky)
$=2\sqrt{5}$
Vậy $OMA$ min bằng $2\sqrt{5}$. Giá trị này đạt tại $a=\frac{4}{3}$
Vậy $M(\frac{-2}{3},\frac{4}{3})$
26. Cho đg thẳng denta 7x +10y -15=0 . Trong các điểm M (1;-3) , N(0;4) , P(8;0) , Q(1;5) điểm nào cách xa đg thẳng denta nhất?
A. M
B. N
C. P
D. Q
25. Khoảnh cách giữa 2 đg thẳng denta 1: 7x +y -3=0 và denta 2: 7x +y +12=0
A. 15
B. 9
C. 9/√50
D. 3√2/2
23. Cho 3 điểm A(0;1) , B(12;5) , C(-3;5) . Đg thẳng nào sau đây cách đều 3 điểm A,B,C
A. -x +y +10=0
B. x -3y +4=0
C. 5x -y +1=0
D. x +y =0
22. Cho 2 điểm A(2;3) , B(1;4) . Đg thẳng nào sau đây cách đều 2 điểm A,B?
A. x -y+100=0
B. x -2y=0
C. x +y -1=0
D. x +2y=0
Cho hàm số f ( x ) = 3 x + a - 1 k h i x ≤ 0 1 + 2 x - 1 x k h i x > 0 . Tìm tất cả giá trị của a để hàm số đã cho liên tục tại điểm x = 0
A. a = 1.
B. a = 3.
C. a = 2.
D. a = 4.
23. Cho 3 điểm A(0;1) , B(12;5), C(-3;5).Đg thẳng nào sau đây cách đều 3 điểm A, B, C
A -x +y +10=0
B x -3y +4=0
C 5x -y +1=0
D x +y=0
\(\overrightarrow{AB}=\left(12;4\right)=4\left(3;1\right)\) ; \(\overrightarrow{AC}=\left(-3;4\right)\); \(\overrightarrow{BC}=\left(-15;0\right)=-15\left(1;0\right)\)
\(\Rightarrow\) Đáp án B là đáp án chính xác (vì có vtpt vuông góc với 1 trong 3 cạnh của tam giác, 3 đáp án còn lại ko vuông góc nên đều loại)
Câu 14: (2,0 điểm) Phân tích đa thức sau thành nhân tử a) c) x2 + 25 – 10xd ) x3 – 8y3 Câu 15: (1,0 điểm) Tìm x, biết a) 3x.(x-1) + x-1=0 b) x2 - 6x = 0 Câu 16: (2,0 điểm) Cho tam giác vuông ABC vuông ở A có đường cao AH. Gọi E ,F lần lượt là hình chiếu của H lên AB và AC. a. So sánh AH và EF b. Tính độ dài HF biết AB = 6 cm, BC = 10 cm và BH = 3,6 cm. Câu 17: (1,0 điểm) Cho hình thang ABCD (AB// CD) có O là giao điểm 2 đường chéo. Qua O kẻ đường thẳng song song với AB cắt AD và BC lần lượt tại E và H. Chứng minh OE= OH.
Câu 17:
Xét ΔADC có OE//DC
nên \(\dfrac{OE}{DC}=\dfrac{AO}{AC}\left(1\right)\)
Xét ΔBDC có OH//DC
nên \(\dfrac{OH}{DC}=\dfrac{BO}{BD}\left(2\right)\)
Xét ΔOAB và ΔOCD có
\(\widehat{OAB}=\widehat{OCD}\)(hai góc so le trong, AB//CD)
\(\widehat{AOB}=\widehat{COD}\)(hai góc đối đỉnh)
Do đó: ΔOAB đồng dạng với ΔOCD
=>\(\dfrac{OA}{OC}=\dfrac{OB}{OD}\)
=>\(\dfrac{OC}{OA}=\dfrac{OD}{OB}\)
=>\(\dfrac{OC}{OA}+1=\dfrac{OD}{OB}+1\)
=>\(\dfrac{OC+OA}{OA}=\dfrac{OD+OB}{OB}\)
=>\(\dfrac{AC}{OA}=\dfrac{BD}{OB}\)
=>\(\dfrac{OA}{AC}=\dfrac{OB}{BD}\left(3\right)\)
Từ (1),(2),(3) suy ra \(\dfrac{OE}{DC}=\dfrac{OH}{DC}\)
=>OE=OH
Câu 15:
a: \(3x\left(x-1\right)+x-1=0\)
=>\(3x\left(x-1\right)+\left(x-1\right)=0\)
=>\(\left(x-1\right)\left(3x+1\right)=0\)
=>\(\left[{}\begin{matrix}x-1=0\\3x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{1}{3}\end{matrix}\right.\)
b: \(x^2-6x=0\)
=>\(x\cdot x-x\cdot6=0\)
=>x(x-6)=0
=>\(\left[{}\begin{matrix}x=0\\x-6=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=6\end{matrix}\right.\)
Cho hàm số f x = 3 x + a - 1 k h i x ≤ 0 1 + 2 x - 1 x k h i x > 0 . Tìm tất cả giá trị của a để hàm số đã cho liên tục tại điểm x = 0
A. a = 1
B. a = 3
C. a = 2
D. a = 4
Cho hàm số f x = 3 x + a - 1 k h i x ≤ 0 1 + 2 x - 1 x k h i x > 0 . Tìm tất cả giá trị của a để hàm số đã cho liên tục tại điểm x = 0.
A. a = 1
B. a = 3
C. a = 2
D. a = 4
cho tam giác ABC:
a, xác định I sao cho vectoIA +3vectoIB - 2vectoIC = 0
b, xác định điểm D sao cho 3vectoDB -2vectoDC = 0
c, cm 3 điểm A I D thằng hàng
a.
Gọi M là trung điểm AB, dựng hình bình hành BCMN \(\Rightarrow\overrightarrow{NM}=\overrightarrow{BC}\)
\(\overrightarrow{IA}+\overrightarrow{IB}+2\overrightarrow{IB}+2\overrightarrow{CI}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{IA}+\overrightarrow{IB}+2\overrightarrow{CB}=\overrightarrow{0}\Leftrightarrow2\overrightarrow{IM}+2\overrightarrow{CB}=0\)
\(\Leftrightarrow\overrightarrow{IM}=\overrightarrow{BC}\Leftrightarrow I\) trùng N
b.
\(\overrightarrow{DB}+2\overrightarrow{DB}+2\overrightarrow{CD}=\overrightarrow{0}\Leftrightarrow\overrightarrow{DB}+2\overrightarrow{CB}=0\)
\(\Leftrightarrow\overrightarrow{DB}=2\overrightarrow{BC}\Rightarrow D\) là điểm nằm trên tia đối của tia BC sao cho \(BD=2BC\)
c.
\(\overrightarrow{AI}=\overrightarrow{AM}+\overrightarrow{MI}=\frac{1}{2}\overrightarrow{AB}-\overrightarrow{BC}\)
\(\overrightarrow{AD}=\overrightarrow{AB}+\overrightarrow{BD}=\overrightarrow{AB}-2\overrightarrow{BC}=2\left(\frac{1}{2}\overrightarrow{AB}-\overrightarrow{BC}\right)=2\overrightarrow{AI}\)
\(\Rightarrow A;I;D\) thẳng hàng
Cho 3 điểm A(0;1) , B(12;5) , C(-3;0). Đ/t nào sau đây cách đều 3 điểm A,B,C ?
A. x-3y+4=0
B. -x+y+10=0
C. x+y=0
D. 5x-y+1=0
\(\overrightarrow{CA}=\left(3;1\right);\overrightarrow{CB}=\left(15;5\right)=5\left(3;1\right)=5\overrightarrow{CA}\)
\(\Rightarrow A;B;C\) thẳng hàng
\(\Rightarrow\) Đường thẳng cách đều 3 điểm A;B;C là đường thẳng song song với AC
\(\Rightarrow\) Là đường thẳng nhận \(\left(1;-3\right)\) là 1 vtpt
Đáp án A đúng