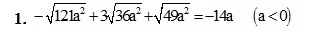\(\frac{\left(sin^2x\right)^2-\left(cos^2x\right)^2}{2sinxcosx}\)=\(\frac{\left(sin^2x+cos^2x\right).\left(sin^2x-cos^2x\right)}{2sinxcosx}\)=\(\frac{1.\left(sin^2x-cos^2x\right)}{2sinxcosx}\)=\(\frac{sin^2x-cos^2x}{sin2x}\)=\(\frac{\frac{1-cos2x}{2}-\frac{1+cos2x}{2}}{sin2x}\)=\(\frac{1-1-cos2x-cos2x}{2}.\frac{1}{sin2x}\)=\(\frac{-2cos2x}{2sin2x}=\frac{-cos2x}{sin2x}=-cot2x\left(đpcm\right)\)

Với \(n=0\Rightarrow0-0+0-0+0-0=0⋮24\left(đúng\right)\)

Với \(n=1\Rightarrow1-3+6-7+5-2=0⋮24\left(đúng\right)\)

G/s \(n=k\Rightarrow\left(k^6-3k^5+6k^4-7k^3+5k^2-2k\right)⋮24\)

\(\Rightarrow k\left(k^5-3k^4+6k^3-7k^2+5k-2\right)⋮24\\ \Rightarrow k\left(k+1\right)\left(k^2+k+1\right)\left(k^2-k+2\right)⋮24\)

Với \(n=k+1\), ta cần cm \(\left[\left(k+1\right)^6-3\left(k+1\right)^5+6\left(k+1\right)^4-7\left(k+1\right)^3+5\left(k+1\right)^2-2\left(k+1\right)\right]⋮24\)

Ta có \(\left(k+1\right)^6-3\left(k+1\right)^5+6\left(k+1\right)^4-7\left(k+1\right)^3+5\left(k+1\right)^2-2\left(k+1\right)\)

\(=\left(k+1\right)\left[\left(k+1\right)^5-3\left(k+1\right)^4+6\left(k+1\right)^3-7\left(k+1\right)+5\left(k+1\right)-2\right]\\ =\left(k+1\right)\left(k+1-1\right)\left[\left(k+1\right)^2-\left(k+1\right)+1\right]\left[\left(k+1\right)^2-\left(k+1\right)+2\right]\\ =k\left(k+1\right)\left(k^2+k+1\right)\left(k^2+k+2\right)\)

Mà theo GT quy nạp ta có \(k\left(k+1\right)\left(k^2+k+1\right)\left(k^2+k+2\right)⋮24\)

Vậy ta được đpcm

\(a,VT=\left(a^2-1\right)^2+4a^2\\ =a^4-2a^2+1+4a^2\\ =a^4+2a^2+1\\ =\left(a^2+1\right)^2 =VP\\ b,VT=\left(x-y\right)^2+\left(x+y\right)^2+2\left(x^2-y^2\right)\\ =x^2-2xy+y^2+x^2+y^2+2xy+2x^2-2y^2\\ =4x^2=VP\)

\(VT=\dfrac{x^2+xy+2xy+2y^2}{x^2\left(x+2y\right)-y^2\left(x+2y\right)}=\dfrac{\left(x+y\right)\left(x+2y\right)}{\left(x+2y\right)\left(x-y\right)\left(x+y\right)}=\dfrac{1}{x-y}\)

Bài 1a)

Áp dụng bất đẳng thức Cô-si cho từng cặp ta có

\(\left\{\begin{matrix}a+b\ge2\sqrt{ab}\\b+c\ge2\sqrt{bc}\\c+a\ge2\sqrt{ac}\end{matrix}\right.\)

\(=>\left(a+b\right)\left(b+c\right)\left(c+a\right)\ge2\sqrt{ab}.2\sqrt{bc}.2\sqrt{ac}\)

\(=>\left(a+b\right)\left(b+c\right)\left(a+c\right)\ge8\sqrt{\left(abc\right)^2}\)

\(=>\left(a+b\right)\left(b+c\right)\left(a+c\right)\ge8abc\) ( điều phải chứng minh )

Bài 1b)

Áp dụng bất đẳng thức Cô-si bộ 3 số cho từng cặp ta có

\(\left\{\begin{matrix}a+b+c\ge3\sqrt[3]{abc}\\a^2+b^2+c^2\ge3\sqrt[3]{\left(abc\right)^2}\end{matrix}\right.\)

\(=>\left(a+b+c\right)\left(a^2+b^2+c^2\right)\ge3\sqrt[3]{abc}.3\sqrt[3]{\left(abc\right)^2}\)

\(=>\left(a+b+c\right)\left(a^2+b^2+c^2\right)\ge9\sqrt[3]{\left(abc\right)^3}\)

\(=>\left(a+b+c\right)\left(a^2+b^2+c^2\right)\ge9abc\) (điều phải chứng minh )

Bài 1c) Ta có

\(\left(1+a\right)\left(1+b\right)\left(1+c\right)\ge\left(1+\sqrt[3]{abc}\right)^3\)

\(=>1+a+b\left(1+a\right)\left(1+c\right)\ge1^3+3.1^2.\sqrt[3]{abc}+3.1.\sqrt[3]{\left(abc\right)^2}+\sqrt[3]{\left(abc\right)^3}\)

\(=>\left(1+a+b+ab\right)\left(1+c\right)\ge1+3\sqrt[3]{abc}+3\sqrt[3]{\left(abc\right)^2}+abc\)

\(=>1+a+b+ab+c\left(1+a+b+ab\right)\ge1+3\sqrt[3]{abc}+3\sqrt[3]{\left(abc\right)^2}+abc\)

\(=>1+a+b+ab+c+ca+bc+abc\ge1+3\sqrt[3]{abc}+3\sqrt[3]{\left(abc\right)^2}+abc\)

\(=>a+b+c+ab+bc+ca\ge3\sqrt[3]{abc}+3\sqrt[3]{\left(abc\right)^2}\)

Áp dụng bất đẳng thức Cô-si bộ 3 số cho vế trái ta có

\(\left\{\begin{matrix}a+b+c\ge3\sqrt[3]{abc}\\ab+bc+ac\ge3\sqrt[3]{\left(abc\right)^2}\end{matrix}\right.\)

\(=>a+b+c+ab+bc+ac\ge3\sqrt[3]{abc}+3\sqrt[3]{\left(abc\right)^2}\) (điều phải chứng minh )

Bài 2a)

Áp dụng bất đẳng thức Cô-si cho từng cặp ta có

\(\left\{\begin{matrix}\frac{bc}{a}+\frac{ca}{b}\ge2\sqrt{\frac{bc}{a}.\frac{ca}{b}}=2\sqrt{c^2}=2c\\\frac{ca}{b}+\frac{ab}{c}\ge2\sqrt{\frac{ca}{b}.\frac{ab}{c}}=2\sqrt{a^2}=2a\\\frac{bc}{a}+\frac{ab}{c}\ge2\sqrt{\frac{bc}{a}.\frac{ab}{c}}=2\sqrt{b^2}=2b\end{matrix}\right.\)

\(=>2\left(\frac{bc}{a}+\frac{ca}{b}+\frac{ab}{c}\right)\ge2\left(a+b+c\right)\)

\(=>\frac{bc}{a}+\frac{ca}{b}+\frac{ab}{c}\ge a+b+c\) (điều phải chứng minh )

Bài 2b)

Chứng minh BĐT \(\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge9\)

Áp dụng BĐT Cô-si cho vế trái ta có

\(\left\{\begin{matrix}a+b+c\ge3\sqrt[3]{abc}\\\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge3\sqrt[3]{\frac{1}{abc}}\end{matrix}\right.\)

\(=>\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge3\sqrt[3]{abc}.3\sqrt[3]{\frac{1}{abc}}\)

\(=>\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge9.\sqrt[3]{\frac{abc}{abc}}\)

\(=>\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge9\) (điều phải chứng minh )

Ta có \(\frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b}\ge\frac{3}{2}\)

\(=>\frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b}+3\ge\frac{3}{2}+3\)

\(=>\frac{a}{b+c}+1+\frac{b}{a+c}+1+\frac{c}{a+b}+1\ge\frac{9}{2}\)

\(=>\frac{a+b+c}{b+c}+\frac{a+b+c}{a+c}+\frac{a+b+c}{a+b}\ge\frac{9}{2}\)

\(=>\left(a+b+c\right)\left(\frac{1}{b+c}+\frac{1}{a+c}+\frac{1}{a+b}\right)\ge\frac{9}{2}\)

\(=>2\left(a+b+c\right)\left(\frac{1}{b+c}+\frac{1}{a+c}+\frac{1}{a+b}\right)\ge9\)

Áp dụng BĐT vừa chứng minh \(\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge9\)

\(=>\left(b+c+a+c+a+b\right)\left(\frac{1}{b+c}+\frac{1}{a+c}+\frac{1}{a+b}\right)\ge9 \) (Điều phải chứng minh )

nhiều quá bạn à

b) \(\left(\dfrac{\sqrt{14}-\sqrt{7}}{1-\sqrt{2}}+\dfrac{\sqrt{15}-\sqrt{5}}{1-\sqrt{3}}\right):\dfrac{1}{\sqrt{7}-\sqrt{5}}\)

\(=\left(\dfrac{\sqrt{7}\left(\sqrt{2}-1\right)}{1-\sqrt{2}}+\dfrac{\sqrt{5}\left(\sqrt{3}-1\right)}{1-\sqrt{3}}\right).\left(\sqrt{7}-\sqrt{5}\right)\)

\(=\left(-\sqrt{7}-\sqrt{5}\right).\left(\sqrt{7}-\sqrt{5}\right)=-\left(\sqrt{7}+\sqrt{5}\right)\left(\sqrt{7}-\sqrt{5}\right)\)

\(=-\left(7-5\right)=-2\)

c) \(\dfrac{a\sqrt{b}+b\sqrt{a}}{\sqrt{ab}}:\dfrac{1}{\sqrt{a}-\sqrt{b}}=\dfrac{\sqrt{ab}\left(\sqrt{a}+\sqrt{b}\right)}{\sqrt{ab}}.\left(\sqrt{a}-\sqrt{b}\right)\)

\(=\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)=a-b\)

d) \(\left(1+\dfrac{a+\sqrt{a}}{\sqrt{a}+1}\right)\left(1-\dfrac{a-\sqrt{a}}{\sqrt{a}-1}\right)\)

\(=\left(1+\dfrac{\sqrt{a}\left(\sqrt{a}+1\right)}{\sqrt{a}+1}\right)\left(1-\dfrac{\sqrt{a}\left(\sqrt{a}-1\right)}{\sqrt{a}-1}\right)\)

\(=\left(1+\sqrt{a}\right)\left(1-\sqrt{a}\right)=1-a\)

b) \(\left(\dfrac{\sqrt{14}-\sqrt{7}}{1-\sqrt{2}}\dfrac{\sqrt{15}-\sqrt{5}}{1-\sqrt{3}}\right):\dfrac{1}{\sqrt{7}-\sqrt{5}}\)

\(=\left(\dfrac{\sqrt{7}\left(\sqrt{2}-1\right)}{1-\sqrt{2}}+\dfrac{\sqrt{5}\left(\sqrt{3}-1\right)}{1-\sqrt{3}}\right).\left(\sqrt{7}-\sqrt{5}\right)\)

\(=\left(-\sqrt{7}+\left(-\sqrt{5}\right)\right).\left(\sqrt{7}-\sqrt{5}\right)=-\left(\sqrt{7}+\sqrt{5}\right)\left(\sqrt{7}-\sqrt{5}\right)=-2\)

c)\(\dfrac{a\sqrt{b}+b\sqrt{a}}{\sqrt{ab}}:\dfrac{1}{\sqrt{a}-\sqrt{b}}=\dfrac{\sqrt{ab}\left(\sqrt{a}+\sqrt{b}\right)}{\sqrt{ab}}.\left(\sqrt{a}-\sqrt{b}\right)\)

\(=\left(\sqrt{a}+\sqrt{b}\right).\left(\sqrt{a}-\sqrt{b}\right)=a-b\)