một xe máy đi từ A đến B hết 3 giờ.1 xe đạp đi từ B về A hết 5 giờ.hỏi nếu cùng xuất phát cùng 1 lúc và đi ngược chiều nhau thì sau bao lâu 2 xe sẽ gặp nhau?
Bài 2: Dãy số
Để mình giúp ![]()
1 giờ xe máy đi đc:
\(1:3=\frac{1}{3}\) (quãng đường AB)
1 giờ xe đạp đi đc:
\(1:5=\frac{1}{5}\) (quãng đường AB)
1 giờ xe máy và xe đạp đi đc:
\(\frac{1}{3}+\frac{1}{5}=\frac{8}{15}\) (quãng đường AB)
Sau số giờ thì 2 xe gặp nhau là:
\(1:\frac{8}{15}=\frac{15}{8}\) (giờ)
Đổi:\(\frac{15}{8}h=1^o52'30'\)
Vậy sau 1 giờ 52 phút 30 giây thì 2 xe gặp nhau
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Rút gọn: a)6.9-2.17/63.3-119
b)3.7.13.37.39-10101/505050-70707.
Mình đang cần gấp.Các bạn làm ơn giúp mình
a) \(\frac{6.9-2.17}{63.3-119}=\frac{54-34}{189-119}=\frac{20}{70}=\frac{2}{7}\)
b)Mình làm ở đây rồi nhá: Câu hỏi của Lady Ice - Học và thi online với HOC24
Đúng 0
Bình luận (0)
Dùng định nghĩa tìm các giới hạn sau:a) ;b) .
Đọc tiếp
Dùng định nghĩa tìm các giới hạn sau:
a) ;
b) .
a) Hàm số f(x) = xác định trên R\{
} và ta có x = 4 ∈ (
;+∞).
Giả sử (xn) là dãy số bất kì và xn ∈ (;+∞); xn ≠ 4 và xn → 4 khi n → +∞.
Ta có lim f(xn) = lim =
=
.
Vậy
=
.
b) Hàm số f(x) = xác định trên R.
Giả sử (xn) là dãy số bất kì và xn → +∞ khi n → +∞.
Ta có lim f(xn) = lim = lim
= -5.
Vậy
= -5.
Đúng 0
Bình luận (0)
Tính các giới hạn sau:a) ;b) ;c) ;d) ;e) ;f) .
Đọc tiếp
Tính các giới hạn sau:
a)
;
b)
;
c)
;
d)
;
e)
;
f)
.
a)
=
= -4.
b)
=
=
(2-x) = 4.
c)
=
=
=
=
.
d)
=
= -2.
e)
= 0 vì
(x2 + 1) =
x2( 1 +
) = +∞.
f)
=
= -∞, vì
> 0 với ∀x>0.
Đúng 0
Bình luận (0)
Tính:a) (x4 – x2 + x - 1);b) (-2x3 + 3x2 -5 );c) ;d) .
Đọc tiếp
Tính:
a)  (x4 – x2 + x - 1);
(x4 – x2 + x - 1);
b)  (-2x3 + 3x2 -5 );
(-2x3 + 3x2 -5 );
c) 
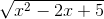 ;
;
d) 
 .
.
a)  (x4 – x2 + x - 1) =
(x4 – x2 + x - 1) =  x4(1 -
x4(1 - 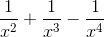 ) = +∞.
) = +∞.
b)  (-2x3 + 3x2 -5 ) =
(-2x3 + 3x2 -5 ) =  x3(-2 +
x3(-2 + 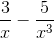 ) = +∞.
) = +∞.
c) 
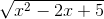 =
= 
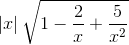 = +∞.
= +∞.
d) 
 =
= 

= 
 =
= 
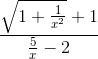 = -1.
= -1.
Đúng 0
Bình luận (0)
Một thấu kính hội tụ có tiêu cự là f. Gọi d và d lần lượt là khoảng cách từ một vật thật AB và từ ảnh AB của nó tới quang tâm O của thấu kính (h.54). Công thức thấu kính là a) Tìm biểu thức xác định hàm số d φ(d).b) Tìm φ(d), φ(d) và φ(d). Giải thích ý nghĩa của các kết quả tìm được.
Đọc tiếp
Một thấu kính hội tụ có tiêu cự là f. Gọi d và d' lần lượt là khoảng cách từ một vật thật AB và từ ảnh A'B' của nó tới quang tâm O của thấu kính (h.54). Công thức thấu kính là
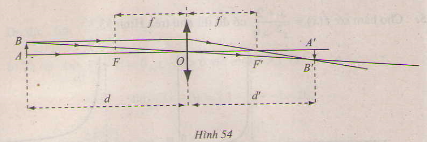
a) Tìm biểu thức xác định hàm số d' = φ(d).
b) Tìm φ(d),
φ(d) và
φ(d). Giải thích ý nghĩa của các kết quả tìm được.
a) Từ hệ thức suy ra d' = φ(d) =
.
b) +) φ(d) =
= +∞ .
Ý nghĩa: Nếu vật thật AB tiến dần về tiêu điểm F sao cho d luôn lớn hơn f thì ảnh của nó dần tới dương vô cực.
+) φ(d) =
= -∞.
Ý nghĩa: Nếu vật thật AB tiến dần về tiêu điểm F sao cho d luôn nhỏ hơn f thì ảnh của nó dần tới âm vô sực.
+) φ(d) =
=
= f.
Ý nghĩa: Nếu vật thật AB ở xa vô cực so với thấu kính thì ảnh của nó ở ngay trên tiêu diện ảnh (mặt phẳng qua tiêu điểm ảnh F' và vuông góc với trục chính).
Đúng 0
Bình luận (0)
Dùng định nghĩa xét tính liên tục của hàm số f(x) = x3 + 2x - 1 tại x0 = 3
Hàm số f(x) = x3 + 2x - 1 xác định trên R và x0 = 3 ∈ R.
f(x) =
(x3 + 2x - 1) = 33 + 2.3 - 1 = f(3)
nên hàm số đã cho liên tục tại điểm x0 = 3.
Đúng 0
Bình luận (0)
a) Xét tính liên tục của hàm số y g(x) tại x0 2, biết g(x) .b) Trong biểu thức xác định g(x) ở trên, cần thay số 5 bởi số nào để hàm số liên tục tại x0 2.
Đọc tiếp
a) Xét tính liên tục của hàm số y = g(x) tại x0 = 2, biết
g(x) = .
b) Trong biểu thức xác định g(x) ở trên, cần thay số 5 bởi số nào để hàm số liên tục tại x0 = 2.
a) Ta có g(x) =
=
(x2 + 2x + 4) = 22 +2.2 +4 = 12.
Vì g(x) ≠ g(2) nên hàm số y = g(x) gián đoạn tại x0 = 2.
b) Để hàm số y = f(x) liên tục tại x0 = 2 thì ta cần thay số 5 bởi số 12.
Đúng 0
Bình luận (0)
Ý kiến sau đúng hay sai ?
"Nếu hàm số y = f(x) liên tục tại điểm x0 còn hàm số y = g(x) không liên tục tại x0, thì
y = f(x) + g(x) là một hàm số không liên tục tại x0."
Ý kiến đúng
Giả sử ngược lại y = f(x) + g(x) liên tục tại x0. Đặt h(x) = f(x) + g(x). Ta có g(x) = h(x) - f(x).
Vì y = h(x) và y = f(x) liên tục tại x0 nên hiệu của chúng là hàm số y = g(x) phải liên tục tại x0. Điều này trái với giả thiết là y = g(x) không liên tục tại x0.
Đúng 0
Bình luận (0)
Cho hàm số f(x) và g(x) tanx + sin x.Với mỗi hàm số, hãy xác định các khoảng trên đó hàm số liên tục.
Đọc tiếp
Cho hàm số f(x) = và g(x) = tanx + sin x.
Với mỗi hàm số, hãy xác định các khoảng trên đó hàm số liên tục.
+) Hàm số f(x) = xác định khi và chỉ khi x2+ x - 6 ≠ 0 <=> x ≠ -3 và x ≠ 2.
Hàm số f(x) liên tục trên các khoảng (-∞; -3), (-3; 2) và (2; +∞)
+) Hàm số g(x) = tanx + sinx xác định khi và chỉ khi
tanx ≠ 0 <=> x ≠ +kπ với k ∈ Z.
Hàm số g(x) liên tục trên các khoảng ( - +kπ;
+kπ) với k ∈ Z.
Đúng 0
Bình luận (0)






