(d) y=-2+3x ,(d') y=mx+n . xđ m, n để (d) //(d') đi qua A(-1,2)

Những câu hỏi liên quan
Tìm m, n để đường thẳng mx – 2y = n đi qua điểm A(2;1) và giao điểm của hai đường thẳng (d1): x – 2y = 1, (d2): –3x + y = 7.
gọi giao điểm của 2 đường thẳng (d1) và (d2) là M(x1,y1)
Tọa độ giao điểm của đt (d1) và (d2) là nghiệm của hệ phương trình(hpt):
\(\left\{{}\begin{matrix}x_1-2y_1=1\\-3x_1+y_1=7\end{matrix}\right.< =>\left\{{}\begin{matrix}x_1=-3\\y_1=-2\end{matrix}\right.\) <=> M(-3;-2)
Vì đường thẳng mx-2y=n đi qua điểm A(2;1) và giao điểm của 2 đường thẳng trên nên ta có hpt:
\(\left\{{}\begin{matrix}2m-2=n\\-3m+4=n\end{matrix}\right.< =>^{ }\left\{{}\begin{matrix}m=\frac{6}{5}\\n=\frac{2}{5}\end{matrix}\right.\)
Vậy....
Tìm m và n để (d): y = mx + n đi qua 2 điểm A(2; 7) và B (1;3)
Thay tọa độ A và B vào pt d ta được:
\(\left\{{}\begin{matrix}2m+n=7\\1.m+n=3\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m=4\\n=-1\end{matrix}\right.\)
Đúng 1
Bình luận (0)
cho parabol (P): \(y=\dfrac{1}{4}x^{2}\) và đường thẳng (d): y=mx+n. Tìm giá trị của m,n để (d) đi qua điểm A(-1;-2) và tiếp xúc với (P)
Lời giải:
Để $(d)$ đi qua $A(-1;-2)$ thì: $-2=-m+n(1)$
Để $(d)$ và $(P)$ tiếp xúc nhau thì PT hoành độ giao điểm:
$\frac{1}{4}x^2-mx-n=0$ có nghiệm duy nhất
Điều này xảy ra khi:
$\Delta=m^2+n=0(2)$
Từ $(1);(2)\Rightarrow m=1$ hoặc $m=-2$
Nếu $m=1$ thì $n=-1$
Nếu $m=-2$ thì $n=-4$
Vậy............
Đúng 1
Bình luận (0)
Cho hàm số bậc nhất y=(m-3)x+5.Tìm m để dths đi qua A(-5,1)
Bài 2: cho đồ thị y=2x-mx+1.Tìm m để đt d đi qua N(-4,-3)
Xem chi tiết
Đường thẳng y = ( m -3 ).x + 5 đi qua A(-5;1)
=> A(-5;1) thuộc hàm số y = ( m - 3 ).x + 5
1 = ( m - 3).(-5) + 5
1 = -5m + 15 + 5
1 = -5m + 20
-5m = -19
m = 19/5
Vậy m = 19/5 thì y = ( m - 3)x + 5 đi qua A(-5;1)
bài 1 : cho (p):y-dfrac{x^2}{4} và (d) :y x+m
a, xđ m để (p) (d) cắt nhau tại hai điểm phân biệt A,B
b, xđ pt đt (d) song song với đt (d) và cắt (P) tại điểm có tung độ bằng -4
c, xđ phương trình đường thẳng (d)vuông góc với (d) và đi qua giao điểm của (d) và (p)
bài 2 : cho (p) y2x2
a, tìm hoành độ giao điểm cua (p) với đường thẳng y3x-1
b, tìm tọa độ giao điểm của (p) với đường thẳng ydfrac{6x-9}{2}
c, tìm giá trị của a,b sao cho đường thẳng yax+b tiếp xúc với (p) vad đi qua A(0;-2)
Đọc tiếp
bài 1 : cho (p):y=\(-\dfrac{x^2}{4}\) và (d) :y= \(x+m\)
a, xđ m để (p) (d) cắt nhau tại hai điểm phân biệt A,B
b, xđ pt đt (d') song song với đt (d) và cắt (P) tại điểm có tung độ bằng -4
c, xđ phương trình đường thẳng (d'')vuông góc với (d') và đi qua giao điểm của (d') và (p)
bài 2 : cho (p) y=2x2
a, tìm hoành độ giao điểm cua (p) với đường thẳng y=3x-1
b, tìm tọa độ giao điểm của (p) với đường thẳng y=\(\dfrac{6x-9}{2}\)
c, tìm giá trị của a,b sao cho đường thẳng y=ax+b tiếp xúc với (p) vad đi qua A(0;-2)
Bài 2:
a: PTHĐGĐ là:
\(2x^2-3x+1=0\)
=>(2x-1)(x-1)=0
=>x=1 hoặc x=1/2
b: PTHĐGĐ là:
\(2x^2-\dfrac{6x-9}{2}=0\)
\(\Leftrightarrow4x^2-6x+9=0\)
\(\text{Δ}=\left(-6\right)^2-4\cdot4\cdot9=36-16\cdot9=-108< 0\)
Do đó: PTVN
Đúng 0
Bình luận (0)
Cho hàm số bậc nhất : y (2m+1)x + m - 3 (d)
Xđ m để :
a ) (d) đi qua gốc tọa độ
b) (d) đi qua điểm A(-1;3)
c) (d) // y -x + 1
d) (d) cắt trục tung tại điểm có tung độ -1
e) (d) cắt đt y 2x + 3 tại 1 điểm trên trục tung
f) (d) cắt trục hoành tại điểm có hoành độ bằng 2
g) (d) cắt đt y x+3 tại 1 điểm trên trục hoành
h) Tìm 1 điểm cố định (d) luôn luôn đi qua vs forall m
Đọc tiếp
Cho hàm số bậc nhất : y = (2m+1)x + m - 3 (d)
Xđ m để :
a ) (d) đi qua gốc tọa độ
b) (d) đi qua điểm A(-1;3)
c) (d) // y = -x + 1
d) (d) cắt trục tung tại điểm có tung độ = -1
e) (d) cắt đt y = 2x + 3 tại 1 điểm trên trục tung
f) (d) cắt trục hoành tại điểm có hoành độ bằng 2
g) (d) cắt đt y = x+3 tại 1 điểm trên trục hoành
h) Tìm 1 điểm cố định (d) luôn luôn đi qua vs \(\forall m\)
cho đường thẳng (d) có phương trình: x(m+2)+(m-3)y=m-8
a) XĐ m để đường thẳng (d) luôn đi qua điểm P(-1;1)
b) CMR khi m thay đổi thì đường thẳng (d) luôn luôn đi qua 1 điểm cố định
Cho hàm số y=mx+3 (d) (m là hai số , m khác 0)
a) tìm m để đg thẳng (d) đi qua A (-2;7)
b)tìm m để đg thẳng (d) song song vs đồ thị hàm số y=2-3x
a) Để đồ thị đi qua A(-2,7) thì
.-2m+3=7
----> 2m=4
--->m=2
b) Để d) song song vs đồ thị y=2-3x thì
\(\left\{{}\begin{matrix}m=-3\\3\ne2\left(hn\right)\end{matrix}\right.\)
Vậy...
Cho hai đường thẳng (d) y = (2m – 3)x + n – 1 và (d') y = mx + 2n
Xác định các hệ số m, n sao cho:
b) (d) đi qua điểm A (2; 5) và B ( -2; 3)
b) (d) đi qua điểm A (2; 5) và B ( -2; 3) khi:
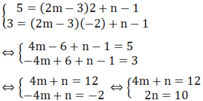
Đúng 0
Bình luận (1)





















