giải hệ phương trình {2a+3b=c
{a+15b=c
Giải phương trình: \(\dfrac{2a-3b}{x-2a}+\dfrac{3b-2a}{x-3b}=0\) ( a và b là hằng)
Sửa lại đề bài là giải PT và biện luận nhé các bạn
cho hệ phương trình (m - 1)x + y = m
x + ( m - 1)y = 2
a) giải hệ pt khi m = 3
b) tìm giá trị của m thỏa mãn \(2x^2 - 7y = 1 \)
c) tìm các giá trị của m để biểu thức \(\dfrac{2x-3y}{x+y}\) nhận giá trị nguyên
Thao m =3 và HPT ta có:
\(\left\{{}\begin{matrix}\left(3-1\right)x+y=3\\x+\left(3-1\right)y=2\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}2x+y=3\\x+2y=2\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}4x+2y=6\\x+2y=2\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}4x+2y=6\\3x=4\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}x=\dfrac{4}{3}\\y=\dfrac{1}{3}\end{matrix}\right.\)
Vậy với m=3 thì HPT có nghiệm (x;y) = (\(\dfrac{4}{3};\dfrac{1}{3}\))
a) Thay m=3 vào hệ phương trình, ta được:
\(\left\{{}\begin{matrix}2x+y=3\\x+2y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+y=3\\2x+4y=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-3y=-1\\2x+y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{1}{3}\\2x=3-y=3-\dfrac{1}{3}=\dfrac{8}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{4}{3}\\y=\dfrac{1}{3}\end{matrix}\right.\)
Vậy: Khi m=3 thì hệ phương trình có nghiệm duy nhất là \(\left\{{}\begin{matrix}x=\dfrac{4}{3}\\y=\dfrac{1}{3}\end{matrix}\right.\)
b) \(\left\{{}\begin{matrix}\left(m-1\right)x+y=m\\x+\left(m-1\right)y=2\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}x=2-\left(m-1\right)y\\\left(m-1\right)\left(2-\left(m-1\right)y\right)+y=m\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}x=2-my+y\\\left(m-1\right)\left(2-my+y\right)+y=m\left(1\right)\end{matrix}\right.\)
Từ (1) ta có:
\(\left(m-1\right)\left(2-my+y\right)=y=m\)
⇔\(2m-m^2y+my-2+my-y+y=m\)
⇔\(-m^2y+2my=-2m+2+m\)
⇔\(my\left(-m+2\right)=-2m+2+m\) (2)
Trường hợp 1:
\(-m+2=0\)
⇔m= \(\mp\)2
*Thay m=2 vào (2) ta có: 0y=0 ⇒m=2 (chọn)
*Thay m=-2 và (2) ta có: 0y= -4 ⇒m= -2 (loại)
Trường hợp 2:
-m+2 \(\ne0\)
⇔m\(\ne\) 2
⇒HPT có nghiệm duy nhất:
\(my=\dfrac{-2m+2+m}{-m+2}\)
⇒\(y=\dfrac{-2m+2+m}{-m+2}.\dfrac{1}{m}\)
⇒\(y=\dfrac{-2m+2+m}{-m^2+2m}\)
⇒\(x=2-m.\dfrac{-2m+2+m}{-m^2+2m}+\dfrac{-2m+2+m}{-m^2+2m}\)
Theo bài ra ta có:
\(2x^2-7y=1\)
⇔\(2.\left(2-m.\dfrac{-2m+2+m}{-m^2+2m}+\dfrac{-2m+2+m}{-m^2+2m}\right)^2-7\left(\dfrac{-2m+2+m}{-m^2+2m}\right)=1\)
\(2.\left(2-\dfrac{2m^2-2m-m^2}{-m^2+2m}+\dfrac{-2m+2+m}{-m^2+2m}\right)^2-\dfrac{14m-14-7m}{-m^2+2m}=1\)
Có gì bạn giải nốt nha, phương trình cũng "đơn giản" rồi ![]()
Mình bấm máy tính Casio nó ra kết quả m=1
nên với m =1 thì Thỏa mãn yêu cầu đề bài
:))))))))))
Giải hệ phương trình :
\(\left\{{}\begin{matrix}a+2b+3c=10\\2a+3b+c=13\\3a+b+2c=13\end{matrix}\right.\)
Bấm máy tính Casio fx-570 VN giải hệ phương trình 3 ẩn
Mode\(\rightarrow\) 5\(\rightarrow\) 2 :
| Hệ số | a | b | c | d |
| PT 1 | 1 | 2 | 3 | 10 |
| PT 2 | 2 | 3 | 1 | 13 |
| PT 3 | 3 | 1 | 2 | 13 |
Ấn dấu = ta được a=3, b=2, c=1 (trên màn hình máy tính là x,y,z)
2 Pt đầu khử a ,2 pt sau khử a ,ta được HPT 2 ẩn b,c
Cho hệ phương trình {4x-3y=6
{-5x+ay=8
a) Giải hệ phương trình với a=3
b) Tìm a để hệ phương trình có nghiệm âm duy nhất
a) Thay a=3 vào hệ pt, ta được:
\(\left\{{}\begin{matrix}4x-3y=6\\-5x+3y=8\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-x=14\\4x-3y=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-14\\-56-3y=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-14\\-3y=62\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-14\\y=-\dfrac{62}{3}\end{matrix}\right.\)
Vậy: Khi a=3 thì hệ pt có nghiệm duy nhất là: \(\left(x,y\right)=\left(-14;-\dfrac{62}{3}\right)\)
a. với a=3 ta có hpt: {4x-3y=6 {-5x+3y=8
<=> {-x=14 <=> {x=-14 {-5x+3y=8 {x= -62/3
Giả sử đường thẳng d có phương trình là ax + by + c = 0
Điều kiện a2 + b2 ≠ 0
d (A; d) = 2 ⇒ \(\dfrac{\left|a+b+c\right|}{\sqrt{a^2+b^2}}=2\)
d (B; d) = 4 ⇒ \(\dfrac{\left|2a+3b+c\right|}{\sqrt{a^2+b^2}}=4\)
Vậy |2a + 3b + c| = |2a + 2b + 2c|
⇔ \(\left[{}\begin{matrix}b=c\left(1\right)\\4a+5b+3c=0\left(2\right)\end{matrix}\right.\)
Từ (1) ⇒ (a + 2b)2 = 4 (a2 + b2)
⇒ \(\left[{}\begin{matrix}a=0\\3a=4b\end{matrix}\right.\)
Với a = 0 , chọn b = 1 => c = 1
=> Pt d : y + 1 = 0
Với 3a = 4b, chọn a = gì tùy => b => c
=> d
(2) => (cái này vô lí)
cho hệ phương trình 2x+y=8,4x+my=2m+18
a) Tim m để hệ phương trình có nghiệm duy nhất.
b) Tim m nguyên để hệ phương trình có nghiệm duy nhất là các số nguyên.
c giả sử x=a,y=b là nghiệm duy nhất của hệ.tìm m để 2a-3b>0
Giải hệ phương trình x + 3 y = 1 a 2 + 1 x + 6 y = 2 a trong mỗi trường hợp sau:
a) a = -1; b) a = 0; c) a = 1.
Cách 1
Ta có: 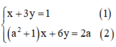
Từ (1) rút ra được x = 1 – 3y (*)
Thay vào phương trình (2) ta được :
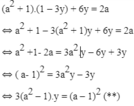
a) a = -1, phương trình (**) trở thành : 0y = 4
Phương trình trên vô nghiệm
Vậy hệ phương trình khi a = -1 vô nghiệm.
b) a = 0, phương trình (**) trở thành -3y = 1 ⇔
Thay 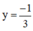 vào (*) ta được x = 2.
vào (*) ta được x = 2.
Vậy hệ phương trình khi a = 0 có nghiệm duy nhất 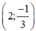
c) a = 1, phương trình (**) trở thành: 0y = 0
Phương trình nghiệm đúng với mọi y.
Vậy hệ phương trình khi a = 1 có vô số nghiệm dạng (1 – 3y; y) (y ∈ R).
Cách 2
a) Thay a = -1 vào hệ phương trình ta được hệ phương trình mới:

Vậy hệ phương trình vô nghiệm khi a= - 1.
b) Thay a = 0 vào hệ phương trình ta được hệ phương trình mới:

c) Thay a=1 vào hệ phương trình ta được hệ phương trình mới:
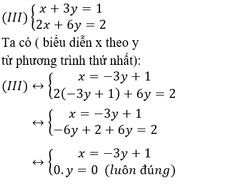
Vậy với a= 1 hệ phương trình có vô số nghiệm với nghiệm tổng quát là (-3y+1;y),(y ∈ R)
Kiến thức áp dụng
+ Giải hệ phương trình 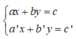 ta làm như sau:
ta làm như sau:
Bước 1: Từ một phương trình (coi là phương trình thứ nhất), ta biểu diễn x theo y (hoặc y theo x) ta được phương trình (*). Sau đó, ta thế (*) vào phương trình thứ hai để được một phương trình mới ( chỉ còn một ẩn).
Bước 2: Dùng phương trình mới ấy thay thế cho phương trình thứ hai, phương trình (*) thay thế cho phương trình thứ nhất của hệ ta được hệ phương trình mới tương đương .
Bước 3: Giải hệ phương trình mới ta tìm được nghiệm của hệ phương trình.
+ Nếu xuất hiện phương trình dạng 0x = a (hoặc 0y = a) thì ta kết luận hệ phương trình vô nghiệm nếu a ≠ 0 hoặc hệ có vô số nghiệm nếu a = 0.
Bài 1: Cho hệ phương trình: \(\hept{\begin{cases}x+y=2a-1\\x^2+y^2=a^2+2a-3\end{cases}}\)
Giả sử (x; y) là nghiệm của hệ phương trình. Xác định a để xy đạt GTNN. Tìm GTNN đó.
Bài 2: Giải hệ phương trình: \(\hept{\begin{cases}\left(c+a\right)y+\left(a+b\right)z-\left(b+c\right)x=2a^3\\\left(a+b\right)z+\left(b+c\right)x-\left(c+a\right)y=2b^3\\\left(b+c\right)x+\left(c+a\right)y-\left(a+b\right)z=2c^3\end{cases}}\)
Đặt S=x+y, P=x.y
Ta có:S=2a-1, x^2+y^2=S^2-2P=a^2+2a-3
\Rightarrow P=\frac{1}{2}[(2a-1)^2-(a^2+2a-3)]=\frac{1}{2}(3a^2-6a+4)
Trước hết tìm a để hệ có nghiệm.
Điều kiện để hệ có nghiệm:S^2-4P \geq 0 \Leftrightarrow (2a-1)^2-2(3a^2-6a+4)\geq 0
\Leftrightarrow -2a^2+8a-7 \geq 0 \leftrightarrow 2-\frac{\sqrt{2}}{2} \leq a \leq 2+\frac{\sqrt{2}}{2} (1)
Tìm a để P=\frac{1}{2}(3a^2-6a+4) đạt giá trị nhỏ nhất trên đoạn
[2-\frac{\sqrt{2}}{2} ;2+\frac{\sqrt{2}}{2}]
Ta có hoành độ đỉnh a_0=\frac{6}{2.3}=1Parabol có bề lõm quay lên do đó \min P=P(2-\frac{\sqrt{2}}{2} )$
Vậy với a=2-\frac{\sqrt{2}}{2} thì xy đạt giá trị nhỏ nhất.
Giải hệ phương trình \(\left\{{}\begin{matrix}2a^3+2a+b^3-3b=62\\a^2+b^2-2a+2b=2\end{matrix}\right.\)
Đây nha bạn trọng :)  :)
:)