Cho đường tròn (O, R), từ điểm A nằm ngoài đường tròn (O) vẽ hai tiếp tuyến AB, AC với (O) (B, C lần lượt là các tiếp điểm)
a, C/m ABOC là tứ giác nội tiếp
b, Gọi D là trung điểm của AC, BD cắt đường tròn tại E, đường thẳng AE cắt đường tròn (O) tại điểm thứ hai là F. C/m AB²= AE. AF
c, C/m BC=CF










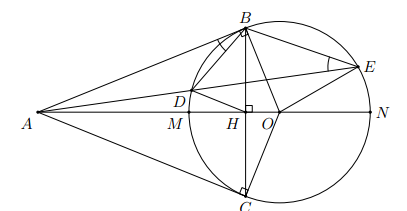 hình
hình














